
Skillnad mellan en vanlig bråk och ett decimaltal
Att identifiera vad är skillnaden mellan en vanlig bråk och ett decimaltal det räcker att observera båda elementen: det ena representerar ett rationellt tal och det andra inkluderar i sin konstitution en hel del och en decimaldel.
En "vanlig bråkdel" är uttrycket för en kvantitet dividerad med en annan utan att utföra nämnda delning. Matematiskt är en vanlig bråk ett rationellt tal, som definieras som kvoten av två heltal "a / b", där b ≠ 0.

Ett "decimaltal" är ett tal som består av två delar: ett heltal och en decimaldel..
För att separera heltalets del från decimaldelen placeras ett komma, kallat decimalpunkt, även om en period också används beroende på bibliografin.
Decimaltal
Ett decimaltal kan ha ett ändligt eller oändligt antal i sin decimaldel. Det oändliga antalet decimaler kan också sönderdelas i två typer:
Periodisk
Det vill säga den har ett upprepande mönster. Till exempel 2.454545454545…
Inte periodiskt
De har inget upprepande mönster. Till exempel 1.7845265397219 ...
Tal som har ett periodiskt oändligt eller oändligt antal decimaler kallas rationella tal, medan de som har ett icke-periodiskt oändligt antal kallas irrationella.
Föreningen av uppsättningen rationella tal och uppsättningen irrationella tal är känd som uppsättningen av reella tal.

Skillnader mellan vanlig bråk och decimaltal
Skillnaderna mellan en vanlig bråk och ett decimaltal är:
1-decimal
Varje vanlig bråk har ett ändligt antal siffror i sin decimaldel eller ett oändligt periodiskt nummer, medan ett decimaltal kan ha ett oändligt icke-periodiskt antal nummer i sin decimaldel..
Ovanstående säger att varje rationellt tal (varje vanlig bråk) är ett decimaltal, men inte varje decimaltal är ett rationellt tal (en gemensam bråk).
2- Notation
Varje vanlig bråk betecknas som kvoten av två heltal, medan ett irrationellt decimaltal inte kan betecknas på detta sätt..
De mest använda irrationella decimaltalen i matematik betecknas med kvadratrötter (√ ), kubisk (³√ ) och högre betyg.
Förutom dessa finns det två mycket berömda nummer, som är Eulernumret, betecknat med e; och siffran pi, betecknad med π.

Hur man går från en vanlig bråk till ett decimaltal?
För att gå från en vanlig bråk till ett decimaltal gör du bara motsvarande uppdelning. Om du till exempel har 3/4 är motsvarande decimaltal 0,75.
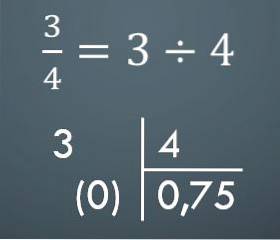
Hur man går från ett rationellt decimaltal till en vanlig bråkdel?
Den omvända processen till den tidigare kan också göras. Följande exempel illustrerar en teknik för att flytta från ett rationellt decimaltal till en vanlig bråkdel:
- Låt x = 1,78
Eftersom x har två decimaler multipliceras den tidigare likheten med 10² = 100, med vilken vi får 100x = 178; och lösa för x det resulterar i att x = 178/100. Det sista uttrycket är den vanliga fraktionen som representerar siffran 1,78.
Men kan denna process göras för siffror med ett periodiskt oändligt antal decimaler? Svaret är ja, och följande exempel visar stegen att följa:
- Låt x = 2.193193193193 ...
Eftersom perioden med detta decimaltal har tre siffror (193) multipliceras det föregående uttrycket med 10³ = 1000, med vilket vi får uttrycket 1000x = 2193.193193193193 ... .
Nu subtraheras det sista uttrycket från det första och hela decimaldelen avbryts och lämnar uttrycket 999x = 2191, från vilket vi får att den gemensamma fraktionen är x = 2191/999.
Referenser
- Anderson, J. G. (1983). Teknisk matematik (Illustrerad utgåva). Industrial Press Inc..
- Avendaño, J. (1884). Komplett handbok för grundläggande och högre grundinstruktioner: för användning av blivande lärare och särskilt studenter från de normala skolorna i provinsen (2 utgåva, Vol. 1). Utskrift av D. Dionisio Hidalgo.
- Coates, G. och. (1833). Den argentinska aritmetiken: Komplett avhandling om praktisk aritmetik. För användning av skolor. Skriva ut av staten.
- Från havet. (1962). Matematik för workshopen. Återvänd.
- DeVore, R. (2004). Praktiska problem i matematik för värme- och kyltekniker (Illustrerad utgåva). Cengage Learning.
- Jariez, J. (1859). Fullständig kurs i fysiska och mekaniska matematiska vetenskaper tillämpad på industriell konst (2 utgåva). Järnväg tryckeri.
- Palmer, C. I., & Bibb, S. F. (1979). Praktisk matematik: aritmetik, algebra, geometri, trigonometri och glidregel (omtryck ed.). Återvänd.



Ingen har kommenterat den här artikeln än.