
Linjär utvidgning vad är det, formel och koefficienter, exempel
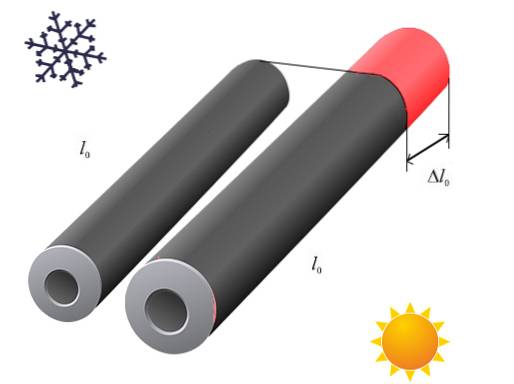
De linjär utvidgning inträffar när ett objekt upplever expansion på grund av en variation i temperaturen, främst i en dimension. Detta beror på materialets egenskaper eller dess geometriska form..
Till exempel i en tråd eller en stång, när det sker en temperaturökning, är det längden som drabbas störst på grund av termisk expansion..

Kablarna som fåglarna i den föregående figuren sitter på sträcker sig när temperaturen ökar; istället drar de sig ihop när de svalnar. Detsamma händer till exempel med stängerna som utgör järnvägsspåren.
Artikelindex
- 1 Vad är linjär utvidgning??
- 2 Formel för linjär utvidgning och dess koefficient
- 2.1 Koefficient för linjär expansion för olika material
- 3 fungerade exempel på linjär expansion
- 3.1 Exempel 1
- 3.2 Exempel 2
- 3.3 Exempel 3
- 3.4 Exempel 4
- 4 Referenser
Vad är linjär utvidgning??
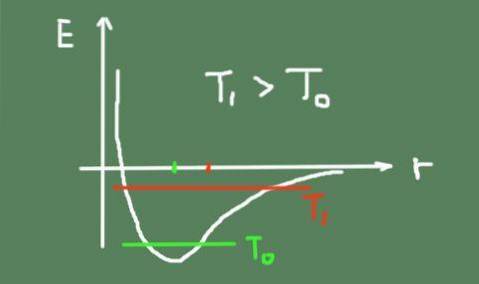
I ett fast material bibehåller atomerna sina relativa positioner mer eller mindre fixerade runt en jämviktspunkt. Men på grund av termisk omrörning oscillerar de alltid runt samma.
När temperaturen ökar ökar också den termiska svängningen, vilket gör att mellersta svängningspositioner ändras. Detta beror på att bindningspotentialen inte är exakt parabolisk och har asymmetri runt det minsta.
Nedan är en figur som beskriver den kemiska bindningsenergin som en funktion av det interatomära avståndet. Det visar också den totala svängningsenergin vid två temperaturer och hur svängningens centrum rör sig.
Formel för linjär utvidgning och dess koefficient
För att mäta linjär expansion börjar vi med en initial längd L och en initial temperatur T för objektet vars expansion ska mätas..
Antag att detta objekt är en stapel vars längd är L och tvärsnittsdimensionerna är mycket mindre än L.
Detta objekt utsätts först för en temperaturvariation AT, så att den slutliga temperaturen för objektet när den termiska jämvikten med värmekällan har fastställts blir T '= T + AT.
Under denna process kommer objektets längd också att ändras till ett nytt värde L '= L + ΔL, där ΔL är variationen i längden.
Koefficienten för linjär expansion α definieras som kvoten mellan den relativa längdvariationen per enhetsvariation i temperaturen. Följande formel definierar koefficienten för linjär expansion a:
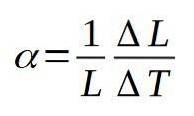
Dimensionerna för koefficienten för linjär expansion är de för temperaturens inversa.
Koefficient för linjär expansion för olika material
Därefter ger vi en lista över koefficienten för linjär expansion för några typiska material och element. Koefficienten beräknas vid normalt atmosfärstryck baserat på en omgivningstemperatur på 25 ° C; och dess värde anses vara konstant i ett AT-intervall upp till 100 ° C.
Enheten för linjär expansionskoefficient kommer att vara (° C)-1.
- Stål: α = 12 ∙ 10-6 (° C)-1
- Aluminium: α = 23 ∙ 10-6 (° C)-1
- Guld: α = 14 ∙ 10-6 (° C)-1
- Koppar: α = 17 ∙ 10-6 (° C)-1
- Mässing: α = 18 ∙ 10-6 (° C)-1
- Järn: α = 12 ∙ 10-6 (° C)-1
- Glas: α = (7 till 9) ∙ 10-6 (° C)-1
- Kvicksilver: α = 60,4 ∙ 10-6 (° C)-1
- Kvarts: α = 0,4 ∙ 10-6 (° C)-1
- Diamant: α = 1,2 ∙ 10-6 (° C)-1
- Bly: α = 30 ∙ 10-6 (° C)-1
- Ek: α = 54 ∙ 10-6 (° C)-1
- PVC: α = 52 ∙ 10-6 (° C)-1
- Kolfiber: α = -0,8 ∙ 10-6 (° C)-1
- Betong: α = (8 till 12) ∙ 10-6 (° C)-1
De flesta material sträcker sig med en ökning av temperaturen. Vissa speciella material som kolfiber krymper dock med ökande temperatur..
Arbetade exempel på linjär utvidgning
Exempel 1
En kopparkabel hängs mellan två stolpar och längden på en sval dag vid 20 ° C är 12 m. Beräkna värdet på dess längd på en varm dag vid 35 ° C.
Lösning
Med utgångspunkt från definitionen av koefficienten för linjär expansion, och att veta att för koppar är denna koefficient lika med: α = 17 ∙ 10-6 (° C)-1
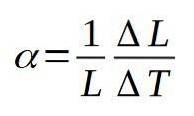
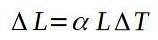
Kopparkabeln genomgår en längdökning, men den är bara 3 mm. Det vill säga kabeln går från att ha 12 000 m till att ha 12 003 m.
Exempel 2
I en smedja går en aluminiumstång ut från ugnen vid 800 grader Celsius och mäter en längd på 10,00 m. När den svalnat till rumstemperaturen på 18 grader Celsius, bestämma hur lång baren kommer att vara.
Lösning
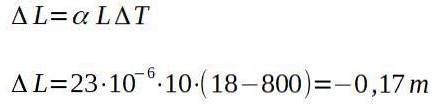
Med andra ord kommer baren, när den är kall, en total längd på:
9,83 m.
Exempel 3
En stålnit har en diameter på 0,915 cm. På en aluminiumplatta görs ett hål på 0,910 cm. Dessa är de initiala diametrarna när omgivningstemperaturen är 18 ° C.
Till vilken minimitemperatur måste plattan värmas upp för att niten ska passera genom hålet? Målet med detta är att när järnet återgår till rumstemperatur kommer niten att vara tätt i plattan.
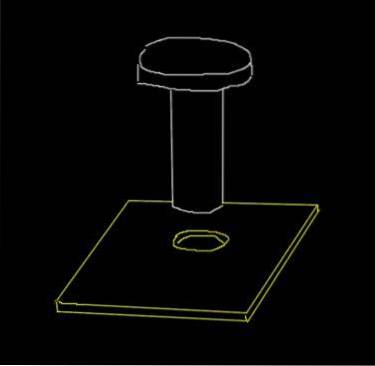
Lösning
Även om plattan är en yta är vi intresserade av utvidgningen av hålets diameter, vilket är en endimensionell kvantitet..
Låt oss ringa D0 till den ursprungliga diametern på aluminiumplattan och D till vilken den en gång kommer att värmas upp.
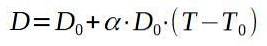
För att lösa den slutliga temperaturen T har vi:
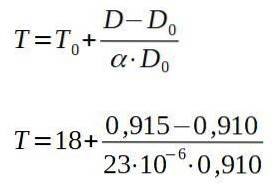
Resultatet av de tidigare operationerna är 257 ° C, vilket är den lägsta temperatur som plattan måste värmas upp så att niten passerar genom hålet.
Exempel 4
Niten och plattan från föregående övning placeras tillsammans i en ugn. Bestäm vilken minimitemperatur ugnen måste ha för att stålniten ska passera genom hålet i aluminiumplattan.
Lösning
I det här fallet utvidgas både niten och hålet. Men stålets expansionskoefficient är α = 12 ∙ 10-6 (° C)-1, medan aluminium är α = 23 ∙ 10-6 (° C)-1 .
Vi letar sedan efter en slutlig temperatur T så att båda diametrarna sammanfaller.
Om vi kallar niten 1 och aluminiumplattan 2 letar vi efter en slutlig temperatur T så att D1 = Dtvå.
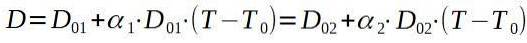
Om vi löser den slutliga temperaturen T sitter vi kvar med:
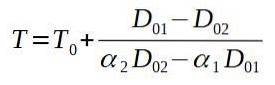
Sedan sätter vi motsvarande värden.
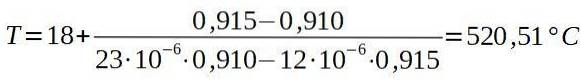
Slutsatsen är att ugnen måste vara minst 520,5 ° C för att niten ska passera genom hålet i aluminiumplattan.
Referenser
- Giancoli, D. 2006. Fysik: principer med tillämpningar. Sjätte upplagan. Prentice Hall. 238-249.
- Bauer, W. 2011. Fysik för teknik och vetenskap. Volym 1. Mac Graw Hill. 422-527.


Ingen har kommenterat den här artikeln än.