
Normal fördelningsformel, egenskaper, exempel, träning

De normal distribution eller Gaussisk fördelning är sannolikhetsfördelningen i en kontinuerlig variabel, i vilken sannolikhetsdensitetsfunktionen beskrivs av en exponentiell funktion av kvadratisk och negativ argument, vilket ger upphov till en klockform.
Namnet på normalfördelning kommer från det faktum att denna fördelning är den som gäller för det största antalet situationer där någon kontinuerlig slumpmässig variabel är involverad i en given grupp eller population..
Exempel där normalfördelningen tillämpas är: höjden på män eller kvinnor, variationer i måttet av viss fysisk storlek eller i mätbara psykologiska eller sociologiska egenskaper som den intellektuella kvoten eller konsumtionsvanorna för en viss produkt.
Å andra sidan kallas det en Gaussisk fördelning eller Gaussisk klocka, för det är detta tyska matematiska geni som krediteras sin upptäckt för den användning han gav den för att beskriva det statistiska felet i astronomiska mätningar redan år 1800..
Det sägs emellertid att denna statistiska distribution tidigare publicerades av en annan stor matematiker av fransk ursprung, som Abraham de Moivre, redan 1733.
Artikelindex
- 1 Formel
- 2 Kännetecken för normalfördelningen
- 2.1 Konfidensintervall
- 3 Tillämpningar av normalfördelningen
- 4 Exempel
- 5 Övningen löst
- 6 Referenser
Formel
Till normalfördelningsfunktionen i den kontinuerliga variabeln x, med parametrar μ Y σ det betecknas med:
N (x; μ, σ)
och det är uttryckligen skrivet så här:
N (x; μ, σ) = ∫-∞x f (s; μ, σ) ds
var f (u; μ, σ) är sannolikhetsdensitetsfunktionen:
f (s; μ, σ) = (1 / (σ√ (2π)) Exp (- stvå/ (2σtvå))
Konstanten som multiplicerar den exponentiella funktionen i sannolikhetsdensitetsfunktionen kallas normaliseringskonstanten och den har valts på ett sådant sätt att:
N (+ ∞, μ, σ) = 1
Det tidigare uttrycket säkerställer att sannolikheten för att den slumpmässiga variabeln x är mellan -∞ och + ∞ är 1, det vill säga 100% sannolikhet.
Parameter μ är det aritmetiska medelvärdet för den kontinuerliga slumpmässiga variabeln x y σ standardavvikelsen eller kvadratroten av variansen för samma variabel. I händelse av att μ = 0 Y σ = 1 vi har då standardnormalfördelningen eller den normala normalfördelningen:
N (x; μ = 0, σ = 1)
Kännetecken för normalfördelningen
1 - Om en slumpmässig statistisk variabel följer en normal fördelning av sannolikhetstätheten f (s; μ, σ), de flesta uppgifterna är grupperade kring medelvärdet μ och är utspridda kring det på ett sådant sätt att drygt ⅔ av datan är mellan μ - σ Y μ + σ.
2- Standardavvikelsen σ det är alltid positivt.
3- Formen för densitetsfunktionen F liknar en klocka, varför denna funktion ofta kallas en Gaussisk klocka eller Gaussisk funktion.
4- I en Gaussisk fördelning sammanfaller medelvärdet, medianen och läget.
5- Böjpunkterna för sannolikhetsdensitetsfunktionen ligger exakt vid μ - σ Y μ + σ.
6- Funktionen f är symmetrisk med avseende på en axel som passerar genom dess medelvärde μ y har asymptotiskt noll för x ⟶ + ∞ och x ⟶ -∞.
7- Ju högre värde på σ större spridning, buller eller avstånd från data runt medelvärdet. Det vill säga till större σ klockformen är mer öppen. Istället σ liten indikerar att tärningarna är täta mot mitten och klockans form är mer stängd eller spetsig.
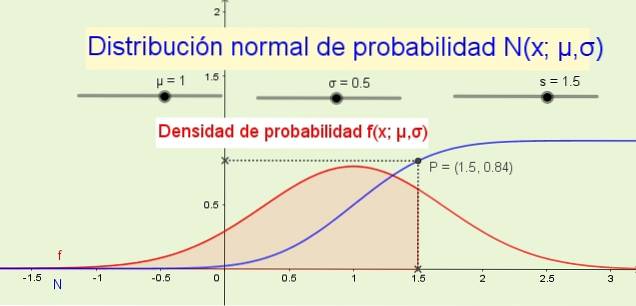
8- Distributionsfunktionen N (x; μ, σ) indikerar sannolikheten att den slumpmässiga variabeln är mindre än eller lika med x. Till exempel, i figur 1 (ovan) är sannolikheten P att variabeln x är mindre än eller lika med 1,5 är 84% och motsvarar området under sannolikhetsdensitetsfunktionen f (x; μ, σ) från -∞ till x.
Konfidensintervall
9- Om uppgifterna följer en normalfördelning är 68,26% av dessa mellan μ - σ Y μ + σ.
10- 95,44% av data som följer en normalfördelning finns mellan μ - 2σ Y μ + 2σ.
11- 99,74% av uppgifterna som följer en normalfördelning är mellan μ - 3σ Y μ + 3σ.
12- Om en slumpmässig variabel x följ en distribution N (x; μ, σ), sedan variabeln
z = (x - μ) / σ följer den normala normalfördelningen N (z, 0,1).
Ändringen av variabeln x till z Det kallas standardisering eller typning och det är mycket användbart när man använder tabellerna för standarddistributionen på data som följer en icke-standard normal distribution..
Tillämpningar av normalfördelningen
För att tillämpa normalfördelningen är det nödvändigt att gå igenom beräkningen av integralen av sannolikhetstätheten, vilket ur analytisk synvinkel inte är lätt och det finns inte alltid ett datorprogram som tillåter dess numeriska beräkning. För detta ändamål används tabellerna med normaliserade eller standardiserade värden, vilket är inget annat än normalfördelningen i fallet μ = 0 och σ = 1.
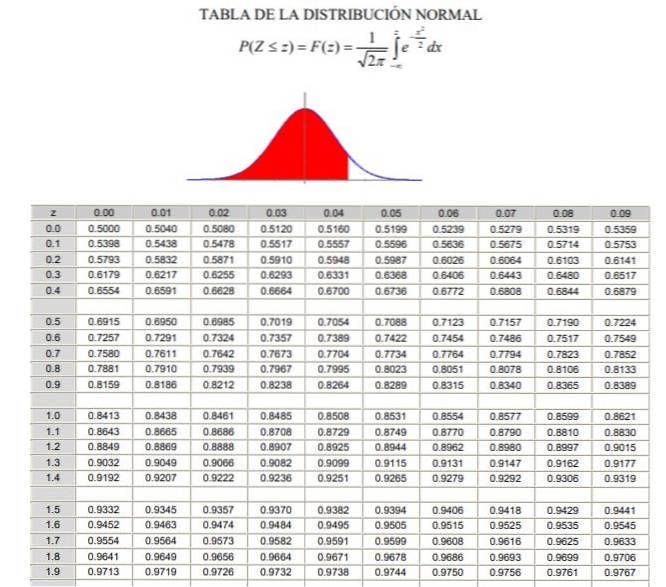
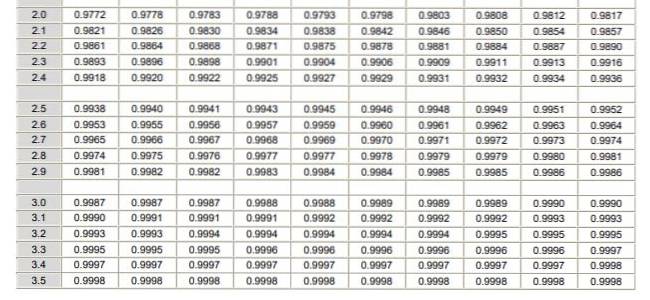
Det bör noteras att dessa tabeller inte innehåller negativa värden. Med användning av symmetriegenskaperna för den Gaussiska sannolikhetsdensitetsfunktionen kan motsvarande värden erhållas. I den lösta övningen som visas nedan anges användningen av tabellen i dessa fall.
Exempel
Anta att du har en uppsättning slumpmässiga data x som följer en normalfördelning av medelvärde 10 och standardavvikelse 2. Du ombeds att hitta sannolikheten att:
a) Den slumpmässiga variabeln x är mindre än eller lika med 8.
b) Är mindre än eller lika med 10.
c) Att variabeln x är under 12.
d) Sannolikheten att ett värde x är mellan 8 och 12.
Lösning:
a) För att svara på den första frågan måste du helt enkelt beräkna:
N (x; μ, σ)
Med x = 8, μ = 10 Y σ = 2. Vi inser att det är en integral som inte har en analytisk lösning i elementära funktioner, men lösningen uttrycks som en funktion av felfunktionen erf (x).
Å andra sidan finns det möjligheten att lösa integralen i numerisk form, vilket är vad många miniräknare, kalkylblad och datorprogram som GeoGebra gör. Följande bild visar den numeriska lösningen som motsvarar det första fallet:
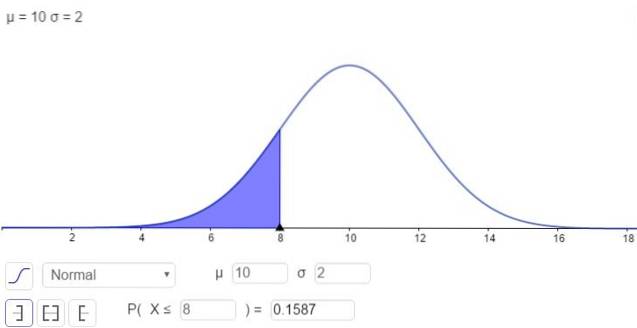
och svaret är att sannolikheten att x är under 8 är:
P (x ≤ 8) = N (x = 8; μ = 10, σ = 2) = 0,1587
b) I det här fallet försöker vi hitta sannolikheten för att den slumpmässiga variabeln x är under medelvärdet, vilket i det här fallet är värt 10. Svaret kräver ingen beräkning, eftersom vi vet att hälften av data är under genomsnittet och den andra halvan över genomsnittet. Därför är svaret:
P (x ≤ 10) = N (x = 10; μ = 10, σ = 2) = 0,5
c) För att svara på denna fråga måste du beräkna N (x = 12; μ = 10, σ = 2), Detta kan göras med en miniräknare som har statistiska funktioner eller genom programvara som GeoGebra:
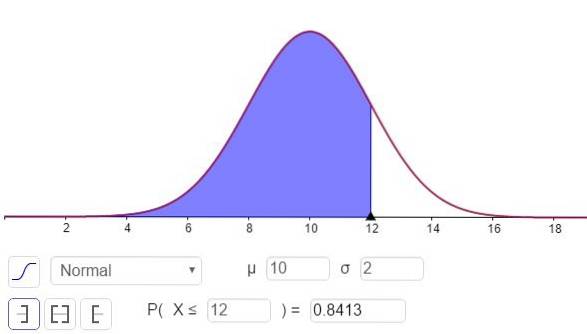
Svaret på del c kan ses i figur 3 och är:
P (x ≤ 12) = N (x = 12; μ = 10, σ = 2) = 0,8413.
d) För att hitta sannolikheten att den slumpmässiga variabeln x är mellan 8 och 12 kan vi använda resultaten av delarna a och c enligt följande:
P (8 ≤ x ≤ 12) = P (x ≤ 12) - P (x ≤ 8) = 0,8413 - 0,1587 = 0,6826 = 68,26%.
Övningen löst
Genomsnittspriset för ett företags aktie är $ 25 med en standardavvikelse på $ 4. Bestäm sannolikheten att:
a) En åtgärd kostar mindre än $ 20.
b) Det kostar mer än $ 30.
c) Priset är mellan $ 20 och $ 30.
Använd standarddistributionstabeller för att hitta svar.
Lösning:
För att kunna använda tabellerna är det nödvändigt att gå vidare till den normaliserade eller typade z-variabeln:
$ 20 i den normaliserade variabeln är lika med z = ($ 20 - $ 25) / $ 4 = -5/4 = -1,25 och
$ 30 i den normaliserade variabeln är lika med z = ($ 30 - $ 25) / $ 4 = +5/4 = +1,25.
a) $ 20 är lika med -1,25 i den normaliserade variabeln, men tabellen har inte negativa värden, så vi lägger värdet +1,25 som ger värdet 0,8944.
Om 0,5 dras från detta värde blir resultatet området mellan 0 och 1,25 som förresten är identiskt (med symmetri) till området mellan -1,25 och 0. Resultatet av subtraktionen är 0,8944 - 0,5 = 0,3944 vilket är området mellan -1,25 och 0.
Men området från -∞ till -1,25 är av intresse, vilket kommer att vara 0,5 - 0,3944 = 0,1056. Därför dras slutsatsen att sannolikheten för att ett lager är under 20 dollar är 10,56%.
b) $ 30 i den typade variabeln z är 1,25. För detta värde visas siffran 0,8944 i tabellen, vilket motsvarar området från -∞ till +1,25. Området mellan +1,25 och + ∞ är (1 - 0,8944) = 0,1056. Sannolikheten att en aktie kostar mer än $ 30 är 10,56%.
c) Sannolikheten att en åtgärd kostar mellan 20 och 30 dollar beräknas enligt följande:
100% -10,56% - 10,56% = 78,88%
Referenser
- Statistik och sannolikhet. Normal distribution. Återställd från: projectdescartes.org
- Geogebra. Klassisk geogebra, sannolikhetsberäkning. Återställd från geogebra.org
- MathWorks. Gaussisk distribution. Återställd från: es.mathworks.com
- Mendenhall, W. 1981. Statistik för management och ekonomi. 3: e. utgåva. Grupo Ledare Iberoamérica.
- Stat Trek. Lär dig själv statistik. Poisson-distribution. Återställd från: stattrek.com,
- Triola, M. 2012. Elementär statistik. 11: e. Ed Pearson Education.
- University of Vigo. Huvudsakliga kontinuerliga distributioner. Återställd från: anapg.webs.uvigo.es
- Wikipedia. Normal distribution. Återställd från: es.wikipedia.org



Ingen har kommenterat den här artikeln än.