
Translationsbalansbestämning, tillämpningar, exempel
De translationell jämvikt Det är ett tillstånd där ett objekt som helhet finns när alla krafter som verkar på det kompenseras, vilket resulterar i en noll nettokraft. Matematiskt motsvarande att säga att F1+ Ftvå + F3 +.... = 0, där F1, Ftvå, F3... de inblandade styrkorna.
Det faktum att en kropp är i translationell jämvikt betyder inte att den nödvändigtvis är i vila. Detta är ett särskilt fall av definitionen ovan. Objektet kan vara i rörelse, men i avsaknad av acceleration kommer detta att vara en enhetlig rätlinjig rörelse.

Så om kroppen är i vila fortsätter den så här. Och om den redan har rörelse kommer den att ha konstant hastighet. Generellt sett är rörelsen för något objekt en sammansättning av översättningar och rotationer. Översättningar kan vara som visas i figur 2: linjär eller krökt.
Men om en av objektets punkter är fixad, är den enda chansen att röra sig att rotera. Ett exempel på detta är en CD vars centrum är fast. CD: n har förmågan att rotera runt en axel som passerar genom den punkten, men inte att översätta.
När objekt har fasta punkter eller stöds på ytor talar vi om länkar. Länkarna samverkar och begränsar rörelserna som objektet kan göra.
Artikelindex
- 1 Bestämning av translationell jämvikt
- 1.1 Rotera ett objekt
- 1.2 Definition av vridmoment
- 1.3 Jämviktsförhållanden
- 2 applikationer
- 3 Exempel på translationell jämvikt
- 3.1 Lösning
- 4 Referenser
Bestämning av translationell jämvikt
För en partikel i jämvikt är det giltigt att säkerställa att:
FR = 0
Eller i summeringsnotation:
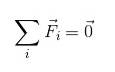
Det är tydligt att för att en kropp ska vara i translationell jämvikt måste de krafter som verkar på den kompenseras på något sätt så att deras resultat blir noll..
På detta sätt kommer objektet inte att uppleva acceleration och alla dess partiklar är i vila eller genomgår rätlinjiga översättningar med konstant hastighet..
Nu om objekt kan rotera kommer de i allmänhet att göra det. Det är därför de flesta rörelserna består av kombinationer av översättning och rotation..
Rotera ett objekt
När rotationsbalans är viktig kan det vara nödvändigt att se till att objektet inte roterar. Då är det nödvändigt att studera om det finns vridmoment eller moment som verkar på det.
Vridmoment är vektorn som rotationerna beror på. Det kräver att en kraft appliceras, men kraftens tillämpningspunkt är också viktig. För att klargöra idén, överväga ett utökat objekt som en kraft verkar på F och låt oss se om den kan producera en rotation runt någon axel O.
Det är redan intuitivt att när du trycker på objektet vid punkten P med kraften F, det är möjligt att rotera den runt punkt O, rotera moturs. Men riktningen i vilken kraften appliceras är också viktig. Till exempel kommer inte kraften som appliceras på figuren i mitten att få objektet att rotera, även om det verkligen kan flytta det..
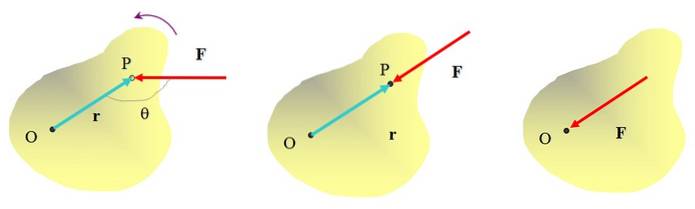
Att använda kraft direkt på punkt O vänder inte heller på objektet. Så det är tydligt att för att uppnå en rotationseffekt måste kraften appliceras på ett visst avstånd från rotationsaxeln och dess handlingslinje får inte passera genom axeln..
Definition av vridmoment
Vridmomentet eller momentet för en kraft, betecknad som τ, vektorstorleken som är ansvarig för att sammanställa alla dessa fakta, definieras som:
τ = r x F
Vektoren r den riktas från rotationsaxeln till kraftens appliceringspunkt och vinkeln mellan r och F är viktigt. Därför uttrycks vridmomentets storlek som:
τ = r.F.sen Vad
Det mest effektiva vridmomentet uppstår när r Y F de är vinkelräta.
Om det nu är önskvärt att inga rotationer sker eller dessa sker med konstant vinkelacceleration, är det nödvändigt att summan av vridmomenten som verkar på objektet är noll, analogt med vad som ansågs för krafterna:
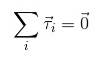
Jämviktsförhållanden
Balans betyder stabilitet, harmoni och balans. För att ett objekt ska kunna förflyttas till dessa egenskaper måste de villkor som beskrivs i föregående avsnitt tillämpas:
1) F1+ Ftvå + F3 +.... = 0
2) τ1+ τtvå + τ3 +.... = 0
Det första villkoret garanterar translationell jämvikt och det andra rotationsjämvikten. Båda måste vara uppfyllda om objektet ska stanna kvar statisk jämvikt (frånvaro av rörelse av något slag).
Applikationer
Jämviktsförhållanden är tillämpliga på många strukturer, eftersom när byggnader eller olika föremål byggs görs det med avsikt att deras delar förblir i samma relativa positioner med varandra. Med andra ord att objektet inte tas isär.
Detta är viktigt till exempel när man bygger broar som förblir fasta under foten, eller när man utformar bebodda strukturer som inte ändrar position eller har en tendens att välta..
Även om man tror att enhetlig rätlinjig rörelse är en extrem förenklad rörelse, som sällan förekommer i naturen, måste man komma ihåg att ljusets hastighet i vakuum är konstant, och ljudets ljud även om man betraktar mediet som homogent.
I många konstgjorda mobila strukturer är det viktigt att en konstant hastighet bibehålls: till exempel på rulltrappor och monteringslinjer.
Exempel på translationell jämvikt
Detta är den klassiska övningen av spänningarna som håller lampan i balans. Det är känt att lampan väger 15 kg. Hitta storleken på de spänningar som är nödvändiga för att hålla den i denna position.
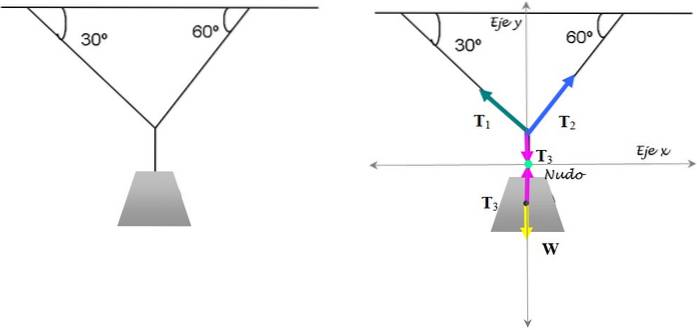
Lösning
För att lösa det fokuserar vi på knuten där de tre strängarna möts. De respektive fria kroppsdiagrammen för noden och lampan visas i figuren ovan..
Lampans vikt är W = 5 kg. 9,8 m / stvå = 49 N.. För att lampan ska vara i jämvikt är det tillräckligt att det första jämviktsvillkoret är uppfyllt:
T3 - W = 0
T3 = W = 49 N..
Spänningar T1 Y Ttvå måste sönderdelas:
T1 år + T2 och - T3 = 0 (Summan av krafter längs y-axeln)
-T1x +T2x = 0 (Summan av krafter längs x-axeln)
Tillämpa trigonometri:
T1.cos 60º + Ttvå .cos 30º = 49
- T1.sen60º + Ttvå.sin30º = 0
Det är ett system med två ekvationer med två okända, vars svar är: T1 = 24,5 N Y Ttvå = 42,4 N.
Referenser
- Rex, A. 2011. Grundläggande fysik. Pearson. 76 - 90.
- Serway, R., Jewett, J. (2008). Fysik för naturvetenskap och teknik. Volym 1. 7mamma. Ed. Cengage Learning. 120 - 124.
- Serway, R., Vulle, C. 2011. Fundamentals of Physics. 9na Ed. Cengage Learning. 99-112.
- Tippens, P. 2011. Fysik: begrepp och tillämpningar. 7: e upplagan. MacGraw Hill. 71 - 87.
- Walker, J. 2010. Fysik. Addison Wesley. 332 -346.


Ingen har kommenterat den här artikeln än.