
Provtagningsfelformler och ekvationer, beräkning, exempel
De provtagningsfel eller provfel I statistiken är det skillnaden mellan medelvärdet för ett urval och medelvärdet för den totala befolkningen. För att illustrera idén, låt oss föreställa oss att den totala befolkningen i en stad är en miljon människor, varav den genomsnittliga skostorleken önskas, för vilken ett slumpmässigt urval på tusen personer tas.
Den genomsnittliga storleken som framgår av urvalet kommer inte nödvändigtvis att sammanfalla med den för den totala befolkningen, men om provet inte är partiskt måste värdet vara nära. Denna skillnad mellan medelvärdet för urvalet och den totala populationen är provtagningsfelet.
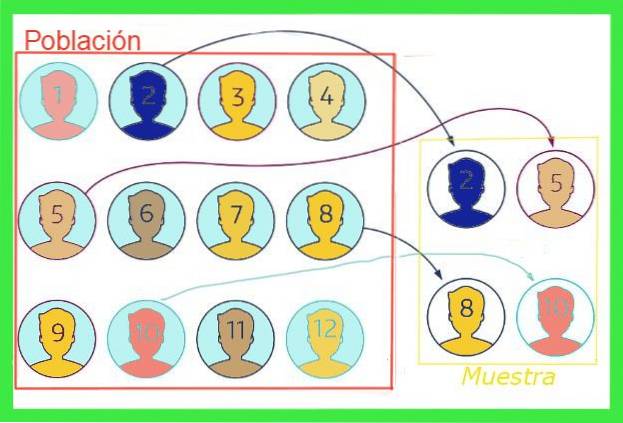
I allmänhet är medelvärdet för den totala befolkningen okänd, men det finns tekniker för att minska detta fel och formler för att uppskatta samplingsfelmarginal som kommer att exponeras i den här artikeln.
Artikelindex
- 1 Formler och ekvationer
- 2 Hur man beräknar provtagningsfel
- 2.1 För en konfidensnivå γ
- 3 Exempel
- 3.1 - Exempel 1
- 3.2 - Exempel 2
- 3.3 - Exempel 3
- 3.4 - Exempel 4
- 3.5 - Övning 5
- 4 Referenser
Formler och ekvationer
Låt oss säga att du vill veta medelvärdet för en viss mätbar egenskap x i en befolkning av storlek N, men hur N är ett stort antal, är det inte möjligt att genomföra studien på den totala befolkningen, sedan fortsätter vi med att ta en aleatory sample av storlek n<
Medelvärdet för provet betecknas med
Antag att de tar m prover från den totala befolkningen N, alla i samma storlek n med medelvärden
Dessa medelvärden kommer inte att vara identiska med varandra och kommer alla att ligga runt befolkningens medelvärde μ. De provmarginalfel E anger den förväntade separationen av medelvärdena
De standard felmarginal ε storleksprov n det är:
ε = σ / √n
var σ är standardavvikelsen (kvadratroten av variansen), som beräknas med hjälp av följande formel:
σ = √ [(x -
Meningen med standard felmarginal ε är följande:
De medelvärde
Hur man beräknar provtagningsfel
I föregående avsnitt gavs formeln för att hitta felintervall standard- av ett urval av storlek n, där ordet standard indikerar att det är en felmarginal med 68% konfidens.
Detta indikerar att om många prover av samma storlek togs n, 68% av dem ger medelvärden
Det finns en enkel regel, kallad regel 68-95-99.7 vilket gör att vi kan hitta marginalen för provtagningsfel E för konfidensnivåer av 68%, 95% Y 99,7% lätt, eftersom denna marginal är 1⋅ε, 2⋅ε och 3⋅ε respektive.
För en självförtroende γ
Om han konfidensnivå γ inte är något av ovanstående, då är samplingsfelet standardavvikelsen σ multiplicerat med faktorn Zy, som erhålls genom följande förfarande:
1.- Först signifikansnivå α som beräknas från konfidensnivå γ använder följande förhållande: a = 1 - y
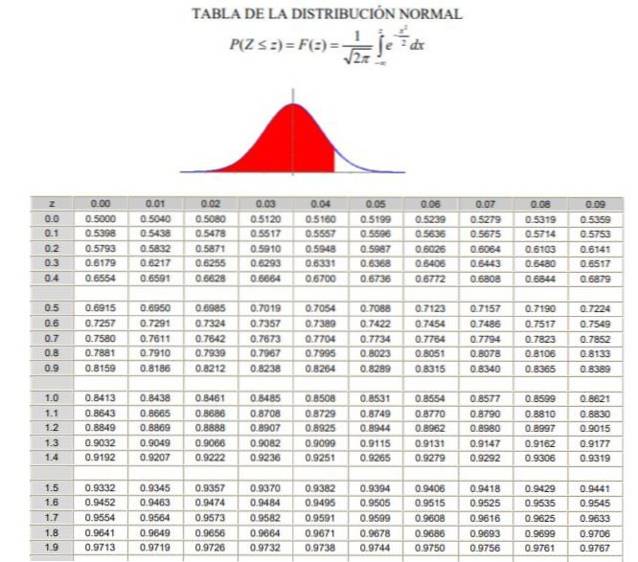
2.- Då måste du beräkna värdet 1 - a / 2 = (1 + y) / 2, vilket motsvarar den ackumulerade normala frekvensen mellan -∞ och Zy, i en normal eller standardiserad Gaussisk fördelning F (z), vars definition kan ses i figur 2.
3.- Ekvationen är löst F (Zy) = 1 - a / 2 med hjälp av tabellerna för normalfördelningen (kumulativ) F, eller med hjälp av ett datorprogram som har den inversa standardiserade Gaussiska funktionen F-1.
I det senare fallet har vi:
Z = G-1(1 - a / 2).
4. - Slutligen tillämpas denna formel för provtagningsfelet med en tillförlitlighetsnivå γ:
E = Zy⋅(σ / √n)
Exempel
- Exempel 1
Beräkna standard felmarginal i medelvikt för ett prov på 100 nyfödda. Beräkningen av genomsnittsvikten var
Lösning
De standard felmarginal det är ε = σ / √n = (1 500 kg) / √100 = 0,15 kg. Vilket innebär att man med dessa data kan dra slutsatsen att vikten på 68% av nyfödda är mellan 2950 kg och 3,25 kg.
- Exempel 2
Bestämma marginalen för provtagningsfel E och viktintervallet på 100 nyfödda med en konfidensnivå på 95% om medelvikten är 3100 kg med standardavvikelse σ = 1500 kg.
Lösning
Om regel 68; 95; 99,7 → 1⋅ε; 2⋅ε; 3⋅ε, du har:
E = 2⋅ε = 2⋅0,15 kg = 0,30 kg
Det vill säga att 95% av nyfödda har vikter mellan 2800 kg och 3400 kg.
- Exempel 3
Bestäm viktsområdet för de nyfödda från exempel 1 med en konfidensmarginal på 99,7%.
Lösning
Provtagningsfelet med 99,7% konfidens är 3 σ / √n, vilket för vårt exempel är E = 3 * 0,15 kg = 0,45 kg. Härifrån slutsatsen att 99,7% av nyfödda kommer att ha vikter mellan 2650 kg och 3550 kg.
- Exempel 4
Bestäm faktorn Zy för en tillförlitlighetsnivå på 75%. Bestäm marginalen för provtagningsfel med denna tillförlitlighetsnivå för det fall som presenteras i exempel 1.
Lösning
De självförtroendenivå det är γ = 75% = 0,75 som är relaterat till signifikansnivå a genom förhållande γ= (1 - a), så att signifikansnivån är a = 1 - 0,75 = 0,25.
Detta innebär att den kumulativa normala sannolikheten mellan -∞ och Zy det är:
P (Z ≤ Zy ) = 1 - 0,125 = 0,875
Vad motsvarar ett värde Zy 1.1503, som visas i figur 3.
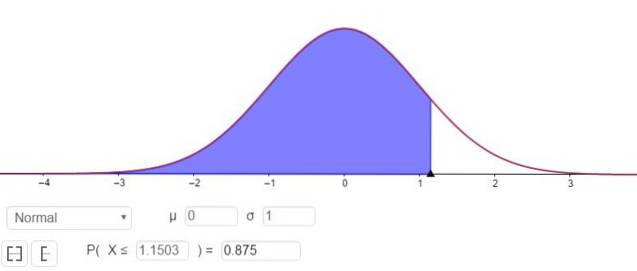
Det vill säga provtagningsfelet är E = Zy⋅(σ / √n)= 1.15⋅(σ / √n).
När det tillämpas på data från exempel 1 ger det ett fel på:
E = 1,15 * 0,15 kg = 0,17 kg
Med en konfidensnivå på 75%.
- Övning 5
Vad är konfidensnivån om Za / 2 = 2,4 ?
Lösning
P (Z
P (Z ≤ 2,4) = 1 - α / 2 = 0,9918 → α / 2 = 1 - 0,9918 = 0,0082 → α = 0,0164
Betydelsesnivån är:
a = 0,0164 = 1,64%
Och slutligen kvarstår konfidensnivån:
1- a = 1 - 0,0164 = 100% - 1,64% = 98,36%
Referenser
- Canavos, G. 1988. Sannolikhet och statistik: Tillämpningar och metoder. Mcgraw hill.
- Devore, J. 2012. Sannolikhet och statistik för teknik och vetenskap. 8: e. Utgåva. Cengage.
- Levin, R. 1988. Statistik för administratörer. 2: a. Utgåva. Prentice hall.
- Sudman, S. 1982. Ställa frågor: En praktisk guide till utformning av frågeformulär. San Francisco. Jossey bas.
- Walpole, R. 2007. Sannolikhet och statistik för teknik och vetenskap. Pearson.
- Wonnacott, T.H. och R.J. Wonnacott. 1990. Inledande statistik. 5: e utgåvan Wiley
- Wikipedia. Provtagningsfel. Återställd från: en.wikipedia.com
- Wikipedia. Felmarginal. Återställd från: en.wikipedia.com



Ingen har kommenterat den här artikeln än.