
Inferentiell statistikhistoria, egenskaper, vad den är till för, exempel

De inferentiell statistik eller deduktiv statistik är en som härleder egenskaperna hos en population från prover som tagits från den, genom en serie analystekniker. Med den erhållna informationen utvecklas modeller som sedan möjliggör förutsägelser om beteendet hos nämnda befolkning..
Av denna anledning har slutlig statistik blivit den främsta vetenskapen när det gäller att erbjuda det stöd och de instrument som otaliga discipliner kräver när man fattar beslut..

Fysik, kemi, biologi, teknik och samhällsvetenskap har ständigt nytta av dessa verktyg när de skapar sina modeller och utformar och implementerar experiment..
Artikelindex
- 1 Kort historik av slutsatsstatistik
- 1.1 Romerska riket
- 1.2 Medeltiden
- 1.3 Modern tid
- 1.4 Samtida ålder
- 2 funktioner
- 3 Vad är beskrivande statistik för? Applikationer
- 3.1 Sociologi och demografiska studier
- 3.2 Teknik
- 3.3 Ekonomi och företagsekonomi
- 4 Exempel på slutsatsstatistik
- 4.1 Exempel 1
- 4.2 Exempel 2
- 5 grundläggande begrepp i inferentiell statistik
- 5.1 Händelse
- 5.2 Provutrymme
- 5.3 Befolkning och prov
- 5.4 Provtagning
- 5.5 Statistiska variabler
- 5.6 Sannolikhetsfördelningar
- 5.7 Parametrar och statistik
- 5.8 Statistisk hypotes
- 5.9 Hypotesprov
- 6 Intressanta ämnen
- 7 Referenser
Kort historia av inferentiell statistik
Statistik uppstod under antiken på grund av att människor behövde organisera saker och optimera resurser. Före uppfinningen av skrift fördes register över antal personer och tillgängligt boskap med symboler som var graverade i sten..
Senare lämnade de kinesiska, babyloniska och egyptiska härskarna uppgifter om mängden grödor och antalet invånare, graverade på lertavlor, kolumner och monument..
Romerska imperiet
När Rom utövade sitt herravälde i Medelhavet var det vanligt att myndigheterna genomför folkräkningar vart femte år. Faktum är att ordet "statistik" kommer från det italienska ordet statista, vad betyder det att uttrycka.
Samtidigt höll också de stora pre-colombianska imperierna liknande register i Amerika.
Medeltiden
Under medeltiden registrerade Europas regeringar, liksom kyrkan, ägande av mark. Sedan gjorde de samma sak med födslar, dop, äktenskap och dödsfall.
Modern tid
Den engelska statistikern John Graunt (1620-1674) var den första som förutspådde baserat på sådana listor, till exempel hur många människor som kan dö av vissa sjukdomar och den uppskattade andelen manliga och kvinnliga födelser. Av denna anledning anses han vara fader till demografi..
Samtida ålder
Senare, med tillkomsten av sannolikhetsteorin, upphörde statistiken att vara enbart en samling organisationstekniker och uppnådde ett oväntat omfång som en förutsägbar vetenskap..
Således kunde experterna börja utveckla modeller för befolkningernas beteende och med dem härleda vilka saker som kunde hända med människor, föremål och till och med idéer.
Egenskaper

Nedan har vi de mest relevanta egenskaperna hos denna gren av statistik:
- Inferentiell statistik studerar en befolkning som tar ett representativt urval från den.
- Valet av provet utförs genom olika förfaranden, de mest lämpliga är de som väljer komponenterna slumpmässigt. Således har alla delar av befolkningen samma sannolikhet att väljas och därmed undviks oönskade fördomar..
- För att organisera den insamlade informationen används beskrivande statistik.
- Statistiska variabler beräknas på urvalet som används för att uppskatta befolkningens egenskaper..
- Inferentiell eller deduktiv statistik använder sannolikhetsteorin för att studera slumpmässiga händelser, det vill säga de som uppstår tillfälligt. Varje händelse tilldelas en viss sannolikhet för händelse.
- Den konstruerar hypoteser - antaganden - om befolkningens parametrar och kontrasterar dem, för att ta reda på om de är korrekta eller inte, och beräknar också konfidensnivån för svaret, det vill säga det ger en felmarginal. Den första proceduren kallas hypotes testning, medan felmarginalen är konfidensintervall.
Vad är beskrivande statistik för? Applikationer

Att studera en befolkning i sin helhet kan kräva mycket resurser i pengar, tid och ansträngning. Det är att föredra att ta representativa prover som är mycket mer hanterbara, samla in data från dem och skapa hypoteser eller antaganden om provbeteende.
När hypoteserna har fastställts och deras giltighet har testats utvidgas resultaten till befolkningen och används för att fatta beslut..
De hjälper också till att skapa modeller för den befolkningen, för att göra prognoser för framtiden. Därför är inferentiell statistik en mycket användbar vetenskap för:
Sociologi och demografiska studier
Dessa är perfekta användningsområden, eftersom statistiska tekniker tillämpas med tanken att skapa olika modeller för mänskligt beteende. Något som a priori är ganska komplicerat, eftersom många variabler ingriper.
I politiken används det vid valstid för att känna väljarnas rösträtt, på detta sätt utformar partierna strategier.
teknik
Inferensiell statistikmetoder används ofta inom teknik, de viktigaste applikationerna är kvalitetskontroll och processoptimering, till exempel förbättrar tiderna när du utför uppgifter, samt förhindrar arbetsolyckor..
Ekonomi och företagsekonomi
Med deduktiva metoder kan du utföra prognoser om driften av ett företag, den förväntade försäljningsnivån samt hjälp när du fattar beslut.
Till exempel kan deras tekniker användas för att uppskatta vilken reaktion köparna har på en ny produkt som snart kommer att lanseras på marknaden..
Det tjänar också till att utvärdera hur förändringar i människors konsumtionsvanor är, med tanke på viktiga händelser, såsom COVID-epidemin..
Exempel på slutsatsstatistik
Exempel 1
Ett enkelt deduktivt statistikproblem är följande: en matematiklärare ansvarar för fem delar av elementär algebra på ett universitet och bestämmer sig för att använda medelbetygen på bara en av dess avsnitt för att uppskatta genomsnittet av Allt.

En annan möjlighet är att ta ett urval från varje avsnitt, studera dess egenskaper och utvidga resultaten till alla avsnitt..
Exempel 2
Chefen för en damklädaffär vill veta hur mycket en viss blus kommer att sälja under sommarsäsongen. För att göra detta analyserar den försäljningen av plagget under säsongens två första veckor och bestämmer därmed trenden..
Grundläggande begrepp i inferentiell statistik
Det finns flera nyckelbegrepp, inklusive de som kommer från sannolikhetsteori, som du måste vara tydlig för att förstå hela teknikens omfattning. Vissa, som en population och ett urval, har vi redan nämnt i hela texten.
Händelse
En händelse eller händelse är något som händer, och som kan ha flera resultat. Ett exempel på en händelse kan vara att vända ett mynt och det finns två möjliga resultat: huvuden eller svansar.
Provutrymmet
Det är en uppsättning av alla möjliga resultat av en händelse.
Befolkning och prov
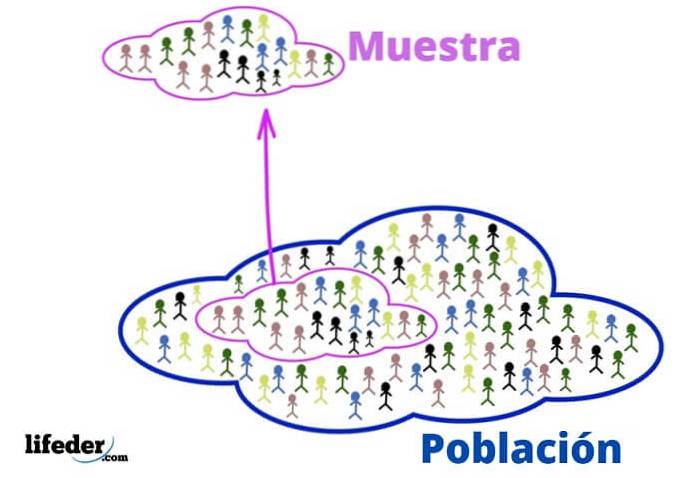
Befolkningen är det universum som du vill studera. Det handlar inte nödvändigtvis om människor eller levande varelser, eftersom befolkningen i statistik kan bestå av objekt eller idéer.
För sin del är urvalet en delmängd av populationen, extraheras noggrant ur den eftersom den är representativ..
Provtagning
Det är den uppsättning tekniker som ett urval väljs från en viss population. Provtagning kan vara slumpmässig om probabilistiska metoder används för att välja provet, eller icke-probabilistiska, om analytikern har sina egna urvalskriterier, enligt hans erfarenhet..
Statistiska variabler
Uppsättning av värden som kan ha egenskaperna hos befolkningen. De klassificeras på olika sätt, till exempel kan de vara diskreta eller kontinuerliga. Med hänsyn till deras natur kan de också vara kvalitativa eller kvantitativa..
Sannolikhetsfördelningar
Sannolikhetsfunktioner som beskriver beteendet hos ett stort antal system och situationer som observerats i naturen. De mest kända är den Gaussiska eller Gaussiska klockfördelningen och binomialfördelningen.
Parametrar och statistik
Uppskattningsteorin fastställer att det finns ett samband mellan värdena för befolkningen och värdena för urvalet från den populationen. De parametrar är de egenskaper hos befolkningen som vi inte känner till men vill uppskatta: till exempel medelvärdet och standardavvikelsen.
För deras del statistik är provets egenskaper, till exempel dess medelvärde och standardavvikelse.
Antag som ett exempel att befolkningen består av alla ungdomar mellan 17 och 30 år i ett samhälle, och vi vill veta andelen personer som för närvarande har högre utbildning. Detta skulle vara populationsparametern att bestämma.
För att uppskatta det väljs ett slumpmässigt urval på 50 ungdomar och andelen av dem som studerar vid universitet eller högskolor beräknas. Denna andel är statistiken.
Om det efter studien fastställs att 63% av de 50 ungdomarna går i högre utbildning är detta befolkningsberäkningen, gjord av urvalet.
Detta är bara ett exempel på vad inferentiell statistik kan göra. Det är känt som uppskattning, men det finns också tekniker för att förutsäga statistiska variabler, liksom för att fatta beslut.
Statistisk hypotes
Det är en gissning som görs beträffande värdet av medelvärdet och standardavvikelsen för någon egenskap hos befolkningen. Om inte befolkningen är fullständigt undersökt är dessa okända värden.
Hypotes testning
Är antagandena om befolkningsparametrarna giltiga? För att få reda på verifieras det om resultaten från provet stöder dem eller inte, så det är nödvändigt att utforma hypotesprov.
Det här är de allmänna stegen för att utföra ett:
Steg 1
Identifiera vilken typ av distribution befolkningen förväntas följa.
Steg 2
Ange två hypoteser, betecknade som Heller och H1. Den första är nollhypotesen där vi antar att parametern har ett visst värde. Den andra är den alternativa hypotesen vilket antar ett annat värde än nollhypotesen. Om detta avvisas accepteras den alternativa hypotesen.
Steg 3
Upprätta en acceptabel marginal för skillnaden mellan parametern och statistiken. Dessa kommer sällan att visa sig vara identiska, även om de förväntas vara mycket nära..
Steg 4
Föreslå ett kriterium för att acceptera eller avvisa nollhypotesen. För detta används en teststatistik, vilket kan vara medelvärdet. Om medelvärdet ligger inom vissa gränser accepteras nollhypotesen, annars avvisas den.
Steg 5
Som ett sista steg bestäms om nollhypotesen ska accepteras eller inte..
Teman av intresse
Grenar av statistik.
Statistiska variabler.
Befolkning och prov.
Beskrivande statistik.
Referenser
- Berenson, M. 1985. Statistik för management och ekonomi, begrepp och tillämpningar. Redaktionellt Interamericana.
- Canavos, G. 1988. Sannolikhet och statistik: Tillämpningar och metoder. Mcgraw hill.
- Devore, J. 2012. Sannolikhet och statistik för teknik och vetenskap. 8: e. Utgåva. Cengage Learning.
- Statistikhistoria. Återställd från: eumed.net.
- Ibañez, s. 2010. Matematik II. Kompetensmetod. Cengage Learning.
- Levin, R. 1981. Statistik för administratörer. Prentice hall.
- Walpole, R. 2007. Sannolikhet och statistik för teknik och vetenskap. Pearson.



Ingen har kommenterat den här artikeln än.