De grad av ett polynom på a variabel ges av termen som har den största exponenten, och om polynom har två eller flera variabler, sedan bestäms graden av summan av exponenterna för varje term, den större summan är graden av polynomet.
Låt oss se hur man bestämmer graden av polynom på ett praktiskt sätt.
Antag att polynomet P (x) = -5x + 8x3 + 7 - 4xtvå. Denna polynom är en variabel, i detta fall är den variabeln x. Detta polynom består av flera termer, som är följande:
-5x; 8x3; 7; - 4xtvå
Låt oss välja bland de fyra termerna vars exponent är större, den här termen är:
8x3
Och vad är nu exponenten? Svaret är 3. Därför är P (x) ett polynom av grad 3.
Om polynomet i fråga har mer än en variabel kan graden vara:
-Absolut
-I förhållande till en variabel
Den absoluta graden finns som förklarats i början: lägga till exponenterna för varje term och välja den största.
Å andra sidan är graden av polynom med avseende på en av variablerna eller bokstäverna det största värdet på exponenten som nämnda bokstav har. Poängen kommer att bli tydligare med exemplen och de lösta övningarna i följande avsnitt.
Artikelindex
Polynom kan klassificeras efter grad och kan vara första grad, andra grad, tredje grad och så vidare. För exemplet i figur 1 är energin ett monomium av första graden för massan.
Det är också viktigt att notera att antalet termer som ett polynom har är lika med betyg plus 1. A) Ja:
-Första grads polynom har två termer: a1x + aeller
-Andra gradens polynom har tre termer: atvåxtvå + till1x + aeller
-En tredje graders polynom har fyra termer: a3x3 + tilltvåxtvå + till1x + aeller
Och så vidare. Den noggranna läsaren har märkt att polynomierna i de föregående exemplen är skrivna i form minskar, det vill säga att placera termen först med Högsta graden.
Följande tabell visar olika polynom, både av en och flera variabler och deras respektive absoluta grader:
| Polynom | Kvalitet |
|---|---|
| 3x4+5x3-2x + 3 | 4 |
| 7x3-2xtvå+3x-6 | 3 |
| 6 | 0 |
| x-1 | 1 |
| x5-bx4+abx3+ab3xtvå | 6 |
| 3x3Y5 + 5xtvåY4 - 7xytvå + 6 | 8 |
De två sista polynomerna har mer än en variabel. Av dessa har termen med den högsta absoluta graden markerats med fet stil, så att läsaren snabbt kan kontrollera graden. Det är viktigt att komma ihåg att när variabeln inte har en skriftlig exponent, är det underförstått att nämnda exponent är lika med 1.
Till exempel i den angivna termen ab3xtvå det finns tre variabler, nämligen: till, b Y x. Under den termen, till höjs till 1, det vill säga:
a = a1
Därför ab3xtvå = a1b3xtvå
Eftersom exponenten för b är 3 och den för x är 2, följer det omedelbart att graden av denna term är:
1 + 3 + 2 = 6
Y är den absoluta graden av polynom, eftersom ingen annan term har en högre grad.
När du arbetar med polynom är det viktigt att vara uppmärksam på graden av det, eftersom det först och innan du utför någon operation är det praktiskt att följa dessa steg, där graden ger mycket viktig information:
-Beställ polynom av preferens i minskande riktning. På detta sätt är termen med den högsta graden till vänster och termen med den lägsta graden till höger..
-Minska liknande termer, ett förfarande som består i att lägga algebraiskt till alla termer för samma variabel och grad som finns i uttrycket.
-Om det behövs fylls polynomierna in och infogar termer vars koefficient är 0, om det saknas termer med någon exponent.
Med tanke på polynomet P (x) = 6xtvå - 5x4- 2x + 3x + 7 + 2x5 - 3x3 + x7 -12 ombeds det att beställa det i fallande ordning, minska de liknande termerna om det finns och komplettera de saknade villkoren om det behövs.
Det första man ska leta efter är termen med den största exponenten, vilket är graden av polynom, som visar sig vara:
x7
Därför är P (x) av grad 7. Därefter ordnas polynomet som börjar med denna term till vänster:
P (x) = x7 + 2x5 - 5x4 - 3x3 + 6xtvå - 2x + 3x + 7-12
Nu reduceras liknande villkor, vilket är följande: - 2x och 3x å ena sidan. Och 7 och -12 å andra sidan. För att minska dem läggs koefficienterna algebraiskt och variabeln lämnas oförändrad (om variabeln inte visas bredvid koefficienten, kom ihåg att x0 = 1):
-2x + 3x = x
7-12 = -5
Ersätt dessa resultat i P (x):
P (x) = x7 +2x5 - 5x4 - 3x3 + 6xtvå + x -5
Och slutligen undersöks polynomet för att se om någon exponent saknas och faktiskt en term vars exponent är 6 saknas, därför kompletteras den med nollor så här:
P (x) = x7 + 0x6 +2x5 - 5x4 - 3x3 + 6xtvå + x - 5
Nu observeras att polynomet lämnades med 8 termer, eftersom som sagt tidigare är antalet termer lika med grad + 1.
Med polynom kan du utföra additions- och subtraktionsoperationer, där endast samma termer läggs till eller subtraheras, vilka är de med samma variabel och samma grad. Om det inte finns några liknande termer, anges tillägget eller subtraktionen helt enkelt.
När tillägget eller subtraktionen har genomförts, varvid den senare är summan av det motsatta, är graden av det resulterande polynomet alltid lika med eller mindre än graden av polynom som adderar den högsta graden.
Hitta följande summa och bestäm den absoluta graden:
till3- 8axtvå + x3 + 5: etvåx - 6axtvå - x3 + 3: e3 - 5: etvåx - x3 + till3+ 14axtvå - x3
Det är ett polynom med två variabler, så det är bekvämt att reducera liknande termer:
till3- 8axtvå + x3 + 5: etvåx - 6axtvå - x3 + 3: e3 - 5: etvåx - x3 + till3+ 14axtvå - x3 =
= a3 + 3: e3 + till3 - 8axtvå - 6axtvå+ 14axtvå +5: etvåx - 5: etvåx + x3- x3- x3- x3 =
= 5a3 - 2x3
Båda termerna är av grad 3 i varje variabel. Därför är den absoluta graden av polynom 3.
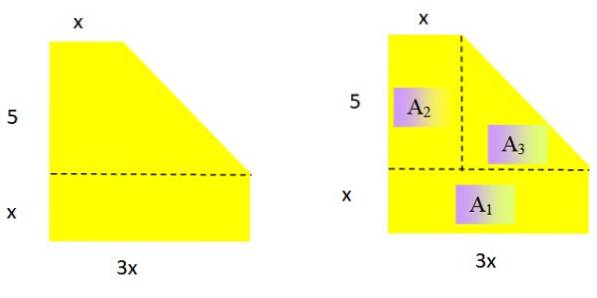
Uttryck ytan för följande plan geometriska figur som ett polynom (figur 2 till vänster). Vad är graden av det resulterande polynomet?
Eftersom det är ett område måste det resulterande polynomet vara av grad 2 i variabeln x. För att bestämma ett lämpligt uttryck för området sönderdelas figuren i kända områden:
Området för en rektangel respektive en triangel är: bas x höjd Y bas x höjd / 2
TILL1 = x. 3x = 3xtvå; TILLtvå = 5. x = 5x; TILL3 = 5. (2x / 2) = 5x
Notera: basen av triangeln är 3x - x = 2x och dess höjd är 5.
Nu läggs de tre erhållna uttrycken till, med detta har vi arean av figuren som en funktion av x:
3xtvå + 5x + 5x = 3xtvå + 10x
Ingen har kommenterat den här artikeln än.