
Vector Algebra Fundamentals, Magnitudes, Vectors
De vektoralgebra är en gren av matematik som ansvarar för att studera system av linjära ekvationer, vektorer, matriser, vektorrymden och deras linjära transformationer. Det är relaterat till områden som teknik, upplösning av differentialekvationer, funktionell analys, operationsforskning, datorgrafik, bland andra..
Ett annat område som linjär algebra har antagit är fysik, eftersom det genom detta har varit möjligt att utveckla studiet av fysiska fenomen och beskriva dem genom användning av vektorer. Detta har möjliggjort en bättre förståelse av universum.

Artikelindex
- 1 Grundläggande
- 1.1 Geometriskt
- 1.2 Analytiskt
- 1.3 Axiomatiskt
- 2 magnituder
- 2.1 Skalarstorlek
- 2.2 Vektorstorlek
- 3 Vad är vektorer?
- 3.1 Modul
- 3.2 Adress
- 3.3 Känsla
- 4 Klassificering av vektorer
- 4.1 Fast vektor
- 4.2 Gratis vektor
- 4.3 Glidande vektor
- 5 Egenskaper hos vektorer
- 5.1 teamlinsvektorer
- 5.2 Motsvarande vektorer
- 5.3 Jämställdhet av vektorer
- 5.4 Motsatta vektorer
- 5.5 Enhetsvektor
- 5.6 Nollvektor
- 6 Komponenter i en vektor
- 6.1 Exempel
- 7 Operationer med vektorer
- 7.1 Addition och subtraktion av vektorer
- 7.2 Multiplikation av vektorer
- 8 Referenser
Grundläggande
Vektoralgebra härstammar från studien av kvaternioner (utvidgning av reella tal) 1, i, j och k, samt från den kartesiska geometrin som främjas av Gibbs och Heaviside, som insåg att vektorer skulle fungera som ett instrument för att representera olika fysiska fenomen.
Vektoralgebra studeras genom tre grundläggande:
Geometriskt
Vektorer representeras av linjer som har en orientering och operationer som addition, subtraktion och multiplikation med reella tal definieras genom geometriska metoder..
Analytiskt
Beskrivningen av vektorer och deras operationer görs med siffror, kallade komponenter. Denna typ av beskrivning är resultatet av en geometrisk representation eftersom ett koordinatsystem används.
Axiomatiskt
En beskrivning av vektorerna görs, oberoende av koordinatsystemet eller någon typ av geometrisk representation.
Studien av figurer i rymden görs genom deras representation i ett referenssystem, som kan ha en eller flera dimensioner. Bland de viktigaste systemen är:
- Ett-dimensionellt system, som är en linje där en punkt (O) representerar ursprunget och en annan punkt (P) bestämmer skalan (längd) och dess riktning:
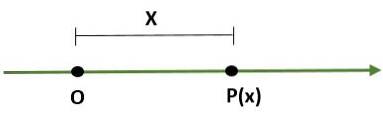
- Rektangulärt koordinatsystem (tvådimensionellt), som består av två vinkelräta linjer som kallas x-axeln och y-axeln, som passerar genom ett punkt (O) ursprung; på detta sätt är planet uppdelat i fyra regioner som kallas kvadranter. I detta fall ges en punkt (P) i planet av de avstånd som finns mellan axlarna och P.
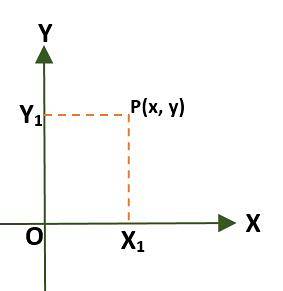
- Polarkoordinatsystem (tvådimensionellt). I detta fall består systemet av en punkt O (ursprung) som kallas polen och en stråle med ursprung i O kallas polaxeln. I detta fall ges punkten P på planet, med hänvisning till polen och polaxeln, av vinkeln (Ɵ), som bildas av avståndet mellan ursprunget och punkten P.
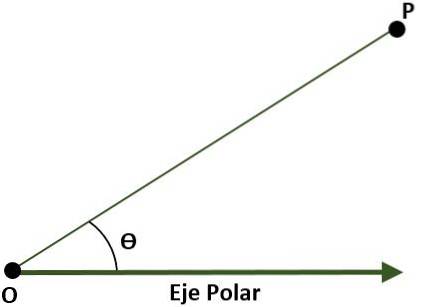
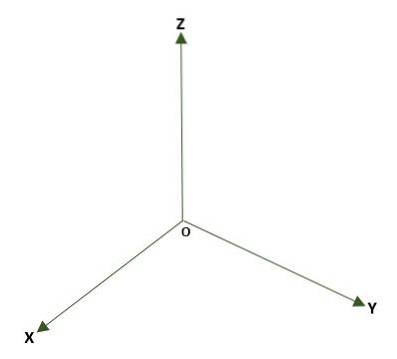
- Rektangulärt tredimensionellt system, bildat av tre vinkelräta linjer (x, y, z) vars ursprung är en punkt O i rymden. Tre koordinatplan bildas: xy, xz och yz; utrymmet kommer att delas in i åtta regioner som kallas oktanter. Referensen för en punkt P i rymden ges av avstånden som finns mellan planen och P.
Magnituder
En storlek är en fysisk storlek som kan räknas eller mätas genom ett numeriskt värde, som i fallet med vissa fysiska fenomen; emellertid är det ofta nödvändigt att kunna beskriva dessa fenomen med andra faktorer än numeriska. Det är därför storheterna klassificeras i två typer:
Skalarstorlek
De är de kvantiteter som definieras och representeras numeriskt; det vill säga genom en modul tillsammans med en måttenhet. Till exempel:
a) Tid: 5 sekunder.
b) Massa: 10 kg.
c) Volym: 40 ml.
d) Temperatur: 40 ºC.
Vector magnitude
De är de kvantiteter som definieras och representeras av en modul tillsammans med en enhet, liksom av en känsla och riktning. Till exempel:
a) Hastighet: (5ȋ - 3ĵ) m / s.
b) Acceleration: 13 m / stvå; S 45º E.
c) Kraft: 280 N, 120º.
d) Vikt: -40 ĵ kg-f.
Vektormängder representeras grafiskt av vektorer.
Vad är vektorer?
Vektorer är grafiska representationer av en vektormängd; det vill säga de är linjesegment där deras sista ände är en pilspets.
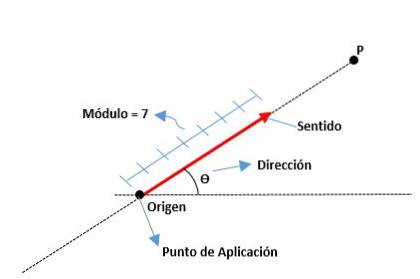
Dessa bestäms av dess modul- eller segmentlängd, dess riktning, som indikeras av pilens spets, och dess riktning enligt den linje som den tillhör. Ursprunget till en vektor är också känd som applikationspunkten.
Elementen i en vektor är som följer:
Modul
Det är avståndet från ursprunget till slutet av en vektor, representerat av ett reellt tal tillsammans med en enhet. Till exempel:
| OM | = | A | = A = 6 cm
Riktning
Det är måttet på vinkeln som finns mellan x-axeln (från det positiva) och vektorn, liksom kardinalpunkterna (norr, söder, öst och väst) används.
Känsla
Den ges av pilspetsen i slutet av vektorn och anger vart den ska.
Klassificering av vektorer
Generellt klassificeras vektorer som:
Fast vektor
Det är en vars tillämpningspunkt (ursprung) är fast; det vill säga, det förblir kopplat till en punkt i rymden, så det kan inte röra sig i detta.
Gratis vektor
Den kan röra sig fritt i rymden eftersom dess ursprung rör sig till vilken punkt som helst utan att ändra modul, riktning eller riktning..
Skjutreglervektor
Det är en som kan överföra sitt ursprung längs sin handlingslinje utan att ändra sin modul, riktning eller riktning..
Egenskaper hos vektorer
Bland de viktigaste egenskaperna hos vektorer är följande:
Vektorer teamlinser
De är de fria vektorerna som har samma modul, riktning (eller de är parallella) och avkänns som en glidande vektor eller en fast vektor.
Motsvarande vektorer
Det inträffar när två vektorer har samma riktning (eller är parallella), samma avkänning, och trots att de har olika moduler och applikationspunkter orsakar de samma effekter.
Vector jämlikhet
Dessa har samma modul, riktning och känsla, även när deras startpunkter är olika, vilket gör att en parallell vektor kan översätta sig själv utan att påverka den..
Motsatta vektorer
Det är de som har samma modul och riktning, men deras känsla är motsatt.
Enhetsvektor
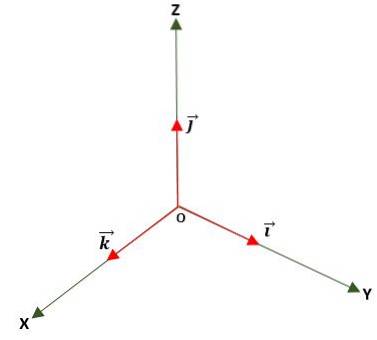
Det är en modul där modulen är lika med enheten (1). Detta erhålls genom att dela vektorn med dess modul och används för att bestämma riktningen och avkänningen för en vektor, antingen i planet eller i rymden, med bas- eller normaliserade enhetsvektorer, vilka är:
Null vektor
Det är den vars modul är lika med 0; det vill säga dess ursprung och slut sammanfaller vid samma punkt.
Komponenter i en vektor
Komponenterna i en vektor är värdena för vektorn utsprång på referenssystemets axlar; Beroende på sönderdelningen av vektorn, som kan vara på två- eller tredimensionella axlar, kommer två eller tre komponenter att erhållas..
Komponenterna i en vektor är reella tal, som kan vara positiva, negativa eller till och med noll (0).
Således, om vi har en vektor Ā, med ursprung i ett rektangulärt koordinatsystem i xy-planet (tvådimensionellt), är projektionen på x-axeln Āx och projektionen på y-axeln är Āy. Sålunda kommer vektorn att uttryckas som summan av dess komponentvektorer.
Exempel
Första exemplet
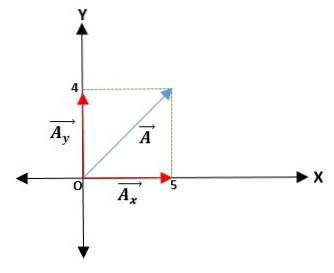
Vi har en vektor Ā som börjar från ursprunget och koordinaterna för dess ändar ges. Således är vektorn Ā = (Āx; TILLY) = (4; 5) cm.
Om vektorn Ā verkar vid ursprunget till ett tredimensionellt triangulärt koordinatsystem (i rymden) x, y, z, till en annan punkt (P), kommer projektionerna på dess axlar att vara Āx, Āy och Āz; sålunda kommer vektorn att uttryckas som summan av dess trekomponentvektorer.
Andra exemplet
Vi har en vektor Ā som börjar från ursprunget och koordinaterna för dess ändar ges. Således är vektorn Ā = (Ax; TILLY; TILLz) = (4; 6; -3) cm.
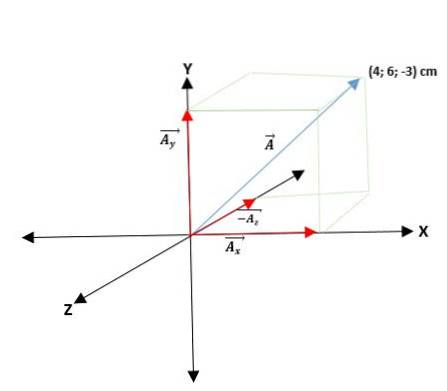
Vektorer som har sina rektangulära koordinater kan uttryckas i termer av deras basvektorer. För det behöver du bara multiplicera varje koordinat med respektive enhetsvektor, på ett sådant sätt att de för planet och utrymmet kommer att vara följande:
För planet: Ā = Axi + A.Yj.
För utrymmet: Ā = Axi + A.Yj + A.zk.
Vektoroperationer
Det finns många mängder som har en modul, avkänning och riktning, såsom acceleration, hastighet, förskjutning, kraft, bland andra..
Dessa tillämpas inom olika vetenskapsområden, och för att tillämpa dem är det i vissa fall nödvändigt att utföra operationer som addition, subtraktion, multiplikation och delning av vektorer och skalar..
addition och subtraktion av vektorer
Tillägg och subtraktion av vektorer anses vara en enda algebraisk operation eftersom subtraktionen kan skrivas som en summa; till exempel kan subtraheringen av vektorerna Ā och Ē uttryckas som:
Ā - Ē = Ā + (-Ē)
Det finns olika metoder för att utföra addition och subtraktion av vektorer: de kan vara grafiska eller analytiska.
Grafiska metoder
Används när en vektor har en modul, avkänning och riktning. För detta dras linjer som bildar en figur som senare hjälper till att avgöra resultatet. Bland de mest kända är följande:
Parallelogrammetod
För att göra tillsättningen eller subtraheringen av två vektorer väljs en gemensam punkt på koordinataxeln - som representerar vektorernas ursprungspunkt - med bibehållen modul, riktning och riktning..
Linjer ritas sedan parallellt med vektorerna för att bilda ett parallellogram. Den resulterande vektorn är diagonalen som går från båda vektorernas ursprungspunkt till parallellogramets topp:
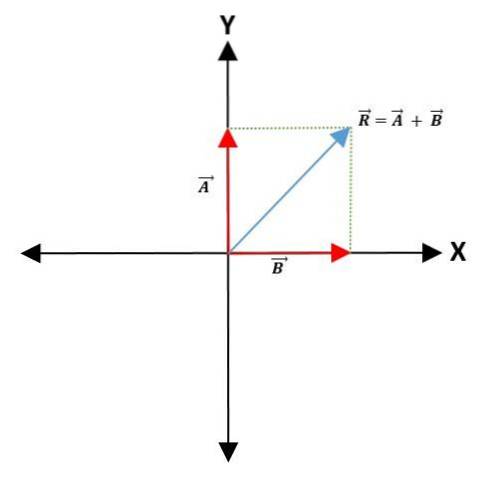
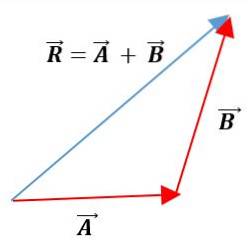
Triangelmetod
I denna metod placeras vektorerna efter varandra med behållning av sina moduler, riktningar och riktningar. Den resulterande vektorn kommer att vara föreningen av ursprunget för den första vektorn med slutet av den andra vektorn:
analytiska metoder
Två eller flera vektorer kan läggas till eller subtraheras genom en geometrisk metod eller vektormetod:
Geometrisk metod
När två vektorer bildar en triangel eller ett parallellogram kan den resulterande vektorn modul och riktning bestämmas med hjälp av sinus och cosinus. Således ges modulen för den resulterande vektorn, som tillämpar cosinuslagen och med triangelmetoden, av:
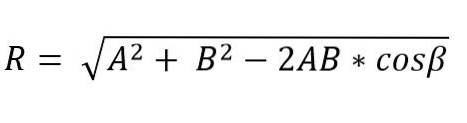
I denna formel är β vinkeln motsatt sidan R, och detta är lika med 180º - Ɵ.
I stället är metoden för den resulterande vektorn enligt parallellogrammetoden:
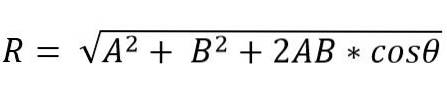
Riktningen för den resulterande vektorn ges av vinkeln (a), som bildar den resulterande med en av vektorerna.
Enligt sinuslagen kan addition eller subtraktion av vektorer också göras med triangeln eller parallellogrammetoden, med vetskap om att i varje triangel är sidorna proportionella mot vinklarnas sines:
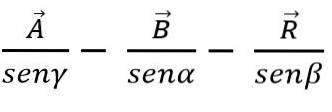
Vektor metod
Detta kan göras på två sätt: beroende på dess rektangulära koordinater eller dess basvektorer.
Det kan göras genom att översätta vektorerna som ska läggas till eller subtraheras mot koordinaternas ursprung, och sedan alla projektionerna på var och en av axlarna för planet (x, y) eller mellanslag (x och Z); slutligen läggs dess komponenter algebraiskt till. Så för planet är det:
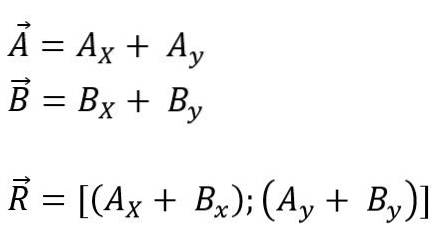
Modulen för den resulterande vektorn är:
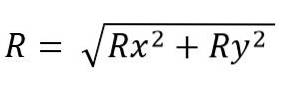
Medan för utrymme är det:
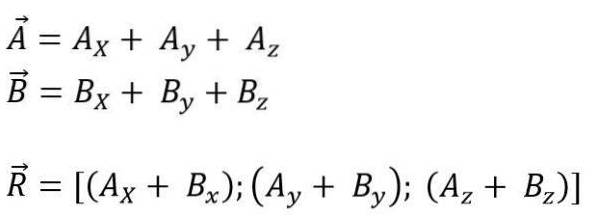
Modulen för den resulterande vektorn är:
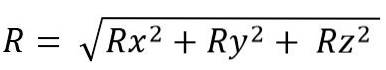
När vektorsummor utförs tillämpas flera egenskaper, vilka är:
- Associerande egenskap: den resulterande ändras inte när man lägger till två vektorer först och sedan lägger till en tredje vektor.
- Kommutativ egenskap: vektorernas ordning förändrar inte resultatet.
- Vektordistribuerande egenskap: om en skalar multipliceras med summan av två vektorer är den lika med multiplikationen av skalären med varje vektor.
- Scalar-fördelningsegenskap: om en vektor multipliceras med summan av två skalarer är den lika med multiplikationen av vektorn för varje skalar.
Multiplikation av vektorer
Multiplikationen eller produkten av vektorer kan göras som addition eller subtraktion, men att göra det på det sättet förlorar den fysiska betydelsen och finns nästan aldrig i applikationer. Därför är i allmänhet de mest använda typerna av produkter skalär- och vektorprodukten.
Scalar-produkt
Det är också känt som punktprodukten av två vektorer. När modulerna för två vektorer multipliceras med cosinus med den minsta vinkel som bildas mellan dem, erhålls en skalär. För att uttrycka en skalärprodukt mellan två vektorer placeras en punkt mellan dem och detta kan definieras som:
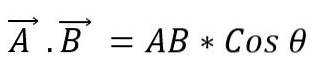
Värdet på vinkeln som finns mellan de två vektorerna beror på om de är parallella eller vinkelräta; så måste du:
- Om vektorerna är parallella och har samma avkänning, är cosinus 0º = 1.
- Om vektorerna är parallella och har motsatta riktningar är cosinus 180º = -1.
- Om vektorerna är vinkelräta är cosinus 90º = 0.
Den vinkeln kan också beräknas med vetskap om att:

Punktprodukten har följande egenskaper:
- Kommutativ egenskap: Vektorernas ordning förändrar inte skalären.
-Distributiv egenskap: om en skalar multipliceras med summan av två vektorer, är den lika med multiplikationen av skalären med varje vektor.
Vektor produkt
Vektormultiplikation, eller korsprodukt av två vektorer A och B, kommer att resultera i en ny vektor C och uttrycks med en korsning mellan vektorerna:
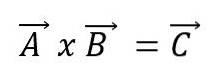
Den nya vektorn kommer att ha sina egna egenskaper. På det sättet:
- Riktningen: den här nya vektorn kommer att vara vinkelrät mot planet, vilket bestäms av originalvektorerna.
- Riktningen: detta bestäms med högerregeln, där vektorn A roteras mot B, vilket indikerar rotationsriktningen med fingrarna, och vektorn är riktad med tummen.
- Modulen: bestäms av multipliceringen av modulerna för vektorerna AxB, av sinus av den minsta vinkeln som finns mellan dessa vektorer. Det uttrycks:
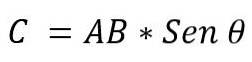
Värdet på vinkeln som finns mellan de två vektorerna beror på om de är parallella eller vinkelräta. Så det är möjligt att ange följande:
- Om vektorerna är parallella och har samma avkänning, är sinus 0º = 0.
- Om vektorerna är parallella och har motsatta riktningar, är sinus 180º = 0.
- Om vektorerna är vinkelräta är sinus 90º = 1.
När en vektorprodukt uttrycks som en funktion av dess basvektorer har vi:
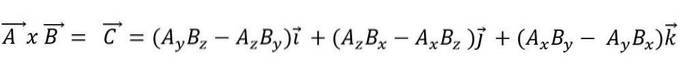
Punktprodukten har följande egenskaper:
- Det är inte kommutativt: ordningen på vektorerna förändrar skalären.
- Distributiv egenskap: om en skalar multipliceras med summan av två vektorer, är den lika med multiplikationen av skalären med varje vektor.
Referenser
- Altman Naomi, M. K. (2015). "Enkel linjär regression." Naturmetoder .
- Angel, A. R. (2007). Elementär algebra. Pearson Education,.
- Arthur Goodman, L. H. (1996). Algebra och trigonometri med analytisk geometri. Pearson Education.
- Gusiatnikov, P., & Reznichenko, S. (s.f.). Vektoralgebra i exempel. Moskva: Mir.
- Lay, D.C. (2007). Linjär algebra och dess tillämpningar. Pearson Education.
- Llinares, J. F. (2009). Linjär algebra: Vektorutrymme. Euklidiskt vektorutrymme. Alicante universitet.
- Mora, J. F. (2014). Linjär algebra. Hemland.


Ingen har kommenterat den här artikeln än.