
Fermat begränsar vad den består av och övningar löst
De Fermat-gräns är en numerisk metod som används för att få värdet av en linjes lutning, som är tangent till en funktion vid en given punkt i dess domän. Den används också för att erhålla kritiska punkter i en funktion. Dess uttryck definieras som:
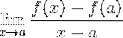
Det är uppenbart att Fermat inte kände till grunderna för härledning, men det var hans studier som fick en grupp matematiker att fråga om tangentlinjer och deras tillämpningar i kalkyl..
Artikelindex
- 1 Vad är Fermat-gränsen??
- 2 Tillämpning av Fermat-gränsen för maxima och minima
- 2.1 Den kubiska parabolen
- 2.2 Maximalt och minimalt
- 2.3 Metod
- 3 Historia
- 4 Övningar
- 4.1 Övning 1
- 4.2 Övning 2
- 5 Referenser
Vad är Fermat-gränsen??

Den består av ett tillvägagångssätt på två punkter, som i tidigare förhållanden bildar en sekantlinje till funktionen med skärningspunkt i par av värden.
Genom att närma sig variabeln till värdet "a" tvingas poängparet att mötas. På detta sätt blir den tidigare sekanta linjen tangent till punkten (a; f (a)).
Värdet på kvoten (x - a), när den utvärderas vid punkten "a", ger en obestämbarhet av K-typgränser mellan noll (K / 0). Där dessa olika bestämningar kan brytas genom olika faktureringstekniker.
De vanligaste användningsteknikerna är:
-Skillnad mellan rutor (atvå - btvå ) = (a + b) (a - b); Elementets existens (a-b) antyder i de flesta fall den faktor som förenklar uttrycket (x-a) i kvoten för Fermat-gränsen.
- Slutförande av rutor (axtvå + bx); Efter att ha avslutat rutor erhålls ett Newton binomium, där en av dess två faktorer förenklas med uttrycket (x - a), vilket bryter obestämligheten.
- Konjugat (a + b) / (a + b); Att multiplicera och dela uttrycket med konjugatet av någon faktor kan vara till stor hjälp för att bryta obestämdheten.
- Vanlig faktor; I många fall döljer resultatet av manövreringen av Fermat-gränsen f (x) - f (a) den faktor (x - a) som är nödvändig för att faktor. För detta observeras noggrant vilka element som upprepas i varje faktor i uttrycket.
Tillämpning av Fermat-gränsen för maximum och minimum
Även om Fermat-gränsen inte skiljer mellan maximalt och minimum, eftersom det bara kan identifiera de kritiska punkterna enligt dess definition, används det vanligtvis vid beräkning av lock eller golv för funktionerna i planet..
En grundläggande kunskap om den grafiska funktionsteorin i samband med denna sats kan vara tillräcklig för att fastställa maximala och minimala värden mellan funktioner. Faktum är att böjningspunkterna kan definieras med hjälp av medelvärdessatsen utöver Fermats sats.
Den kubiska parabolen
Den viktigaste paradoxen för Fermat kom från att studera den kubiska parabolen. Eftersom hans uppmärksamhet riktades mot tangentlinjerna för en funktion för en given punkt, stötte han på problemet med att definiera tangentlinjen vid böjningspunkten i funktionen.
Det verkade omöjligt att bestämma tangentlinjen till en punkt. Således börjar förfrågan som skulle ge upphov till differentialräkningen. Definieras senare av viktiga matematiska exponenter.
Maximus och minimalt
Studien av maximala och minsta för en funktion var en utmaning för klassisk matematik, där en entydig och praktisk metod behövdes för att definiera dessa.
Fermat skapade en metod baserad på driften av små differentiella värden, som efter factoring-processer elimineras, vilket viker för det maximala och minimala värdet som söks.
Denna variabel måste utvärderas i det ursprungliga uttrycket för att bestämma koordinaten för nämnda punkt, som tillsammans med analytiska kriterier kommer att definieras som det maximala eller minsta av uttrycket.
Metod
I sin metod använder Fermat den bokstavliga symboliken i Vieta, som bestod i exklusiv användning av stora bokstäver: vokaler, för okända och konsonanter för kända mängder..
För fallet med radikala värden implementerade Fermat en viss process, som senare skulle användas i faktorisering av gränserna för obestämdhet oändlighet bland oändlighet.
Denna process består av att dela varje uttryck med värdet på den differentiella som används. I fallet Fermat använde han bokstaven E, där efter att ha delat med den högsta makten i E blir det värde som söks för den kritiska punkten tydligt..
Berättelse
Fermat-gränsen är faktiskt ett av de minst kända bidraget i matematikerns långa lista. Hans studier gick från primtal för att i grunden skapa baserna för beräkningen.
I sin tur var Fermat känd för sina excentriciteter angående hans hypoteser. Det var vanligt för honom att lämna en slags utmaning till de andra matematikerna då, när han redan hade lösningen eller beviset.
Han hade en stor variation av tvister och allianser med olika tidens matematiker, som älskade eller hatade att arbeta med honom.
Hans sista sats var huvudansvarig för hans världsberömmelse, där han uppgav att en generalisering av Pythagoras sats för alla betyg "n" var det omöjligt. Han påstod sig ha ett giltigt bevis på det, men dog innan han offentliggjorde det.
Denna demonstration fick vänta cirka 350 år. 1995 gjorde matematikerna Andrew Wiles och Richard Taylor ett slut på den ångest som Fermat lämnade och visade att han hade rätt genom ett giltigt bevis på sin sista sats..
Träning
Övning 1
Definiera lutningen för tangentlinjen till kurvan f (x) = xtvå vid punkten (4, 16)
Att ersätta uttrycket för Fermat-gränsen har vi:
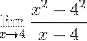
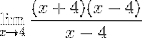
Faktorerna (x - 4) förenklas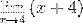
När du utvärderar har du
M = 4 + 4 = 8
Övning 2
Definiera den kritiska punkten för uttrycket f (x) = xtvå + 4x med Fermat-gränsen
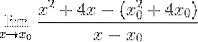
En strategisk gruppering av element genomförs för att gruppera X-X-paren0
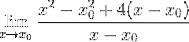
De minsta kvadraterna utvecklas
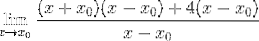
Den gemensamma faktorn X-X observeras0 och extraheras
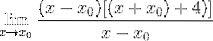
Uttrycket kan nu förenklas och obestämligheten brytas
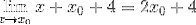
Vid minimipunkterna är det känt att tangentlinjens lutning är lika med noll. På detta sätt kan vi utjämna uttrycket som hittas till noll och lösa värdet X0
2 X0 + 4 = 0
X0 = -4/2 = -2
För att få den saknade koordinaten är det bara nödvändigt att utvärdera punkten i den ursprungliga funktionen
F (-2) = (-2)två + 4 (-2) = 4-8 = - 4
Den kritiska punkten är P (-2, -4).
Referenser
- Verklig analys. En historisk strategi Sauhl Stahl, John Wiley & Sons, 5 aug. 1999.
- The Mathematical Career of Pierre de Fermat, 1601-1665: Second Edition. Michael Sean Mahoney. Princeton University Press, 5 juni. 2018
- Från Fermat till Minkowski: Föreläsningar om talteorin och dess historiska utveckling. W. Scharlau, H. Opolka, Springer Science & Business Media, 1985
- Fermats sista sats: En genetisk introduktion till algebraisk talteori. Harold M. Edwards. Springer Science & Business Media, 14 jan 2000
- Fermatdagar 85: Matematik för optimering. J B. Hiriart-Urruty Elsevier, 1 jan. 1986

Ingen har kommenterat den här artikeln än.