
Kvantmekanisk modell av atombeteendet, exempel
De kvantmekanisk modell av atomen antar att detta bildas av en central kärna som består av protoner och neutroner. Negativt laddade elektroner omger kärnan i diffusa regioner som kallas orbitaler..
Formen och omfattningen av elektroniska orbitaler bestäms av olika storheter: kärnans potential och de kvantiserade energinivåerna och elektronernas vinkelmoment.
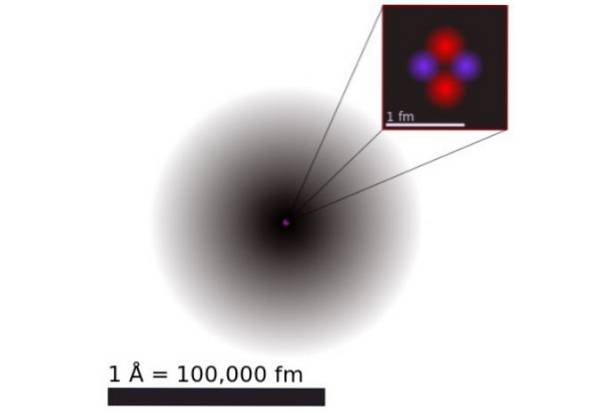
Enligt kvantmekanik har elektroner dubbelt vågpartikelbeteende och i atomskala är de diffusa och icke-punktiska. Atomens dimensioner bestäms praktiskt taget av förlängningen av de elektroniska orbitalerna som omger den positiva kärnan.
Figur 1 visar strukturen för heliumatomen, som har en kärna med två protoner och två neutroner. Denna kärna omges av sannolikhetsmolnet för de två elektronerna som omger kärnan, vilket är hundratusen gånger mindre. I följande bild kan du se heliumatomen, med protonerna och neutronerna i kärnan och elektronerna i orbitaler.

Storleken på en heliumatom är i storleksordningen en ångström (1 Å), det vill säga 1 x 10 ^ -10 m. Medan storleken på dess kärna är i storleksordningen a femtometer (1 fm), det vill säga 1 x 10 ^ -15 m.
Trots att den är så relativt liten koncentreras 99,9% av atomvikten i den lilla kärnan. Detta beror på att protonerna och neutronerna är 2000 gånger tyngre än elektronerna som omger dem..
Artikelindex
- 1 Atomskala och kvantbeteende
- 1.1 Första kvantmodeller
- 2 Dynamik av materialvågor
- 2.1 Atomiska orbitaler
- 2.2 Kvantnummer
- 3 Orbitalernas form och storlek
- 3.1 Snurrningen
- 4 Referenser
Atomskala och kvantbeteende
Ett av de begrepp som hade störst inflytande på utvecklingen av atommodellen var dualiteten våg - partikel: upptäckten att varje materiellt objekt har en materia-våg associerad med sig.
Formeln för beräkning av våglängden λ associerad med ett materiellt objekt föreslogs av Louis De Broglie 1924 och är följande:
λ = h / (m v)
Var h är Plancks konstant, m degen och v hastighet.
Enligt De Broglies princip har varje objekt ett dubbelt beteende, men beroende på interaktionsskalan, hastigheten och massan kan vågbeteendet vara mer framträdande än partikelbeteendet eller vice versa..
Elektronen är lätt, dess massa är 9,1 × 10 ^ -31 kg. Den elektroniska hastigheten för en elektron är 6000 km / s (femtio gånger långsammare än ljusets hastighet). Denna hastighet motsvarar energivärden inom intervallet tiotals elektronvolt..
Med ovanstående data och med hjälp av de Broglie-formeln kan våglängden för elektronen erhållas:
λ = 6,6 x 10 ^ -34 J s / (9,1 × 10 ^ -31 kg 6 x 10 ^ 6 m / s) = 1 x 10 ^ -10 m = 1 Å
Elektronen vid atomnivåernas typiska energier har en våglängd av samma storleksordning som atomskalans, så att den i den skalan har ett vågbeteende och inte en partikel..
Första kvantmodeller
Med tanke på att atomskalelektronen har vågbeteende utvecklades de första atommodellerna baserade på kvantprinciper. Bland dessa utmärker sig Bohr-atommodellen, som perfekt förutspådde vätgasemissionsspektrumet, men inte det för andra atomer.
Bohr-modellen och senare Sommerfeld-modellen var halvklassiska modeller. Det vill säga elektronen behandlades som en partikel som utsattes för den elektrostatiska attraktionskraften hos kärnan som kretsade kring den, styrd av Newtons andra lag..
Förutom klassiska banor tog dessa första modeller hänsyn till att elektronen hade en tillhörande materialvåg. Endast banor vars omkrets var ett heltal våglängder tillåts, eftersom de som inte uppfyller detta kriterium försvinner av destruktiv störning..
Det är då som kvantiseringen av energi visas för första gången i atomstrukturen..
Ordet kvant Det kommer just från det faktum att elektronen bara kan ta på sig vissa diskreta energivärden inom atomen. Detta sammanfaller med Plancks upptäckt, som bestod i upptäckten att en strålning av frekvens F interagerar med materia i energipaket E = h f, var h är Plancks konstant.
Materialvågornas dynamik
Det fanns inte längre något tvivel om att elektronen på atomnivå beter sig som en materialvåg. Nästa steg var att hitta ekvationen som styr deras beteende. Den ekvationen är varken mer eller mindre än Schrodinger-ekvationen, som föreslogs 1925.
Denna ekvation relaterar till och bestämmer vågfunktionen ψ associerad med en partikel, såsom elektronen, med dess interaktionspotential och dess totala energi OCH. Dess matematiska uttryck är:


Jämlikhet i Schrodinger-ekvationen gäller endast för vissa värden av den totala energin OCH, ger upphov till kvantisering av energi. Vågfunktionen för elektronerna som utsätts för kärnans potential erhålls från lösningen av Schrodinger-ekvationen.
Atomiska orbitaler
Det absoluta värdet för vågfunktionen i kvadrat |ψ| ^ 2, ger sannolikhetsamplituden för att hitta elektronen vid en given position.
Detta leder till begreppet orbital, som definieras som det diffusa området som upptas av elektronen med icke-noll sannolikhetsamplitud, för de diskreta värdena för energi och vinkelmoment bestämda av lösningarna i Schrodinger-ekvationen.
Kunskapen om orbitalerna är mycket viktig eftersom den beskriver atomstrukturen, den kemiska reaktiviteten och de möjliga bindningarna för att bilda molekyler.
Väteatomen är den enklaste av alla, eftersom den har en ensam elektron och den är den enda som medger en exakt analytisk lösning av Schrodinger-ekvationen.
Denna enkla atom har en kärna som består av en proton, som producerar en central potential för Coulomb-attraktion som bara beror på radien. r, så det är ett system med sfärisk symmetri.
Vågfunktionen beror på positionen som ges av de sfäriska koordinaterna i förhållande till kärnan, eftersom den elektriska potentialen har central symmetri.
Dessutom kan vågfunktionen skrivas som en produkt av en funktion som bara beror på den radiella koordinaten, och en annan som beror på vinkelkoordinaterna:

Kvantnummer
Lösningen av den radiella ekvationen ger de diskreta energivärdena, som beror på ett heltal n, ringde huvudkvantnummer, som kan ta positiva heltal värden 1, 2, 3, ...
Diskreta energivärden är negativa värden som ges med följande formel:

Vinkelekvationslösningen definierar de kvantiserade värdena för vinkelmomentet och dess z-komponent, vilket ger upphov till kvantantal l Y ml.
Kvantantalet av vinkelmoment l går från 0 till n-1. Kvantnummer ml kallas magnetiskt kvantnummer och går från -l fram tills +l. Till exempel ja l var 2 skulle det magnetiska kvantantalet ta värdena -2, -1, 0, 1, 2.
Orbitalernas form och storlek
Orbitalens radiella räckvidd bestäms av radivågfunktiontill. Det är större när elektronens energi ökar, det vill säga när huvudkvantantalet ökar.
Det radiella avståndet mäts vanligtvis i Bohr-radier, som för den lägsta energin av väte är 5,3 X 10-11 m = 0,53 Å.

Men formen på orbitalerna bestäms av värdet av det vinkelmomentkvantala antalet. Om l = 0 har vi en sfärisk bana som heter s, om l = 1 har vi en lobulerad bana som heter sid, som kan ha tre riktningar enligt det magnetiska kvantantalet. Följande bild visar orbitalernas form.
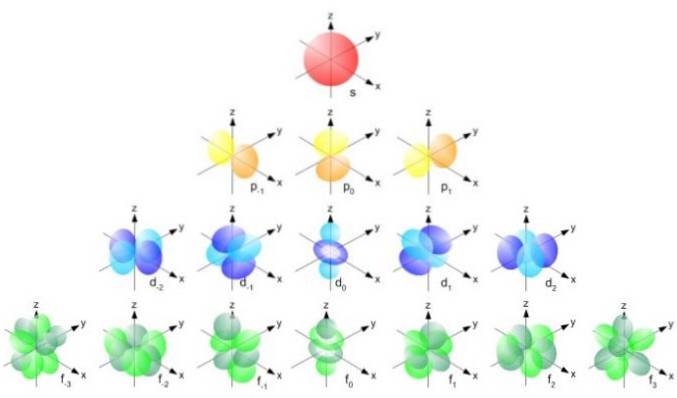
Dessa orbitaler packas in i varandra enligt elektronernas energi. Till exempel visar följande bild orbitalerna i en natriumatom.
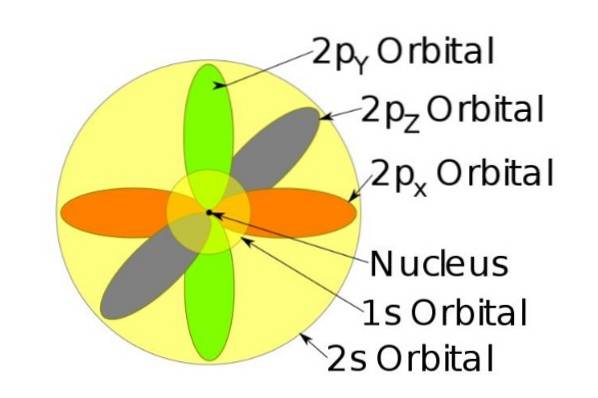
Snurrningen
Den kvantmekaniska modellen för Schrödinger-ekvationen innehåller inte elektronens snurrning. Men det beaktas genom Pauli-uteslutningsprincipen, som indikerar att orbitaler kan fyllas med upp till två elektroner med centrifugeringskvantum s = + ½ och s = -½.
Till exempel har natriumjonen 10 elektroner, det vill säga om vi hänvisar till föregående figur, finns det två elektroner för varje omlopp.
Men om det är den neutrala natriumatomen finns det 11 elektroner, varav den sista skulle uppta en 3s-omlopp (visas inte i figuren och med en större radie än 2s). Atons snurrning är avgörande för ett ämnes magnetiska egenskaper.
Referenser
- Alonso - Finn. Kvant- och statistikgrund. Addison Wesley.
- Eisberg - Resnick. Kvantfysik. Limusa - Wiley.
- Gasiorowicz. Kvantfysik. John Wiley & Sons.
- HSC. Fysik kurs 2. Jacaranda plus.
- Wikipedia. Schrodingers atommodell. Återställd från: Wikipedia.com


Ingen har kommenterat den här artikeln än.