
Pendelrörelse
Vad är pendelrörelsen?
De pendelrörelse Det är en fram och tillbaka rörelse gjord av ett mer eller mindre tungt föremål, kallat en pendel, upphängd av ett rep eller ljusstav, fixerad i sin andra ände.
Pendeln får en initial impuls och får svänga, på detta sätt beskriver objektet bågar fram och tillbaka. Detta är principen om hur pendelklockor, gungor, gungstolar och metronomer pendel, används för att markera tiderna i musik.
Det sägs att omkring 1581 observerade Galileo Galilei svängningen av en lampa i katedralen i Pisa och observerade att, även om amplituden för ljuskronans svängning minskade på grund av friktion med luften, inte lampans varaktighet..
Detta fick Galileos uppmärksamhet, som bestämde sig för att fortsätta med studien och bestämde att pendelns period inte beror på massan utan på kvadratroten på ackordets längd, vilket kommer att ses senare..
Pendelrörelseegenskaper
En pendel är väldigt lätt att bygga, eftersom det räcker med en lodlinje som hänger från en bomullstråd och hålls fast i den andra änden med fingrarna eller genom att fästa den på ett stöd som en spik..
Efter den lilla initiala impulsen ansvarar vikten för att hålla pendeln oscillerande, även om friktionen minskar rörelsens amplitud tills den slutligen upphör helt..
Huvudegenskapen för pendelrörelsen är att vara repetitiv, eftersom det är en fram och tillbaka rörelse. För att underlätta studien är det enkelt att göra några förenklingar för att fokusera på en enklare modell, kallad enkel pendel.
Den enkla pendeln

Det är ett idealiskt system som består av en lodlinje, betraktad som en punktmassa m, fäst vid ett lätt, osträckbart längdrep L. Egenskaperna hos detta system är:
- Ha en repetitiv och periodisk rörelse, bestående av att gå fram och tillbaka en båge med radieomkrets lika med L.
- Tar inte hänsyn till friktion.
- Rörelseomfånget är litet (< 5º).
- Perioden är oberoende av massan m, och beror enbart på längden L pendel.
Formler och ekvationer
Följande är ett diagram över den enkla pendeln, på vilken två krafter verkar: vikten P med magnitud mg, som riktas vertikalt nedåt och spänningen T På repet. Friktion beaktas inte.
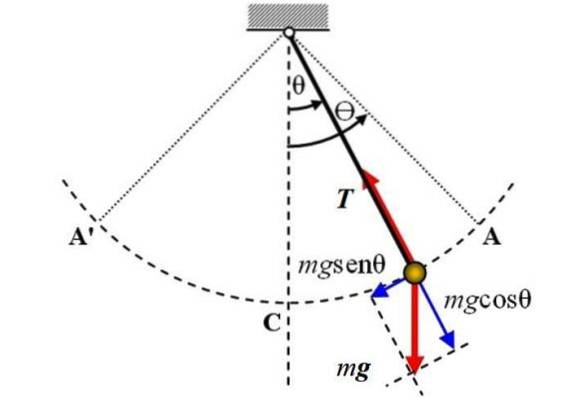
Referensaxeln är den vertikala axeln och sammanfaller med positionen θ = 0, därifrån mäts vinkelförskjutningen,, antingen i en eller annan riktning. + -Tecknet kan tilldelas till höger skift i figuren.
För att studera pendelns rörelse väljs ett koordinatsystem med ursprunget vid själva pendeln. Detta system har en tangentiell koordinat till omkretsbågen A'CA som beskrivs av pendeln, liksom en radiell koordinat, riktad mot centrum av banan..
I det ögonblick som visas i figuren rör sig pendeln åt höger, men den tangentiella gravitationskomponenten, kallad Ft, är ansvarig för att få honom att återvända. Det framgår av figuren att denna komponent har motsatt riktning mot rörelse.
När det gäller spänningen i repet är det balanserat med komponenten i vikten mgcosθ.

Vinkelförskjutning
Vi måste uttrycka ekvationen i termer av en enda variabel och komma ihåg att vinkelförskjutningen θ och den böjda bågen är relaterade till ekvationen:
s = L.θ
Massan avbryts på båda sidor och om amplituden är liten, kommer vinkeln θ också, så följande approximation är giltig:
sen θ ≈ θ
Med detta erhålls följande differentialekvation för variabeln θ (t):


Denna ekvation är mycket lätt att lösa, eftersom dess lösning är en funktion vars andra derivat är själva funktionen. Det finns tre alternativ: en cosinus, en sinus eller en exponentiell. Cosinusfunktionen väljs för vinkelförskjutningen θ (t), eftersom den är en välkänd och lätt att hantera funktion.
Läsaren kan verifiera, genom att skilja två gånger, att följande funktion uppfyller differentialekvationen:
θ (t) = θm cos (ωt + φ)
Var θm är den maximala vinkeln som pendeln rör sig med avseende på vertikalen och vinkelfrekvensen ω är:

Periodens ekvation
Perioden T för rörelsen är den tid det tar att utföra en cykel och definieras som:

Ersätter ω:

Som nämnts ovan beror perioden inte på pendelns massa utan bara på dess längd..
Exempel på pendelrörelse
Pulsmätning
Galileo hade tanken att mäta hjärtfrekvensen hos människor, justera pendelns längd så att perioden sammanföll med hjärtslag..
Pendelklockan
Detta är utan tvekan ett av de mest kända exemplen på pendelrörelse. Pendelklocktillverkning handlar lika mycket om vetenskap som om konst. Den holländska fysikern Christian Huygens (1629-1695) utvecklade den första pendelklockan 1656, baserat på den studie som gjordes för flera år sedan av Galileo.
Foucaults pendel

Det är en något annan pendel än den som beskrivs ovan, eftersom den kan rotera i vilket vertikalt plan som helst. Den skapades av den franska fysikern Léon Foucault (1819-1868) och används för att visualisera jordens rotation.
Övningen löst
En enkel pendel passerar var 0,5: e sekund genom jämviktspositionen. Hur lång är tråden?
Lösning
Eftersom perioden är den tid det tar att slutföra en fullständig cykel, där den passerar genom jämviktspositionen två gånger: den ena går och den andra tillbaka, sedan:
T = 2 × 0,5 s = 1 s
Från:

Trådens längd L rensas:

Tråden är 0,25 m eller 25 cm lång.
Referenser
- Figueroa, D. (2005). Serie: Fysik för vetenskap och teknik. Volym 2. Dynamik. Redigerad av Douglas Figueroa (USB).
- Giambattista, A. 2010. Fysik. 2: a. Ed McGraw Hill.
- Giancoli, D. 2006. Fysik: principer med tillämpningar. 6: e. Ed prentice hall.
- Katz, D. 2013. Fysik för forskare och ingenjörer. Grunder och anslutningar. Cengage Learning.
- Knight, R. 2017. Physics for Scientists and Engineering: a Strategy Approach. Pearson.


Ingen har kommenterat den här artikeln än.