
Dubbel provtagning


Vad är dubbel provtagning?
De dubbelprovtagning är en teknik som används i slutlig statistik när du vill veta mer detaljer och säkerhet om en viss variabel, som kännetecknar en viss population.
Det andra populationsprovet utförs i allmänhet efter att ett första prov har tagits och analyserats, vars analys inte gav någon statistiskt signifikant slutsats på någon av studievariablerna..
Av denna anledning är dubbelprovtagning i statistik också känd som provtagning i två steg. Nyttan med det andra provet är att det hjälper till att med större precision bestämma uppskattningen av förhållanden och regressioner för en viss hjälpvariabel, som uppstår mot bakgrund av analysen av ett första prov..
En annan användning som ges för dubbelprovtagning är att samla in information för att genomföra ett provtagning efter skikt..
Exempel
Olika situationer där dubbel provtagning är motiverad kommer att beskrivas nedan..
Kvalitetskontroll vid produktion av delar
Den dubbla provtagningsmetoden används ofta i industriell kvalitetskontroll och görs vanligtvis i två faser..
Antag till exempel en industriell maskin som tillverkar vissa delar. Oavsett hur mycket maskinen justeras är ingen del identisk med en annan eftersom små variationer kan förekomma i dess mått och vikt. Det handlar om att avgöra om en sats av delar som tillverkas av maskinen uppfyller toleranskriterierna för att den ska accepteras eller avvisas..
Först tas ett slumpmässigt urval av bitar som du vill kontrollera om en av variablerna, till exempel bitens längd, ligger inom tolerans.
I händelse av att den genomsnittliga längden är under eller över den önskade toleransgraden för nämnda variabel, i detta första prov, sluts det att partiet är defekt och det måste kasseras. I detta fall krävs inga nya prover.
Omvänt, om medelvärdet ligger inom toleransområdet, men standardavvikelsen för provet är tillräckligt stor för att adderingen eller subtraheringen av medelvärdet faller utanför intervallet, så måste ett andra större prov samlas in..
Detta andra urval måste inkludera det ursprungliga urvalet för att göra om beräkningarna och därmed kunna fatta ett slutgiltigt beslut angående den undersökta variabeln. På detta sätt kan det vara känt om partiet är defekt eller inte.
Lägre provtagningskostnader
Vid många tillfällen är informationen om en av variablerna som ska studeras svår att komma åt. Men det kan finnas en hjälpvariabel lättare för datainsamling.
I detta fall tas två prover, ett stort för hjälpvariabeln, billigare och ett mindre prov, som ingår i det större provet av den dyraste variabeln..
Denna metod är tillämplig när det bestäms att det finns en korrelation mellan båda variablerna, vilket i allmänhet är ett proportionellt förhållande..
Ett exempel på denna situation förekommer inom skogsvetenskap, där man önskar bestämma andelen träd som påverkas av en parasitväxt (ringorm).
Eftersom dessa är mycket omfattande regioner och svåra att komma åt är det inte möjligt att studera den totala populationen av träd i tid och kostnader. Dessa steg följs sedan:
Steg 1: ta prover
Ett preliminärt provtagning skulle bestå av användning av flygfotografering och skogen är indelad i partier. Härifrån väljs några slumpmässigt slumpmässigt och det uppskattas, genom att analysera bilderna på de valda partierna, hur många träd som påverkas av ringmask, eftersom trädens färg påverkas av parasiten..
Steg 2: Fältarbete
Men den fotografiska analysen kan vara felaktig, så några satser av det första provet väljs, helst slumpmässigt, för att utföra fältarbete..
Steg 3: jämförelse
Fältresultatet jämförs sedan med det fotografiska för avlyssning av de två satserna. Denna jämförelse kan exempelvis utföras genom att skapa ett diagram där den horisontella axeln är det värde som erhålls för varje sats genom fotografering och på den vertikala axeln det värde som erhålls per sats genom fältarbete..
Denna grafiska metod gör det möjligt att visuellt identifiera huruvida det finns en korrelation mellan båda resultaten och att genom en regressionsanalys bestämma proportionalitetskoefficienten eller förhållandet mellan båda proverna..
Efter det största urvalet, det vill säga det fotografiska provet, tas medelvärdet av infekterade träd och deras standardavvikelse. Men eftersom proportionalitetskoefficienten och dess fel med fältproverna bestämdes, är det möjligt att korrigera resultatet av det större provet (det fotografiska).
Detta resultat kan sedan extrapoleras till hela trädpopulationen.
Fördelar och nackdelar med dubbelprovtagning
I de beskrivna exemplen är kostnadsfördelen uppenbar, eftersom det sparar tid och pengar att ersätta en lättillgänglig variabel med en annan som är svåråtkomlig..
En nackdel är att i fallet med dubbelprovtagning för kvalitetskontroll finns det en risk att gå igenom bra satser av produkter som inte är toleranta..
Övning
Vi vill uppskatta antalet sjuka träd i en 162 hektar stor skog. Eftersom skogen är mycket omfattande är den uppdelad i 100 paket av samma område. 18 tomter väljs slumpmässigt och med hjälp av en fotografisk undersökning uppskattas det att i dessa 18 tomter finns 8,5 sjuka träd med ett standardfel på plus eller minus 4,5 träd.
Från dessa 18 tomter väljs slumpmässigt 8 tomter där fältstudien genomförs. För dessa åtta tomter visar den fotografiska studien 10 sjuka träd med ett fel på plus eller minus 5,3 träd..
Å andra sidan, för samma åtta tomter visar fältstudien 12,4 sjuka träd med ett fel på plus minus 6,3 träd.
Det frågar:
- a) Bestäm proportionalitetskoefficienten mellan fältstudien genom linjär regression.
- b) Uppskatta antalet sjuka träd med hjälp av den fotografiska metoden i de hundra tomterna.
- c) Använd korrigeringen med den erhållna proportionalitetskoefficienten för att uppskatta det verkliga antalet sjuka träd i hela skogen.
Lösning
En graf görs av antalet träd per fotografiskt antal kontra fälträkning för de åtta partier som valts för båda studierna..
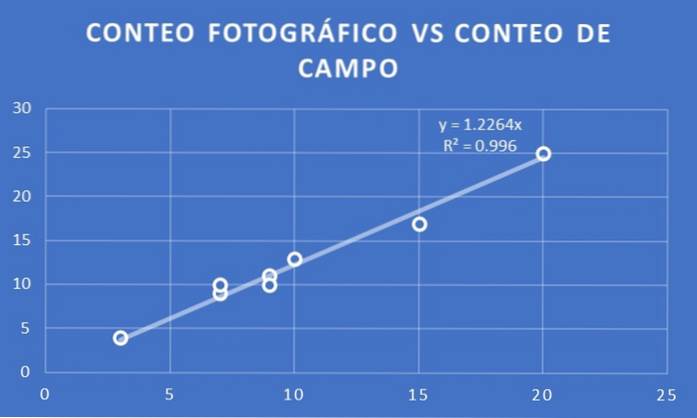
En trendlinje är monterad och dess lutning bestäms. I detta fall erhålls att proportionalitetskoefficienten är 1,23. Det vill säga, om X är antalet per fotografiskt antal, uppskattas det att fältantalet blir Y = 1,23 X.
Antalet sjuka träd enligt fotografiskt antal i de 18 utvalda partierna kommer att vara:
18 x 8,5 = 153
Men eftersom hela skogen var uppdelad i 100 tomter av samma område är antalet sjuka träd uppskattat med den fotografiska metoden: (100/18) x 153 = 850.
Korrektionsfaktorn som erhållits från jämförelsen mellan fält- och fotografistudien tillämpas nu:
Uppskattat faktiskt antal sjuka träd i skogen = 1,23 x 850 = 1046.
Referenser
- Dubbelprovtagning för förhållande uppskattning, PennState College. Återställd från psu.edu
- Dubbel, multipel och sekventiell provtagning, NC State University. Återställd från ncsu.edu
- Enkel slumpmässig provtagning. Återställd från investopedia.com
- Vad är dubbelprovtagning? Återställd från: nist.gov
- Provtagning. Återställd från: en.wikipedia.org
- Flerstegssampling. Återställd från: en.wikipedia.org


Ingen har kommenterat den här artikeln än.