
Sinusvågegenskaper, delar, beräkning, exempel
De sinusvågor De är vågmönster som kan beskrivas matematiskt med sinus- och cosinusfunktionerna. De beskriver exakt naturhändelser och tidsvarierande signaler, såsom spänningar som genereras av kraftverk och sedan används i hem, industrier och gator.
Elektriska element som motstånd, kondensatorer och induktanser, som är anslutna till sinusformade spänningsingångar, ger också sinusformade svar. Matematiken som används i beskrivningen är relativt enkel och har studerats grundligt..

Matematiken för sinus- eller sinusformade vågor, som de också är kända, är den för sinus- och cosinusfunktionerna.
Dessa är repetitiva funktioner, vilket betyder periodicitet. Båda har samma form, förutom att cosinus flyttas åt vänster med avseende på sinus med en fjärdedel av en cykel. Det kan ses i figur 2:

Då cos x = sin (x + π / 2). Med hjälp av dessa funktioner representeras en sinusvåg. För att göra detta placeras storleken i fråga på den vertikala axeln, medan tiden ligger på den horisontella axeln..
Diagrammet ovan visar också den repetitiva kvaliteten på dessa funktioner: mönstret upprepar sig kontinuerligt och regelbundet. Tack vare dessa funktioner är det möjligt att uttrycka sinusformade spänningar och strömmar varierande i tid, placera dem på den vertikala axeln istället för Y, a v eller en i för att representera spänning eller ström och på den horisontella axeln istället för x, de t väder.
Det mest allmänna sättet att uttrycka en sinusvåg är:
v (t) = vm sen (ωt + φ)
Sedan kommer vi att gräva i innebörden av detta uttryck, definiera några grundläggande termer för att karakterisera sinusvågen.
Artikelindex
- 1 delar
- 1.1 Period
- 1.2 Amplitud
- 1.3 Cykel
- 1.4 Frekvens
- 1.5 Fas
- 2 Sinusgenerator
- 2.1 Tillämpning av Faradays lag
- 2.2 Wien-oscillator
- 3 Hur man beräknar sinusvågor?
- 3.1 Oscilloskopet
- 4 Exempel
- 4.1 Exempel 1
- 4.2 Exempel 2
- 5 Referenser
Delar
Period, amplitud, frekvens, cykel och fas är begrepp som tillämpas på periodiska eller repetitiva vågor och är viktiga för att karakterisera dem ordentligt..
Period
En periodisk funktion som de nämnda, som upprepas med jämna mellanrum, uppfyller alltid följande egenskaper:
f (t) = f (t + T) = f (t + 2T) = f (t + 3T) = ... .
Var T är en kvantitet som kallas vågperiod, y är den tid det tar att upprepa en fas av samma. I internationella systemenheter mäts perioden i sekunder.
Amplitud
Enligt det allmänna uttrycket för sinusvåg v (t) = vm sin (ωt + φ), vm är det maximala värdet för funktionen, som inträffar när sin (ωt + φ) = 1 (kom ihåg att det största värdet som både sinus- och cosinusfunktionerna medger är 1). Detta maximala värde är exakt vågamplitud, också känd som toppamplitud.
Vid en spänning kommer den att mätas i volt och om den är en ström kommer den att vara i ampere. I den visade sinusvågen är amplituden konstant, men i andra typer av vågor kan amplituden variera.
Cykel
Det är en del av vågen som ingår i en period. I föregående figur togs perioden genom att mäta den från två på varandra följande toppar eller toppar, men den kan börja mätas från andra vågpunkter, så länge de är begränsade av en period.
Observera i följande bild hur en cykel täcker från en punkt till en annan med samma värde (höjd) och samma lutning (lutning).
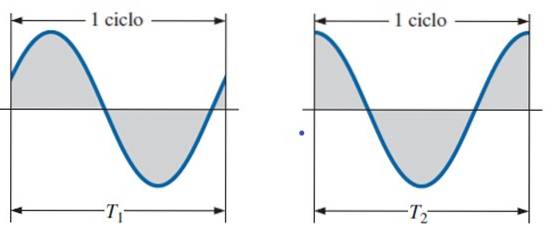
Frekvens
Det är antalet cykler som inträffar på en sekund och är kopplat till sinusfunktionens argument: .t. Frekvensen betecknas som F och mäts i cykler per sekund eller Hertz (Hz) i International System.
Frekvensen är periodens omvända mängd, därför:
f = 1 / T.
Medan frekvensen F är relaterat till vinkelfrekvens ω (pulsering) såsom:
ω = 2πF
Vinkelfrekvensen uttrycks i radianer / sekund i det internationella systemet, men radianerna är dimensionella, så frekvensen F och vinkelfrekvensen ω de har samma dimensioner. Observera att produkten .t ger radianer som ett resultat och måste tas med i beräkningen när du använder miniräknaren för att få värdet av sen ωt.
Fas
Det motsvarar den horisontella förskjutningen som vågen upplever med avseende på en tid som referens.
I följande bild ligger den gröna vågen en gång före den röda vågen td. Två sinusvågor är inne fas när dess frekvens och fas är desamma. Om fasen skiljer sig är de i glipa. Vågorna i figur 2 är också ur fas.
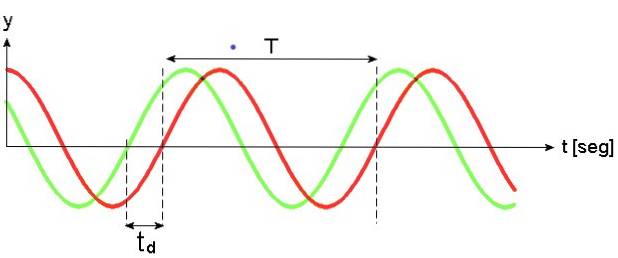
Om frekvensen för vågorna är annorlunda kommer de att vara i fas när fasen ωt + φ är densamma i båda vågorna vid vissa tider.
Sinusgenerator
Det finns många sätt att få en sinusvågssignal. Hemuttag ger dem.
Faradays brottsbekämpning
Ett ganska enkelt sätt att få en sinusformad signal är att använda Faradays lag. Detta indikerar att i en sluten strömkrets, till exempel en slinga, placerad mitt i ett magnetfält, genereras en inducerad ström när magnetfältets flöde genom den ändras i tid. Följaktligen, a inducerad spänning eller inducerad emf.
Flödet av magnetfältet varierar om slingan roteras med konstant vinkelhastighet mitt i fältet skapat mellan N- och S-polerna på magneten som visas i figuren..
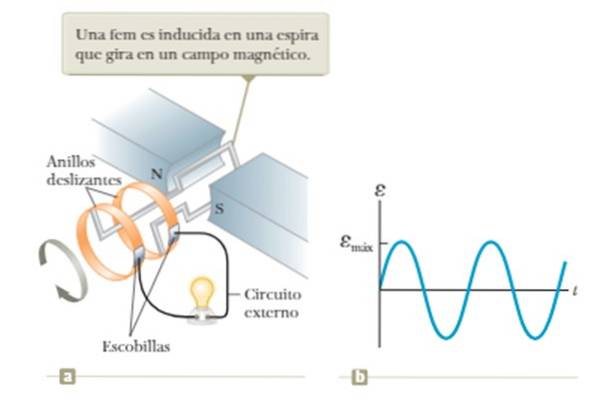
Begränsningen av denna anordning är beroendet av den spänning som erhålls med slingans rotationsfrekvens, vilket kommer att ses mer detaljerat i exempel 1 i avsnittet nedan..
Wien Oscillator
Ett annat sätt att få en sinusvåg, den här gången med elektronik, är via Wien-oscillatorn, som kräver en operationsförstärkare i anslutning till motstånd och kondensatorer. På detta sätt erhålls sinusvågor vars frekvens och amplitud användaren kan ändra enligt deras bekvämlighet genom att justera med omkopplare..
Figuren visar en sinusformad signalgenerator, med vilken andra vågformer också kan erhållas: bland annat triangulär och kvadratisk..

Hur man beräknar sinusvågor?
För att utföra beräkningar som involverar sinusvågor används en vetenskaplig räknare som har de trigonometriska funktionerna sinus och cosinus, liksom deras inverser. Dessa räknare har lägen för att arbeta vinklarna antingen i grader eller i radianer, och det är lätt att konvertera från en form till en annan. Omvandlingsfaktorn är:
180 º = π radianer.
Beroende på kalkylatormodellen måste du navigera med MODE-tangenten för att hitta DEGREE-alternativet, som låter dig arbeta trigonometriska funktioner i grader, eller RAD-alternativet, för att direkt arbeta vinklarna i radianer.
Till exempel sin 25º = 0,4226 med miniräknaren inställd på DEG-läge. Omvandling av 25º till radianer ger 0,4363 radianer och sin 0,4363 rad = 0,425889 ≈ 0,4226.
Oscilloskopet
Oscilloskopet är en anordning som gör att både direkt- och växelspännings- och strömsignaler kan visas på en skärm. Den har vred för att justera storleken på signalen på ett rutnät som visas i följande bild:
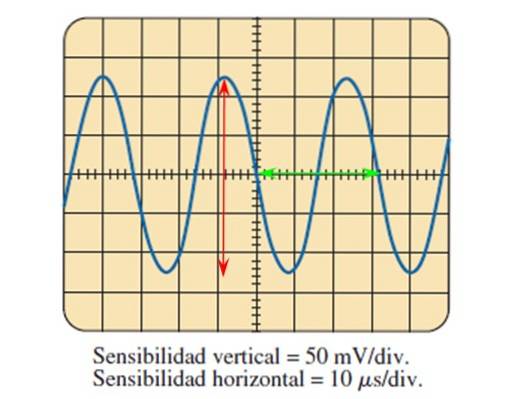
Genom bilden som tillhandahålls av oscilloskopet och känner till känslighetsjusteringen i båda axlarna är det möjligt att beräkna de vågparametrar som tidigare beskrivits..
Figuren visar den sinusformade spänningssignalen som en funktion av tiden, där varje uppdelning på den vertikala axeln är värd 50 millivolt, medan på den horisontella axeln är varje uppdelning värt 10 mikrosekunder.
Topp-till-topp-amplituden hittas genom att räkna uppdelningarna som vågen täcker vertikalt med den röda pilen:
5 divisioner räknas med hjälp av den röda pilen, så topp-toppspänningen är:
Vsid = 5 uppdelningar x 50 mV / uppdelning = 250 mV.
Toppspänning Vsid mäts från den horisontella axeln och är 125 mV.
För att hitta perioden mäts en cykel, till exempel den som avgränsas av den gröna pilen, som täcker 3,2 divisioner, då är perioden:
T = 3,2 delningar x 10 mikrosekunder / delning = 32 mikrosekunder = 32 mikrosekunder
Exempel
Exempel 1
För generatorn i fig. 3, visar från Faradays lag att den inducerade spänningen har en sinusform. Antag att slingan består av N-varv istället för bara en, alla med samma område A och roterar med konstant vinkelhastighet ω mitt i ett magnetfält B enhetlig.
Lösning
Faradays lag säger att den inducerade emf ε det är:
ε = -N (dΦB / dt)
Var ΦB är magnetfältflödet, vilket kommer att vara variabelt, eftersom det beror på hur slingan exponeras för fältet vid varje ögonblick. Det negativa tecknet beskriver helt enkelt det faktum att denna emf motsätter sig orsaken som producerar den (Lenzs lag). Flödet på grund av en enda varv är:
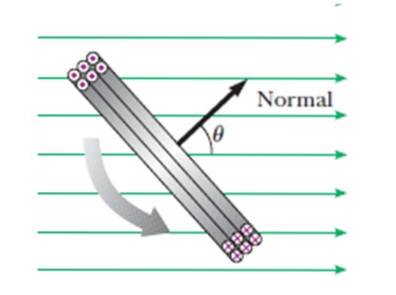
ΦB = B.A.cos θ
θ är den vinkel som vektorn är normal mot slingans plan med fältet B När rotationen fortskrider (se bild) varierar denna vinkel naturligtvis som:
θ = .t
Så att: ΦB = B.A.cos θ = B.A.cos .t. Nu behöver vi bara härleda detta uttryck med avseende på tiden och med detta får vi den inducerade emk:
ε = -N.d (B.A.cos ωt) / dt
Som fältet B är enhetligt och slingans område varierar inte, de lämnar utanför derivatet:
ε = -NBA. d (cos ωt) / dt = BANBA. sen .t
Exempel 2
En slinga har en yta på 0,100 mtvå och roterar med 60,0 varv / s, med sin rotationsaxel vinkelrät mot ett enhetligt magnetfält på 0,200 T.Vet du att spolen har 1000 varv, hitta: a) Den maximala emf som genereras, b) Spolens orientering i förhållande till magnetfältet när den inducerade maximala emf uppträder.
Lösning
a) Den maximala emf är εmax = ωNBA
Innan du fortsätter att ersätta värdena måste frekvensen 60 varv / s överföras till internationella systemenheter. Det är känt att 1 varv är lika med en varv eller 2p radianer:
60,0 varv / s = 120p radianer / s
εmax = 120p radianer x 1000 varv x 0,200 T x 0,100 mtvå = 7539,82 V = 7,5 kV
b) När detta värde inträffar sen ωt = 1 Således:
ωt = θ = 90º,
I ett sådant fall är spiralplanet parallellt med B, så att vektorn vinkelrätt mot nämnda plan bildar 90º med fältet. Detta inträffar när vektorn i svart i figur 8 är vinkelrät mot den gröna vektorn som representerar magnetfältet.
Referenser
- Boylestad, R. 2011. Introduktion till kretsanalys. 12: e. Utgåva. Pearson. 327-376.
- Figueroa, D. 2005. Elektromagnetism. Fysikserie för vetenskap och teknik. Volym 6. Redigerad av D. Figueroa. Simon Bolivar University. 115 och 244-245.
- Figueroa, D. 2006. Physics Laboratory 2. Redaktionellt Equinoccio. 03-1 och 14-1.
- Sinus vågor. Återställd från: iessierradeguara.com
- Serway, R. 2008. Fysik för vetenskap och teknik. Volym 2. Cengage Learning. 881- 884


Ingen har kommenterat den här artikeln än.