De mekanisk kraft är den hastighet med vilken arbete utförs, vilket uttrycks matematiskt med mängden arbete som utförts per tidsenhet. Och eftersom arbete utförs på bekostnad av absorberad energi kan det också anges som energi per tidsenhet.
Kallelse P till makten, W att jobba, OCH till energi och t Samtidigt kan alla ovanstående sammanfattas i lättanvända matematiska uttryck:
Nåväl:
Andra kraftenheter som används i industrier är hk (hästkraft eller hästkrafter) och CV (hästkrafter). Ursprunget till dessa enheter går också tillbaka till James Watt och den industriella revolutionen, då mätstandarden var den hastighet med vilken en häst fungerade..
Både hk och CV motsvarar ungefär ¾ kilo-W och används fortfarande i stor utsträckning, särskilt inom maskinteknik, till exempel vid beteckning av motorer.
Multiplar av watt, såsom ovannämnda kilo-W = 1000 W, används ofta också i elkraft. Detta beror på att joule är en relativt liten energienhet. Det brittiska systemet använder pund-fötter / sekund.
Artikelindex
Begreppet kraft är tillämpligt på alla typer av energi, oavsett om det är mekaniskt, elektriskt, kemiskt, vind, ljud eller av något slag. Tiden är mycket viktig i branschen, eftersom processer måste genomföras så snabbt som möjligt.
Varje motor kommer att utföra nödvändigt arbete så länge det har tillräckligt med tid, men det viktiga är att göra det på kortast möjliga tid för att öka effektiviteten..
En mycket enkel applikation beskrivs omedelbart för att klargöra skillnaden mellan arbete och makt.
Anta att ett tungt föremål dras av ett rep. För att göra detta krävs någon extern agent för att utföra nödvändigt arbete. Låt oss säga att det här agenten överför 90 J energi till objektsträngsystemet, så att det sätter igång i 10 sekunder.
I ett sådant fall är energiöverföringshastigheten 90 J / 10 s eller 9 J / s. Då kan vi bekräfta att agenten, en person eller en motor, har en uteffekt på 9 W.
Om ett annat externt medel kan uppnå samma förskjutning, antingen på kortare tid eller genom att överföra mindre mängd energi, kan den utveckla större kraft..
Ett annat exempel: antag en energiöverföring på 90 J, som lyckas sätta systemet i rörelse i 4 sekunder. Uteffekten blir 22,5W.
Kraft är nära relaterad till prestanda. Den energi som levereras till en maskin förvandlas aldrig helt till användbart arbete. En viktig del sprids vanligtvis i värme, vilket beror på många faktorer, till exempel maskinens design.
Det är därför det är viktigt att känna till maskinernas prestanda, som definieras som kvoten mellan det levererade arbetet och den levererade energin:
η = arbete som levereras av maskinen / levererad energi
Där det grekiska brevet η betecknar avkastningen, en dimensionslös kvantitet som alltid är mindre än 1. Om den också multipliceras med 100 har vi avkastningen i procent.
- Människor och djur utvecklar kraft under rörelse. Till exempel kräver trappsteg arbete mot tyngdkraften. Jämförelse av två personer som klättrar på en stege, den som klättrar upp alla steg först, har utvecklat mer kraft än den andra, men båda gjorde samma jobb.
- Hushållsapparater och maskiner har sin uteffekt specificerad. En glödlampa som är lämplig för att tända en rumsbrunn har en effekt på 100 W. Detta innebär att lampan omvandlar elektrisk energi till ljus och värme (det mesta) med en hastighet av 100 J / s.
- En gräsklippares motor kan förbruka cirka 250 W och en bils motor är i storleksordningen 70 kW.
- En hemlagad vattenpump levererar vanligtvis 0,5 hk.
- Solen genererar 3,6 x 10 26 Kraft W.
Omedelbar kraft erhålls genom att ta en oändlig tid: P = dW / dt. Kraften som producerar arbetet som orsakar den lilla oändliga förskjutningen dx det är F (båda är vektorer), därför dW = F ● dx. Att ersätta makten i allt i uttrycket, det återstår:
Människor kan generera effekt på cirka 1500 W eller 2 hästkrafter, åtminstone under en kort tid, som att lyfta vikter.
I genomsnitt är den dagliga effekten (8 timmar) 0,1 hk per person. Mycket av detta översätts till värme, ungefär samma mängd som genereras av en 75W glödlampa.
En idrottsman i träning kan generera i genomsnitt 0,5 hk motsvarande cirka 350 J / s genom att omvandla kemisk energi (glukos och fett) till mekanisk energi.
När det gäller mänsklig kraft föredras det i allmänhet att mäta i kilokalorier / timme snarare än watt. Den nödvändiga ekvivalensen är:
1 kilokalori = 1 näringskalori = 4186 J
En effekt på 0,5 hk låter som en mycket liten mängd, och det är för många applikationer.
Men 1979 skapades en människodriven cykel som kunde flyga. Paul MacCready designade Gossamer Albatross, som korsade Engelska kanalen och genererade 190 W i genomsnittlig effekt (figur 1).
En viktig applikation är fördelningen av elektrisk energi mellan användarna. De företag som levererar elräkningen för den förbrukade energin, inte den hastighet med vilken den förbrukas. Det är därför de som läser din räkning noggrant kommer att hitta en mycket specifik enhet: kilowattimme eller kW-h..
Men när Watt-namnet ingår i den här enheten avser det energi och inte kraft..
Kilowattimmarna används för att indikera förbrukningen av elektrisk energi, eftersom joule, som nämnts tidigare, är en ganska liten enhet: 1 wattimme eller W-h är arbetet på 1 timme med en effekt på 1 watt.
Därför 1 kW-h är det arbete som utförs på en timme med en effekt på 1 kW eller 1000 W. Låt oss sätta siffrorna för att konvertera dessa belopp till joule:
1 W-h = 1 W x 3600 s = 3600 J
1 kW-h = 1000 W x 3600 s = 3,6 x 10 6 J
Det beräknas att ett hushåll kan förbruka cirka 200 kW-timmar per månad.
En jordbrukare använder en traktor för att dra en bal med hö på M = 150 kg över ett 15 ° lutande plan och bära den till ladan med en konstant hastighet på 5,0 km / h. Koefficienten för kinetisk friktion mellan höbalen och rännan är 0,45. Hitta traktorns effekt.
För detta problem är det nödvändigt att rita ett frikroppsdiagram för höbal som stiger i lutningen. Vara F den kraft som appliceras av traktorn för att höja balen, α = 15º är lutningsvinkeln.
Dessutom är den kinetiska friktionskraften inblandad FRör som motsätter sig rörelse, plus det normala N och vikten W (förväxla inte viktens vikt med arbetets).
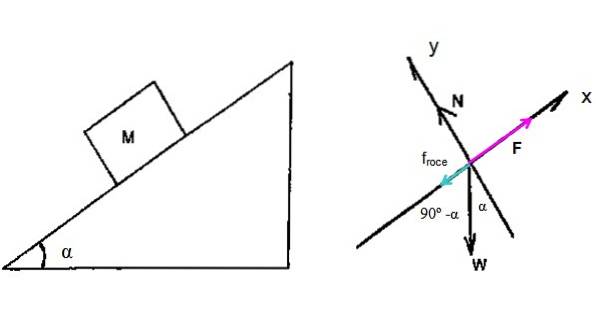
Newtons andra lag erbjuder följande ekvationer:
∑ Fx = F -Wx -FRör = 0 (eftersom balen stiger med konstant hastighet)
∑Fy = N - WY = 0 (det finns ingen rörelse längs x-axeln)
Den kinetiska friktionskraften beräknas av:
FRör = koefficient för kinetisk friktion x normalstorlek
FRör = 0,45. Wy = 0,45 x 150 kg x9,8 m / s2 x cos 15º = 639 N
F = Wx + FRör = M.g. sin α = 150 kg. 9,8 m / stvå . sin 15º + 639 N = 1019,42 N
Hastighet och kraft har samma riktning och känsla, därför:
P = F ● v = F. v
Det krävs att transformera hastighetsenheterna:
v = 5,0 km / h = 1,39 m / s
Att ersätta värden, äntligen får vi:
P = 1019,42 N x 1,39 m / s = 1417 W = 1,4 kW
Motorn som visas i figuren lyfter 2 kg-blocket, från vila, med en acceleration på 2 m / stvå och på 2 sekunder.
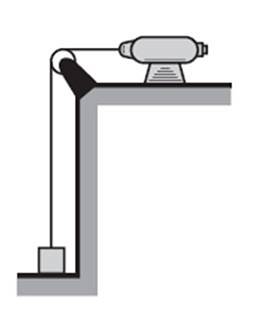
Beräkna:
a) Höjden som blocket nådde under den tiden.
b) Kraften som motorn måste utveckla för att uppnå detta.
a) Det är en jämnt varierad raklinjig rörelse, därför kommer motsvarande ekvationer att användas, med initialhastighet 0. Den uppnådda höjden ges av:
y = ½ vidtvå = ½. 2 m / stvå . (2 s)två = 4 m.
b) För att hitta den effekt som utvecklats av motorn kan ekvationen användas:
P = AW / Δt
Och eftersom kraften som utövas på blocket är genom spänningen i strängen, som är konstant i storlek:
P = (ma) .y / Δt = 2 kg x 2 m / stvå x 4 m / 2 s = 8 W.
Ingen har kommenterat den här artikeln än.