
Cross Product Properties, applikationer och övningar
De korsprodukt eller vektorprodukt det är ett sätt att multiplicera två eller flera vektorer. Det finns tre sätt att multiplicera vektorer, men inget av dessa är multiplikation i ordets vanliga mening. En av dessa former är känd som en vektorprodukt, vilket ger oss som ett resultat en tredje vektor.
Korsprodukten, som också kallas korsprodukten eller ytterprodukten, har olika algebraiska och geometriska egenskaper. Dessa egenskaper är mycket användbara, särskilt i fysikstudier..

Artikelindex
- 1 Definition
- 2 fastigheter
- 2.1 Fastighet 1
- 2.2 Fastighet 2
- 2.3 Fastighet 3
- 2.4 Fastighet 4 (produkt med tre punkter)
- 2.5 Fastighet 5 (trippel vektorprodukt)
- 2.6 Fastighet 6
- 2.7 Fastighet 7
- 2.8 Fastighet 8
- 3 applikationer
- 3.1 Beräkning av volymen för en parallellpiped
- 4 Lösta övningar
- 4.1 Övning 1
- 4.2 Övning 2
- 5 Referenser
Definition
En formell definition av vektorprodukten är följande: om A = (a1, a2, a3) och B = (b1, b2, b3) är vektorer, så är vektorprodukten av A och B, som vi kommer att beteckna som AxB, är:
AxB = (a2b3 - a3b2, a3b1 - a1b3, a1b2 - a2b1)
På grund av AxB-notationen läses den som "A cross B".
Ett exempel på hur man använder den yttre produkten är att om A = (1, 2, 3) och B = (3, -2, 4) är vektorer, så använder vi definitionen av en vektorprodukt:
AxB = (1, 2, 3) x (3, -2, 4) = (2 * 4 - 3 * (- 2), 3 * 3 - 1 * 4, 1 * (- 2) - 2 * 3)
AxB = (8 + 6, 9 - 4, - 2 - 6) = (14, 5, - 8).
Ett annat sätt att uttrycka vektorprodukten ges genom beteckningen av determinanter.
Beräkningen av en andra ordningsdeterminant ges av:
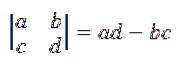
Därför kan formeln för tvärprodukten som ges i definitionen skrivas om enligt följande:
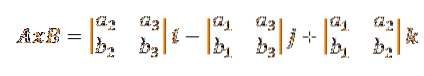
Detta förenklas vanligtvis till en tredje ordens determinant enligt följande:
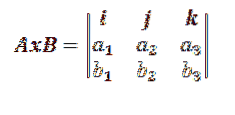
Där i, j, k representerar vektorerna som utgör grunden för R3.
Med detta sätt att uttrycka korsprodukten har vi att föregående exempel kan skrivas om som:
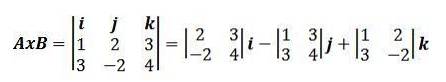
Egenskaper
Några egenskaper som vektorprodukten har är följande:
Fastighet 1
Om A är någon vektor i R3, vi måste:
- AxA = 0
- Ax0 = 0
- 0xA = 0
Dessa egenskaper är enkla att kontrollera med bara definitionen. Om A = (a1, a2, a3) har vi:
AxA = (a2a3 - a3a2, a3a1 - a1a3, a1a2 - a2a1) = (0, 0, 0) = 0.
Ax0 = (a2 * 0 - a3 * 0, a3 * 0 - a1 * 0, a1 * 0 - a2 * 0) = (0, 0, 0) = 0.
Om i, j, k representerar enhetsbasen för R3, vi kan skriva dem enligt följande:
i = (1, 0, 0)
j = (0, 1, 0)
k = (0, 0, 1)
Så vi har att följande egenskaper är sanna:
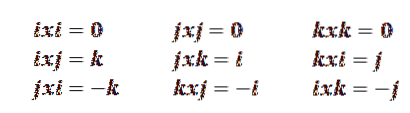
Som en minnesregel används följande cirkel ofta för att komma ihåg dessa egenskaper:
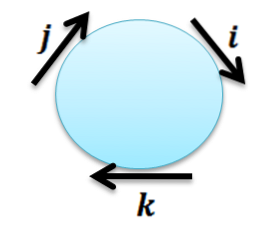
Där måste vi notera att varje vektor med sig själv ger vektor 0 som ett resultat, och resten av produkterna kan erhållas med följande regel:
Tvärprodukten av två på varandra följande vektorer i medurs riktning ger nästa vektor; och när moturs beaktas är resultatet följande vektor med negativt tecken.
Tack vare dessa egenskaper kan vi se att vektorprodukten inte är kommutativ; Observera till exempel att i x j ≠ j x i. Följande egenskap berättar hur AxB och BxA är relaterade i allmänhet.
Fastighet 2
Om A och B är vektorer av R3, vi måste:
AxB = - (BxA).
Demonstration
Om A = (a1, a2, a3) och B = (b1, b2, b3) har vi per definition en extern produkt:
AxB = (a2b3 - a3b2, a3b1 - a1b3, a1b2 - a2b1)
= (- 1) (a3b2 - a2b3, a1b3 - a3b1, a2b1 - a1b2)
= (- 1) (BxA).
Vi kan också se att den här produkten inte associerar med följande exempel:
ix (ixj) = ixk = - j men (ixi) xj = 0xj = 0
Av detta kan vi se att:
ix (ixj) ≠ (ixi) xj
Fastighet 3
Om A, B, C är vektorer av R3 och r är ett verkligt tal, följande är sant:
- Ax (B + C) = AxB + AxC
- r (AxB) = (rA) xB = Ax (rB)
Tack vare dessa egenskaper kan vi beräkna vektorprodukten med hjälp av algebra, förutsatt att beställningen respekteras. Till exempel:
Om A = (1, 2, 3) och B = (3, -2, 4) kan vi skriva om dem baserat på den kanoniska grunden för R3.
Således är A = i + 2j + 3k och B = 3i - 2j + 4k. Använd sedan tidigare egenskaper:
AxB = (i + 2j + 3k) x (3i - 2j + 4k)
= 3 (ixi) - 2 (ixj) + 4 (ixk) + 6 (jxi) - 4 (jxj) + 8 (jxk) + 9 (kxi) - 6 (kxj) +12 (kxk)
= 3 (0) - 2 (k) + 4 (- j) + 6 (- k) - 4 (0) + 8 (i) + 9 (j) - 6 (- i) +12 (0)
= - 2k - 4j - 6k + 8i + 9j + 6i = 14i + 5j - 4k
= (14, 5, - 8).
Fastighet 4 (produkt med tre punkter)
Som vi nämnde i början finns det andra sätt att multiplicera vektorer förutom vektorprodukten. Ett av dessa sätt är den skalära produkten eller den inre produkten, som betecknas A ∙ B och vars definition är:
Om A = (a1, a2, a3) och B = (b1, b2, b3), då A ∙ B = a1b1 + a2b2 + a3b3
Egenskapen som relaterar båda produkterna kallas trippel skalarprodukt.
Om A, B och C är vektorer av R3, sedan A ∙ BxC = AxB ∙ C
Som ett exempel, låt oss se att, med tanke på A = (1, 1, - 2), B = (- 3, 4, 2) och C = (- 5, 1, - 4), den här egenskapen uppfylls.
BxC = - 3k - 12j + 20k - 16i - 10j - 2i = - 18i - 22j + 17k
A ∙ BxC = (1, 1, - 2) ∙ (- 18, - 22, 17) = (1) (- 18) + (1) (- 22) + (- 2) (17) = - 74
Å andra sidan:
AxB = 4k - 2j + 3k + 2i + 6j + 8i = 10i + 4j + 7k
AxB ∙ C = (10, 4, 7) ∙ (- 5, 1, - 4) = (10) (- 5) + (4) (1) + (7) (- 4) = - 74
En annan trippelprodukt är Ax (BxC), som kallas trippelvektorprodukten..
Fastighet 5 (trippel vektorprodukt)
Om A, B och C är vektorer av R3, sedan:
Ax (BxC) = (A ∙ C) B - (A ∙ B) C
Som ett exempel, låt oss se att, givet A = (1, 1, - 2), B = (- 3, 4, 2) och C = (- 5, 1, - 4), den här egenskapen är uppfylld.
Från det föregående exemplet vet vi att BxC = (- 18, - 22, 17). Låt oss beräkna Ax (BxC):
Ax (BxC) = - 22k - 17j + 18k + 17i + 36j - 44i = - 27i + 19j - 4k
Å andra sidan måste vi:
A ∙ C = (1, 1, - 2) ∙ (- 5, 1, - 4) = (1) (- 5) + (1) (1) + (- 2) (- 4) = - 5 + 1 + 8 = 4
A ∙ B = (1, 1, - 2) ∙ (- 3, 4, 2) = (1) (- 3) + (1) (4) + (- 2) (2) = - 3 + 4 - 4 = - 3
Således måste vi:
(A ∙ C) B - (A ∙ B) C = 4 (- 3, 4, 2) + 3 (- 5, 1, - 4) = (- 12, 16, 8) + (- 15, 3, - 12) = (- 27,19, -4)
Fastighet 6
Det är en av vektorernas geometriska egenskaper. Om A och B är två vektorer i R3 och ϴ är vinkeln som bildas mellan dessa, då:
|| AxB || = || A |||| B || sin (ϴ), där || ∙ || betecknar en vektors modul eller storlek.
Den geometriska tolkningen av denna egenskap är som följer:
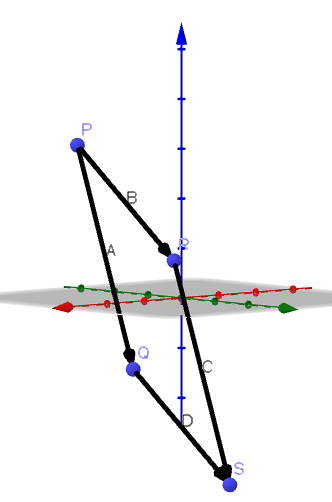
Låt A = PR och B = PQ. Därefter är vinkeln som bildas av vektorerna A och B vinkeln P för triangeln RQP, som visas i följande figur.
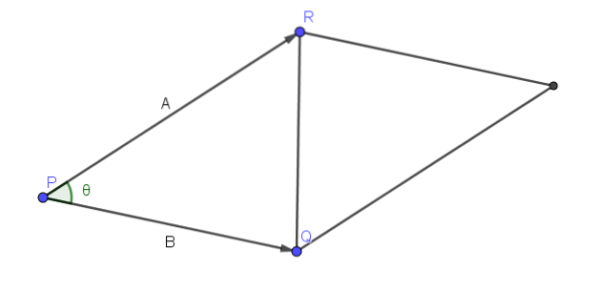
Därför är arealet av parallellogrammet som har PR och PQ som intilliggande sidor || A |||| B || sin (ϴ), eftersom vi kan ta utgångspunkt || A || och dess höjd ges av || B || sin (ϴ).
Med detta kan vi dra slutsatsen att || AxB || är området för nämnda parallellogram.
Exempel
Med tanke på följande hörn av en fyrsidig P (1, -2,3), Q (4, 3, -1), R (2, 2,1) och S (5,7, -3), visar att nämnda fyrsidiga är ett parallellogram och hitta dess område.
För detta bestämmer vi först de vektorer som bestämmer riktningen på sidorna av fyrsidan. Detta är:
A = PQ = (1 - 4, 3 + 2, - 1 - 3) = (3, 5, - 4)
B = PR = (2 - 1, 2 + 2, 1 - 3) = (1, 4, - 2)
C = RS = (5 - 2, 7 - 2, - 3 - 1) = (3, 5, - 4)
D = QS = (5 - 4, 7 - 3, - 3 + 1) = (1, 4, - 2)
Som vi kan se har A och C samma direktörvektor, så vi har att båda är parallella; detsamma händer med B och D. Därför drar vi slutsatsen att PQRS är ett parallellogram.
För att få arean för detta parallellogram beräknar vi BxA:
BxA = (i + 4j - 2k) x (3i + 5j - 4k)
= 5k + 4j - 12k - 16i - 6j + 10i
= - 6i - 2j - 7k.
Därför kommer området kvadrat att vara:
|| BxA ||två = (- 6)två + (- två)två + (- 7)två = 36 + 4 + 49 = 89.
Man kan dra slutsatsen att parallellogramområdet blir kvadratroten på 89.
Fastighet 7
Två vektorer A och B är parallella i R3 om och endast om AxB = 0
Demonstration
Det är uppenbart att om A eller B är nollvektorn uppfylls att AxB = 0. Eftersom nollvektorn är parallell med någon annan vektor är egenskapen giltig.
Om ingen av de två vektorerna är nollvektorn har vi att deras storlek skiljer sig från noll; det vill säga båda || A || ≠ 0 som || B || ≠ 0, så vi kommer att ha || AxB || = 0 om och endast om sin (ϴ) = 0, och detta händer om och endast om ϴ = π eller ϴ = 0.
Därför kan vi dra slutsatsen att AxB = 0 om och bara om ϴ = π eller ϴ = 0, vilket bara händer när båda vektorerna är parallella med varandra.
Fastighet 8
Om A och B är två vektorer i R3, då är AxB vinkelrätt mot både A och B.
Demonstration
För detta bevis, låt oss komma ihåg att två vektorer är vinkelräta om A ∙ B är lika med noll. Dessutom vet vi att:
A ∙ AxB = AxA ∙ B, men AxA är lika med 0. Därför har vi:
A ∙ AxB = 0 ∙ B = 0.
Genom detta kan vi dra slutsatsen att A och AxB är vinkelräta mot varandra. På samma sätt måste vi:
AxB ∙ B = A ∙ BxB.
Eftersom BxB = 0 har vi:
AxB ∙ B = A ∙ 0 = 0.
Därför är AxB och B vinkelräta mot varandra och med detta demonstreras egenskapen. Detta är mycket användbart eftersom det låter oss bestämma ekvationen för ett plan.
Exempel 1
Skaffa en ekvation av planet som passerar genom punkterna P (1, 3, 2), Q (3, - 2, 2) och R (2, 1, 3).
Låt A = QR = (2 - 3.1 + 2, 3 - 2) och B = PR = (2 - 1.1 - 3, 3 - 2). Då är A = - i + 3j + k och B = i - 2j + k. För att hitta planet som bildas av dessa tre punkter räcker det att hitta en vektor som är normal för planet, vilket är AxB.
AxB = (- i + 3j + k) x (i - 2j + k) = 5i + 2j - k.
Med denna vektor och tar punkten P (1, 3, 2) kan vi bestämma planens ekvation enligt följande:
(5, 2, - 1) ∙ (x - 1, y - 3, z - 2) = 5 (x - 1) + 2 (y - 3) - (z - 2) = 0
Således har vi att ekvationen för planet är 5x + 2y - z - 9 = 0.
Exempel 2
Hitta ekvationen för planet som innehåller punkten P (4, 0, - 2) och som är vinkelrät mot vart och ett av planen x - y + z = 0 och 2x + y - 4z - 5 = 0 .
Att veta att en normal vektor till en plan ax + med + cz + d = 0 är (a, b, c), har vi att (1, -1,1) är en normal vektor av x - y + z = 0 y (2,1, - 4) är en normalvektor av 2x + y - 4z - 5 = 0.
Därför måste en normal vektor till det sökta planet vara vinkelrät mot (1, -1,1) och till (2, 1, - 4). Nämnda vektor är:
(1, -1,1) x (2,1, - 4) = 3i + 6j + 3k.
Sedan har vi att det sökta planet är det som innehåller punkten P (4,0, - 2) och har vektorn (3,6,3) som en normal vektor.
3 (x - 4) + 6 (y - 0) + 3 (z + 2) = 0
x + 2y + z - 2 = 0.
Applikationer
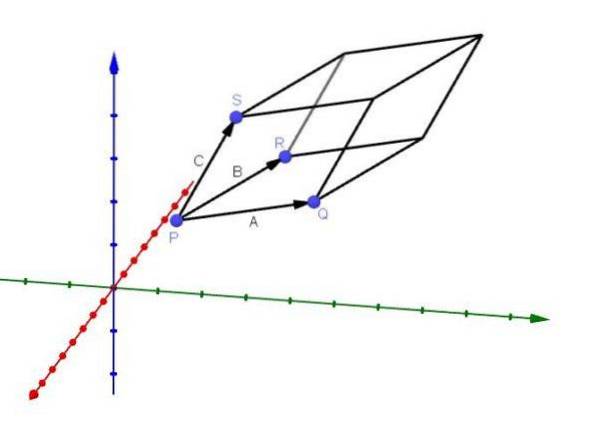
Beräkning av volym för en parallellpiped
En applikation som har den tredubbla skalära produkten är att kunna beräkna volymen för en parallellpipad vars kanter ges av vektorerna A, B och C, som visas i figuren:
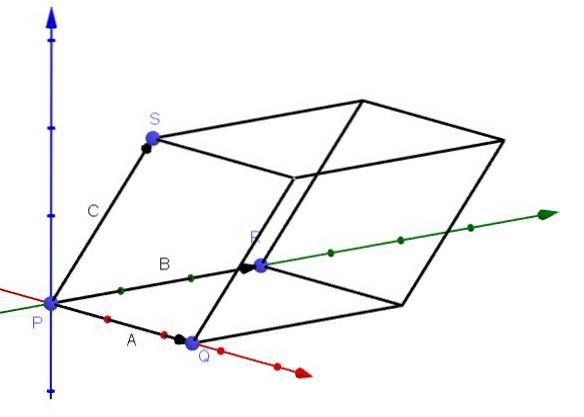
Vi kan härleda denna applikation på följande sätt: som vi sa tidigare är vektorn AxB en vektor som är normal för planet A och B. Vi har också att vektorn - (AxB) är en annan vektor som är normal för planet.
Vi väljer den normala vektorn som bildar den minsta vinkeln med vektorn C; utan förlust av generalitet, låt AxB vara vektorn vars vinkel med C är minsta.
Vi har att både AxB och C har samma utgångspunkt. Vidare vet vi att arean av parallellogrammet som utgör basen för parallellpiped är || AxB ||. Därför, om höjden på parallelepiped ges av h, har vi att dess volym kommer att vara:
V = || AxB || h.
Å andra sidan, låt oss överväga den skalära produkten mellan AxB och C, som kan beskrivas enligt följande:
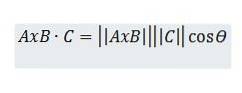
Men genom trigonometriska egenskaper har vi det h = || C || cos (ϴ), så vi har:
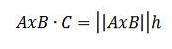
På detta sätt har vi det:
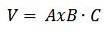
I allmänna termer har vi att volymen för en parallellpipad ges av det absoluta värdet för den trippel skalära produkten AxB ∙ C.
Lösta övningar
Övning 1
Med tanke på punkterna P = (5, 4, 5), Q = (4, 10, 6), R = (1, 8, 7) och S = (2, 6, 9), bildar dessa punkter en parallellpiped vars kanter de är PQ, PR och PS. Bestäm volymen för parallellpiped.
Lösning
Om vi tar:
- A = PQ = (-1, 6, 1)
- B = PR = (-4, 4, 2)
- C = PS = (-3, 2, 2)
Med hjälp av egenskapen för den tredubbla skalära produkten har vi:
AxB = (-1, 6, 1) x (-4, 4, 2) = (8, -2, 20).
AxB ∙ C = (8, -2, 20) ∙ (-3, 2, 2) = -24 -4 +80 = 52.
Därför har vi att volymen för nämnda parallellpiped är 52.
Övning 2
Bestäm volymen för en parallellpipad vars kanter ges av A = PQ, B = PR och C = PS, där punkterna P, Q, R och S är (1, 3, 4), (3, 5, 3), (2, 1, 6) respektive (2, 2, 5).
Lösning
Först har vi att A = (2, 2, -1), B = (1, -2, 2), C = (1, -1, 1).
Vi beräknar AxB = (2, 2, -1) x (1, -2, 2) = (2, -5, -6).
Sedan beräknar vi AxB ∙ C:
AxB ∙ C = (2, -5, -6) ∙ (1, -1, 1) = 2 + 5 - 6 = 1.
Således drar vi slutsatsen att volymen för nämnda parallellpiped är 1 kubik enhet.
Referenser
- Leithold, L. (1992). Beräkningen med analytisk geometri. HARLA, S.A.
- Resnick, R., Halliday, D., & Krane, K. (2001). Fysik Vol. 1. Mexiko: Kontinentalt.
- Saenz, J. (s.f.). Vector Calculus 1ed. Hypotenusa.
- Spiegel, M. R. (2011). Vektoriell analys 2ed. Mc Graw Hill.
- Zill, D. G., & Wright, W. (2011). Beräkning av flera variabler 4ed. Mc Graw Hill.



Ingen har kommenterat den här artikeln än.