De spänningsdelare eller spänningsdelare består av en sammanslutning av motstånd eller impedanser i serie kopplade till en källa. På detta sätt spänningen V levereras av källan - ingångsspänning - fördelas proportionellt i varje element, enligt Ohms lag:
Vi = I.Zi.
Där Vi är spänningen över kretselementet, jag är strömmen som strömmar genom den och Zi motsvarande impedans.
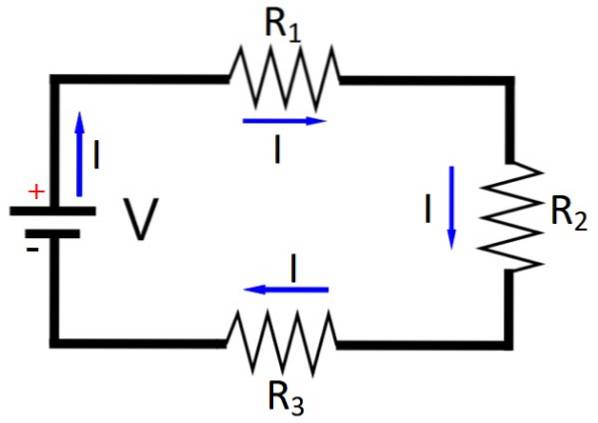
När källan och elementen ordnas i en sluten krets måste Kirchhoffs andra lag uppfyllas, som säger att summan av all spänning sjunker och stiger är lika med 0.
Till exempel, om kretsen som ska betraktas är rent resistiv och en 12-volts källa är tillgänglig, helt enkelt genom att placera två identiska motstånd i serie med nämnda källa, kommer spänningen att delas: varje motstånd kommer att ha 6 volt. Och med tre identiska motstånd erhålls 4 V i var och en.
Eftersom källan representerar en spänningsökning, är V = +12 V. Och i varje motstånd finns spänningsfall som representeras av negativa tecken: - 6 V respektive - 6 V. Det är lätt att se att Kirchoffs andra lag är uppfylld:
+12 V - 6 V - 6 V = 0 V
Det är här namnet på spänningsdelaren kommer ifrån, eftersom genom seriemotstånd kan lägre spänningar lätt erhållas från en källa med högre spänning.
Artikelindex
Låt oss fortsätta överväga en ren resistiv krets. Vi vet att strömmen I som går igenom en krets av motstånd i serie kopplad till en källa som visas i figur 1 är densamma. Och enligt Ohms lag och Kirchoffs andra lag:
V = IR1 + ATT GÅtvå + ATT GÅ3 +... ATT GÅi
Där R1, Rtvå... Ri representerar varje seriemotstånd i kretsen. Därför:
V = I ∑ Ri
Så strömmen visar sig vara:
I = V / ∑ Ri
Låt oss nu beräkna spänningen över ett av motstånden, motståndet Ri till exempel:
Vi = (V / ∑ Ri) Ri
Den föregående ekvationen skrivs om enligt följande och vi har spänningsdelningsregeln redo för ett batteri och N-motstånd i serie:
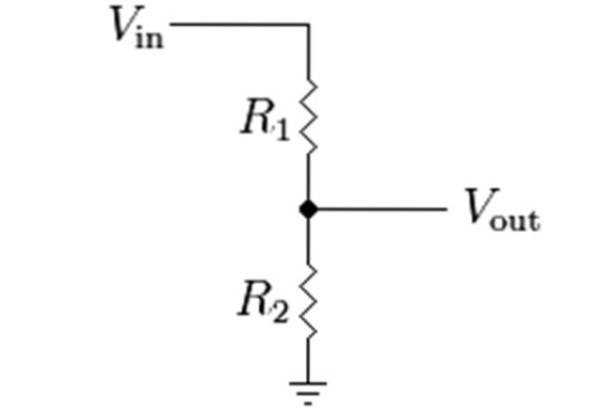
Om vi har en spänningsdelarkrets med två motstånd blir ekvationen ovan:
Och i det speciella fallet där R1 = Rtvå, Vi = V / 2, oavsett ström, som anges i början. Detta är den enklaste spänningsdelaren av alla.
I följande figur är diagrammet för denna avdelare, där V, ingångsspänningen, symboliseras som Vi, och Vi är spänningen som erhålls genom att dela spänningen mellan motstånden R1 och Rtvå.
Spänningsdelarregeln kommer att tillämpas i två resistiva kretsar för att erhålla lägre spänningar.
En 12 V-källa finns tillgänglig, som måste delas upp i 7 V och 5 V med hjälp av två motstånd R1 och Rtvå. Det finns ett 100 Ω fast motstånd och ett variabelt motstånd vars intervall är mellan 0 och 1 kΩ. Vilka alternativ finns för att konfigurera kretsen och ställa in värdet på motståndet Rtvå?
För att lösa denna övning används spänningsdelarens regel för två motstånd:
Antag att R1 är motståndet som finns vid en spänning på 7 V och där placeras det fasta motståndet R1 = 100 Ω
Det okända motståndet Rtvå måste vara vid 5 V:
Och R1 vid 7 V:
5 (R.två +100) = 12 Rtvå
500 = 7 Rtvå
Rtvå = 71,43 Ω
På samma sätt kan du använda den andra ekvationen för att erhålla samma värde eller ersätta det erhållna resultatet för att kontrollera jämlikhet.
Om nu det fasta motståndet placeras som Rtvå, då blir det R1 är vid 7 V:
5 (100 + R1) = 100 x 12
500 + 5R1 = 1200
R1 = 140 Ω
På samma sätt är det möjligt att verifiera att detta värde uppfyller den andra ekvationen. Båda värdena ligger inom det variabla motståndsområdet, därför är det möjligt att implementera den begärda kretsen på båda sätten.
En likström voltmeter för att mäta spänningar inom ett visst område, är baserad på spänningsdelaren. För att bygga en sådan voltmeter krävs en galvanometer, till exempel D'Arsonval.
Det är en mätare som detekterar elektriska strömmar, utrustad med en graderad skala och en indikationsnål. Det finns många galvanometrormodeller, den i figuren är mycket enkel, med två anslutningsterminaler på baksidan..
Galvanometern har ett inre motstånd RG, som endast tål en liten ström, kallad maximal ström IG. Följaktligen är spänningen över galvanometern V.m = JagGRG.
För att mäta spänning placeras voltmätaren parallellt med elementet som ska mätas och dess inre motstånd måste vara tillräckligt stort för att inte dra ström från kretsen, annars kommer det att förändra det..
Om vi vill använda galvanometern som en mätare får spänningen som ska mätas inte överstiga det högsta tillåtna, vilket är den maximala avböjningen av nålen som enheten har. Men vi antar att Vm är liten, eftersom jagG och RG dom är.
Men när galvanometern är ansluten i serie med ett annat motstånd RS, ring upp begränsande motstånd, vi kan utöka mätområdet för galvanometern från den lilla V.m upp till en viss högre spänning ε. När denna spänning uppnås upplever instrumentnålen maximal avböjning.
Designschemat är som följer:
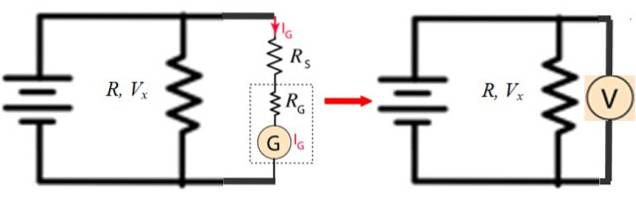
I figur 4 till vänster är G galvanometern och R är vilket motstånd du vill mäta spänningen V.x.
Bilden till höger visar hur kretsen med G, RG och RS motsvarar en voltmeter, som är placerad parallellt med motståndet R.
Antag till exempel att det inre motståndet i galvanometern är RG = 50 Ω och den maximala strömmen den stöder är IG = 1 mA beräknas begränsningsmotståndet RS för den voltmeter som byggts med denna galvanometer för att mäta en maximal spänning på 1 V enligt följande:
JagG (RS + RG) = 1 V
RS = (1 V / 1 x 10-3 A) - RG
RS = 1000 Ω - 50 Ω = 950 Ω
Ingen har kommenterat den här artikeln än.