
Vad är akustisk impedans? Applikationer och övningar
De akustisk impedans eller specifik akustisk impedans är materialets motstånd mot ljudvågornas passage. Det är konstant för ett visst medium, som går från ett stenigt lager i det inre av jorden till den biologiska vävnaden.
Betecknar den akustiska impedansen som Z, i matematisk form har vi:
Z = ρ.v
Där ρ är mediets densitet och v ljudets hastighet. Detta uttryck gäller för en plan våg som rör sig i en vätska.
I SI International System-enheter är densiteten i kg / m3 och hastigheten i m / s. Därför är enheterna med akustisk impedans kg / mtvå.s.
På samma sätt definieras den akustiska impedansen som kvoten mellan trycket p och hastigheten:
Z = p / v
Uttryckt på detta sätt är Z analogt med det elektriska motståndet R = V / I, där trycket spelar rollen som spänning och hastighet som för ström. Andra SI-enheter av Z skulle vara Pa.s / m eller N.s / m3, helt likvärdiga med de tidigare angivna.
Artikelindex
- 1 Överföring och reflektion av ljudvågen
- 1.1 Överförings- och reflektionskoefficienter
- 2 Applikationer och övningar
- 2.1 - Övning löst 1
- 2.2 - Övning löst 2
- 3 Referenser
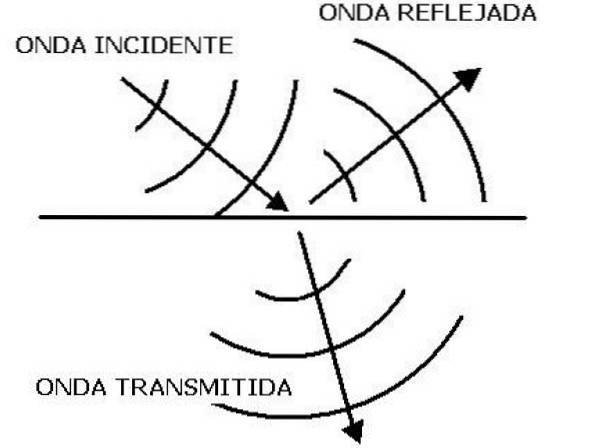
Ljudvågsöverföring och reflektion
När du har två medel för olika impedanser Z1 och Ztvå, en del av en ljudvåg som träffar gränssnittet för båda kan överföras och en annan del kan reflekteras. Denna reflekterade våg, eller ekot, är den som innehåller viktig information om det andra mediet..
Det sätt på vilket energin som transporteras av vågen fördelas beror på reflektionskoefficienterna R och transmissionskoefficienten T, två mycket användbara kvantiteter för att studera ljudvågens förökning. För reflektionskoefficienten är det kvoten:
R = Ir / Jageller
Där jageller är intensiteten i den infallande vågen och jagr är den reflekterade vågens intensitet. På samma sätt har vi överföringskoefficienten:
T = jagt / Jageller
Nu kan det visas att intensiteten hos en planvåg är proportionell mot dess amplitud A:
I = (1/2) Z.ωtvå .TILLtvå
Där Z är den akustiska impedansen för mediet och ω är frekvensen för vågen. Å andra sidan är kvoten mellan den sända amplituden och den infallande amplituden:
TILLt/TILLeller = 2Z1/ (Z1 +Ztvå)
Vilket tillåter kvoten It / Jageller uttrycks i termer av amplituden av incidenten och överförda vågor som:
Jagt / Jageller = ZtvåTILLttvå / Z1TILLellertvå
Med hjälp av dessa uttryck erhålls R och T i termer av den akustiska impedansen Z.
Överförings- och reflektionskoefficienter
Ovanstående kvot är exakt överföringskoefficienten:
T = (Ztvå/ Z1) [2.Z1/ (Z1 +Ztvå)]två = 4Z1Ztvå / (Z1 +Ztvå)två
Eftersom inga förluster övervägs är det sant att incidentintensiteten är summan av den överförda intensiteten och den reflekterade intensiteten:
Jageller = Jagr + Jagt → (Ir / Jageller) + (Jagt / Jageller) = 1
Detta gör att vi kan hitta ett uttryck för reflektionskoefficienten när det gäller impedanserna för de två medierna:
R + T = 1 → R = 1 - T
Genomförande av en liten algebra för att ordna om termerna är reflektionskoefficienten:
R = 1 - 4Z1Ztvå / (Z1 +Ztvå)två = (Z1 - Ztvå)två/ (Z1 +Ztvå)två
Och eftersom informationen relaterad till det andra mediet finns i den reflekterade pulsen är reflektionskoefficienten av stort intresse..
Således, när de två medierna har en stor skillnad i impedans, blir täljaren för det föregående uttrycket större. Då är den reflekterade vågens intensitet hög och innehåller bra information om mediet..
När det gäller den del av vågen som överförs till det andra mediet bleknar den gradvis och energin försvinner som värme..
Applikationer och övningar
Överförings- och reflektionsfenomen ger upphov till flera mycket viktiga applikationer, till exempel ekolod som utvecklats under andra världskriget och används för att upptäcka föremål. Förresten, vissa däggdjur som fladdermöss och delfiner har ett inbyggt ekolodssystem.
Dessa egenskaper används också ofta för att studera det inre av jorden i seismiska prospekteringsmetoder, vid ultraljud medicinsk avbildning, mätning av bentäthet och avbildning av olika strukturer för fel och defekter..
Akustisk impedans är också en viktig parameter när man utvärderar ljudresponsen för ett musikinstrument..
- Löst övning 1
Ultraljudstekniken för att avbilda biologisk vävnad använder högfrekventa ljudpulser. Ekona innehåller information om organ och vävnader som de passerar genom, vilket en programvara ansvarar för att översätta till en bild.
En ultraljudspuls riktad mot fett-muskelgränssnittet skärs in. Hitta de uppgifter som tillhandahålls:
a) Akustisk impedans för varje vävnad.
b) Procentandelen ultraljud reflekterad vid gränsytan mellan fett och muskler.
Fett
- Densitet: 952 kg / m3
- Ljudhastighet: 1450 m / s
Muskel
- Densitet: 1075 kg / m3
- Ljudhastighet: 1590 m / s
Lösning till
Den akustiska impedansen för varje vävnad hittas genom att ersätta i formeln:
Z = ρ.v
På det här sättet:
Zfett = 952 kg / m3 x 1450 m / s = 1,38 x 106 kg / mtvå.s
Zmuskel = 1075 kg / m3 x 1590 m / s = 1,71 x 106 kg / mtvå.s
Lösning b
För att hitta den procentuella intensiteten som reflekteras vid gränsytan mellan de två vävnaderna används reflektionskoefficienten som ges av:
R = (Z1 - Ztvå)två/ (Z1 +Ztvå)två
Här Zfett = Z1 och Zmuskel = Ztvå. Reflektionskoefficienten är en positiv kvantitet som garanteras av kvadraterna i ekvationen.
Ersätta och utvärdera:
R = (1,38 x 106 - 1,71 x 106 )två / (1,38 x 106 + 1,71 x 106 )två = 0,0114.
När vi multiplicerar med 100 kommer procenten att återspeglas: 1,14% av incidentintensiteten.
- Övning löst 2
En ljudvåg har en intensitetsnivå på 100 decibel och faller normalt på vattenytan. Bestäm intensitetsnivån för den överförda vågen och den för den reflekterade vågen.
Data:
Vatten
- Densitet: 1000 kg / m3
- Ljudhastighet: 1430 m / s
Luft
- Densitet: 1,3 kg / m3
- Ljudhastighet: 330 m / s
Lösning
Intensitetsnivån i decibel av en ljudvåg, betecknas som L, är dimensionell och ges av formeln:
L = 10 logg (I / 10-12)
Öka till 10 på båda sidor:
10 L / 10 = I / 10-12
Eftersom L = 100 resulterar det i:
I / 10-12 = 1010
Enhetsintensiteter ges i termer av effekt per ytenhet. I det internationella systemet är de Watt / mtvå. Därför är intensiteten i den infallande vågen:
Jageller = 1010 . 10-12 = 0,01 W / mtvå.
För att hitta intensiteten för den sända vågen beräknas transmissionskoefficienten och multipliceras sedan med incidentintensiteten.
De respektive impedanserna är:
ZVatten = 1000 kg / m3 x 1430 m / s = 1,43 x 106 kg / mtvå.s
Zluft = 1,3 kg / m3 x 330 m / s = 429 kg / mtvå.s
Ersätta och utvärdera i:
T = 4Z1Ztvå / (Z1 +Ztvå)två = 4 × 1,43 x 106 x 429 / (1,43 x 106 + 429)två = 1,12 x 10-3
Så intensiteten hos den sända vågen är:
Jagt = 1,12 x 10-3 x 0,01 W / mtvå = 1,12 x 10-5 W / mtvå
Dess intensitetsnivå i decibel beräknas av:
Lt = 10 logg (It / 10-12) = 10 logg (1,12 x 10-5 / 10-12) = 70,3 dB
För sin del är reflektionskoefficienten:
R = 1 - T = 0,99888
Med detta är intensiteten hos den reflekterade vågen:
Jagr = 0,99888 x 0,01 W / mtvå = 9,99 x 10-3 W / mtvå
Och dess intensitetsnivå är:
Lt = 10 logg (Ir / 10-12) = 10 logg (9,99 x 10-3 / 10-12) = 100 dB
Referenser
- Andriessen, M. 2003. HSC Physics Course. Jacaranda.
- Baranek, L. 1969. Akustik. Andra upplagan. Ledare Hispano Americana.
- Kinsler, L. 2000. Fundamentals of Acoustics. Wiley och söner.
- Lowrie, W. 2007. Fundamentals of Geophysics. 2: a. Utgåva. Cambridge University Press.
- Wikipedia. Akustisk impedans. Återställd från: en.wikipedia.org.



Ingen har kommenterat den här artikeln än.