De exponentiell utjämning det är ett sätt att prognostisera efterfrågan på en artikel under en viss period. Denna metod uppskattar att efterfrågan kommer att vara lika med genomsnittet av den historiska konsumtionen under en given period, vilket ger en större vikt eller vikt för de värden som ligger närmare i tiden. Dessutom, för följande prognoser ta hänsyn till det befintliga felet i den aktuella prognosen.
Efterfrågeprognosering är metoden för att projicera kundernas efterfrågan på en produkt eller tjänst. Denna process är kontinuerlig, där chefer använder historiska data för att beräkna vad de förväntar sig att försäljningsefterfrågan på en vara eller tjänst ska vara..
Information från företagets förflutna används genom att lägga till den i marknadsdata för att se om försäljningen kommer att öka eller minska.
Resultaten av efterfrågan prognosen används för att sätta mål för försäljningsavdelningen, försöker hålla sig i linje med företagets mål.
Artikelindex
Utjämning är en mycket vanlig statistisk process. Utjämnade data finns ofta i olika former av vardag. Varje gång ett medel används för att beskriva något används ett utjämnat antal.
Antag att den varmaste vintern på rekord upplevdes i år. För att kvantifiera det börjar vi med en uppsättning dagliga temperaturdata för vinterperioden för varje registrerat historiskt år..
Detta genererar ett antal nummer med stora "hopp". Du behöver ett nummer som eliminerar alla dessa hopp från data för att lättare kunna jämföra en vinter med en annan.
Att eliminera datahoppet kallas utjämning. I detta fall kan ett enkelt medelvärde användas för att uppnå utjämning.
För att prognostisera efterfrågan används också utjämning för att eliminera variationer i historisk efterfrågan. Detta möjliggör bättre identifiering av efterfrågan mönster, som kan användas för att uppskatta framtida efterfrågan..
Variationer i efterfrågan är samma koncept som "hopp" av temperaturdata. Det vanligaste sättet att ta bort variationer i efterfrågan är att använda ett genomsnitt eller specifikt ett rörligt medel..
Det rörliga genomsnittet använder ett fördefinierat antal perioder för att beräkna genomsnittet, och dessa perioder rör sig när tiden går..
Till exempel, om ett glidande genomsnitt på fyra månader används och idag är den 1 maj, kommer den genomsnittliga efterfrågan för januari, februari, mars och april att användas. Den 1 juni kommer kravet på februari, mars, april och maj att användas.
När du använder ett enkelt medelvärde tillämpas samma betydelse på varje värde i datamängden. Därför representerar varje månad 25% av det glidande genomsnittet i ett glidande genomsnitt på fyra månader..
Genom att använda efterfrågeshistoriken för att projicera framtida efterfrågan är det självklart att den senaste perioden har en större inverkan på prognosen..
Du kan anpassa beräkningen av det glidande genomsnittet för att tillämpa olika "vikter" för varje period för att uppnå önskat resultat..
Dessa vikter uttrycks i procent. Den totala vikten för alla perioder måste uppgå till 100%.
Därför kan du subtrahera 35% från 100% om du vill tillämpa 35% som vikten för den närmaste perioden i det fyra månaders vägda genomsnittet och lämna 65% för att dela mellan de tre återstående perioderna.
Till exempel kan du få en viktning på 15%, 20%, 30% respektive 35% under de fyra månaderna (15 + 20 + 30 + 35 = 100).
Kontrollingången för den exponentiella utjämningsberäkningen är känd som utjämningsfaktorn. Representerar vikten på efterfrågan för den senaste perioden.
Om 35% används som den senaste periodvikten i den vägda glidande genomsnittliga beräkningen kan du också välja att använda 35% som utjämningsfaktor i den exponentiella utjämningsberäkningen..
Skillnaden i den exponentiella utjämningsberäkningen är att istället för att behöva räkna ut hur mycket vikt som ska appliceras på varje föregående period, används utjämningsfaktorn för att göra det automatiskt..
Detta är den "exponentiella" delen. Om 35% används som utjämningsfaktor blir efterfrågan på den senaste perioden 35%. Viktningen av efterfrågan från föregående period till den senaste kommer att vara 65% av 35%.
65% kommer från att subtrahera 35% från 100%. Detta motsvarar 22,75% viktning för den perioden. Nästa efterfrågan kommer att vara 65% från 65% från 35%, vilket motsvarar 14,79%.
Den föregående perioden kommer att vägas till 65% av 65% av 65% av 35%, vilket motsvarar 9,61%. Detta kommer att göras för alla tidigare perioder, fram till den första perioden.
Formeln för beräkning av exponentiell utjämning är som följer: (D * S) + (P * (1-S)), där,
D = periodens senaste efterfrågan.
S = utjämningsfaktor, representerad i decimalform (35% skulle vara 0,35).
P = prognos för den senaste perioden, resultat av utjämningsberäkningen för föregående period.
Förutsatt att vi har en utjämningsfaktor på 0,35 skulle vi då ha: (D * 0,35) + (P * 0,65).
Som du kan se är de enda dataingångarna som krävs efterfrågan och den senaste periodprognosen..
Ett försäkringsbolag har beslutat att utvidga sin marknad till den största staden i landet och tillhandahålla försäkringar för fordon.
Som en första åtgärd vill företaget förutsäga hur mycket fordonsförsäkring som kommer att köpas av invånarna i denna stad.
För att göra detta kommer de att använda den ursprungliga informationen om hur mycket bilförsäkring som köpts i en annan mindre stad.
Prognos för efterfrågan för period 1 är 2 869 avtalade fordonsförsäkringar, men den faktiska efterfrågan under den perioden var 3 200.
Enligt företagets bedömning tilldelar det en utjämningsfaktor på 0,35. Den prognostiserade efterfrågan för följande period är: P2 = (3200 * 0,35) + 2869 * (1-0,35) = 2984,85.
Samma beräkning gjordes för hela året med följande jämförelsetabell mellan vad som faktiskt erhölls och vad som prognostiserades för den månaden.
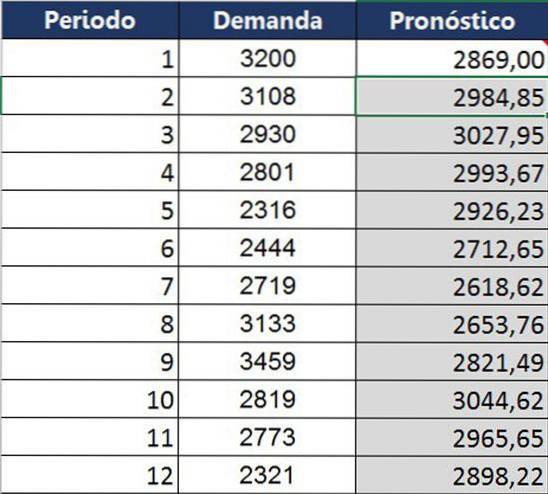
Jämfört med genomsnittliga tekniker kan exponentiell utjämning förutsäga trenden bättre. Det är dock fortfarande kort, som visas i diagrammet:
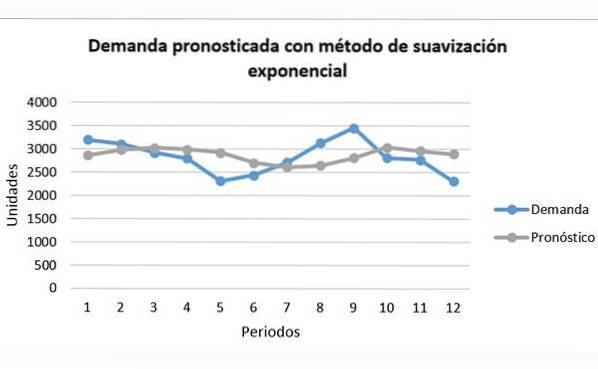
Det kan ses hur den grå linjen i prognosen kan ligga långt under eller över den blå efterfrågan utan att kunna följa den helt.
Ingen har kommenterat den här artikeln än.