
Chebyshovs sats vad det är, applikationer och exempel
De Chebyshovs sats (eller Chebyshovs ojämlikhet) är ett av de viktigaste klassiska resultaten av sannolikhetsteorin. Det gör det möjligt att uppskatta sannolikheten för en händelse som beskrivs i termer av en slumpmässig variabel X, genom att förse oss med en gräns som inte beror på fördelningen av den slumpmässiga variabeln utan på variansen av X.
Satsen är uppkallad efter den ryska matematikern Pafnuty Chebyshov (även skriven som Chebychev eller Tchebycheff) som, trots att han inte var den första som satte satsen, var den första som gav ett bevis 1867.

Denna ojämlikhet, eller de som på grund av deras egenskaper kallas Chebyshovs ojämlikhet, används främst för att approximera sannolikheter genom att beräkna gränser.
Artikelindex
- 1 Vad gör?
- 2 Tillämpningar och exempel
- 2.1 Begränsning av sannolikheter
- 2.2 Bevis på gränssatser
- 2.3 Provstorlek
- 3 Ojämlikheter av Chebyshov-typ
- 4 Referenser
Vad består det av?
I studien av sannolikhetsteori händer det att om fördelningsfunktionen hos en slumpmässig variabel X är känd, kan dess förväntade värde eller matematiska förväntan E (X) - och dess varians Var (X) beräknas, så länge sådana mängder finns . Det motsatta är dock inte nödvändigtvis sant..
Det vill säga att veta E (X) och Var (X) är det inte nödvändigtvis möjligt att erhålla fördelningsfunktionen för X, därför är kvantiteter såsom P (| X |> k) för vissa k> 0 mycket svåra att få. Men tack vare Chebyshovs ojämlikhet är det möjligt att uppskatta sannolikheten för den slumpmässiga variabeln.
Chebyshovs sats berättar att om vi har en slumpmässig variabel X över ett provutrymme S med en sannolikhetsfunktion p, och om k> 0, då:
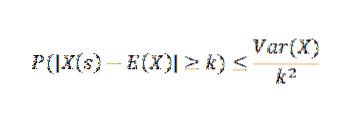
Tillämpningar och exempel
Bland de många tillämpningarna av Chebyshovs sats kan följande nämnas:
Begränsande sannolikheter
Detta är den vanligaste applikationen och används för att ge en övre gräns för P (| X-E (X) | ≥k) där k> 0, endast med variansen och förväntningen på den slumpmässiga variabeln X, utan att känna till sannolikhetsfunktionen.
Exempel 1
Antag att antalet produkter som tillverkas i ett företag under en vecka är en slumpmässig variabel med i genomsnitt 50.
Om det är känt att variansen för en produktionsvecka är lika med 25, vad kan vi säga om sannolikheten att produktionen den här veckan skiljer sig mer än 10 från medelvärdet?
Lösning
Tillämpa Chebyshovs ojämlikhet har vi:
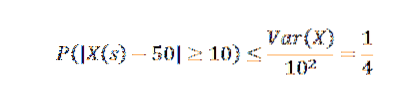
Av detta kan vi få fram att sannolikheten att antalet artiklar överstiger genomsnittet med mer än 10 under produktionsveckan är högst 1/4.
Bevis på gränssatser
Chebyshovs ojämlikhet spelar en viktig roll för att bevisa de viktigaste gränssatserna. Som ett exempel har vi följande:
Svag lag i stort antal
Denna lag fastställer att givet en sekvens X1, X2, ..., Xn, ... av oberoende slumpmässiga variabler med samma genomsnittliga fördelning E (Xi) = μ och varians Var (X) = σtvå, och ett känt medelprov av:
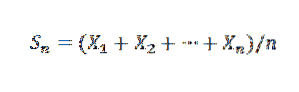
Sedan för k> 0 har vi:
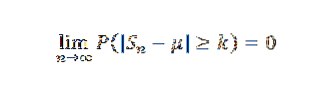
Eller motsvarande:
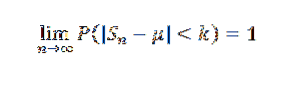
Demonstration
Låt oss först märka följande:
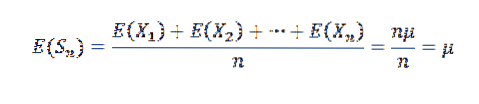
Eftersom X1, X2, ..., Xn är oberoende följer det att:
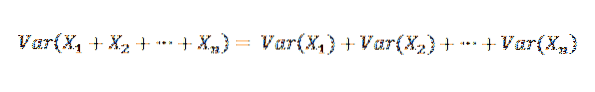
Därför är det möjligt att ange följande:
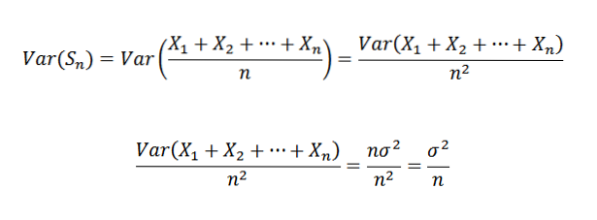
Sedan använder vi Chebyshovs teorem:
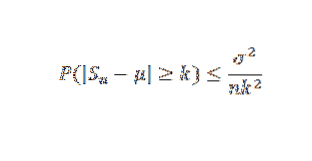
Slutligen är satsen resultatet av att gränsen till höger är noll när n tenderar att vara oändligt.
Det bör noteras att detta test endast gjordes för det fall där variansen av Xi existerar; det vill säga det skiljer sig inte. Således observerar vi att satsen alltid är sant om E (Xi) existerar.
Chebyshov begränsar satsen
Om X1, X2,…, Xn, ... är en sekvens av oberoende slumpmässiga variabler så att det finns en del C< infinito, tal que Var(Xn) ≤ C para todo n natural, entonces para cualquier k>0:
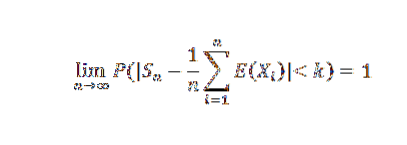
Demonstration
Eftersom varianssekvensen är enhetligt begränsad har vi den Var (Sn) ≤ C / n, för alla naturliga n. Men vi vet att:
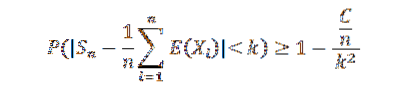
Att göra n tenderar mot oändlighet, följande resultat:
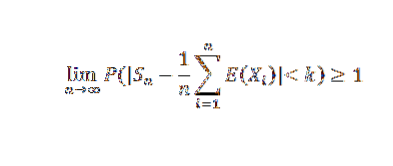
Eftersom en sannolikhet inte kan överstiga värdet 1 uppnås önskat resultat. Som en konsekvens av denna teorem kan vi nämna Bernoullis speciella fall.
Om ett experiment upprepas n gånger oberoende med två möjliga resultat (misslyckande och framgång), där p är sannolikheten för framgång i varje experiment och X är den slumpmässiga variabeln som representerar antalet erhållna framgångar, så för varje k> 0 har du till:
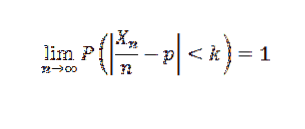
Provstorlek
När det gäller variansen tillåter Chebyshov-ojämlikheten oss att hitta ett provstorlek n som är tillräckligt för att garantera att sannolikheten att | Sn-μ |> = k uppträder är så liten som önskat, vilket gör att vi kan ha en approximation genomsnitt.
Låt X1, X2, ... Xn vara ett urval av oberoende slumpmässiga variabler av storlek n och antag att E (Xi) = μ och dess varians σtvå. Så, genom Chebyshovs ojämlikhet har vi:
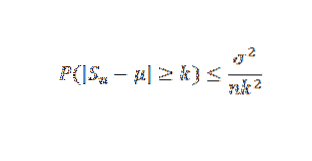
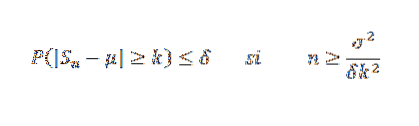
Exempel
Antag att X1, X2, ... Xn är ett urval av oberoende slumpmässiga variabler med Bernoulli-fördelning, så att de tar värdet 1 med sannolikhet p = 0,5.
Vad bör vara storleken på provet för att kunna garantera att sannolikheten att skillnaden mellan det aritmetiska medelvärdet Sn och dess förväntade värde (överstiger mer än 0,1) är mindre än eller lika med 0., 01?
Lösning
Vi har det E (X) = μ = p = 0,5 och att Var (X) = σtvå= p (1-p) = 0,25. Av Chebyshovs ojämlikhet har vi för alla k> 0:
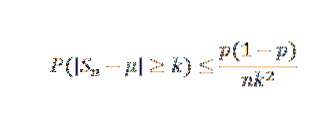
Nu med k = 0,1 och δ = 0,01 har vi:
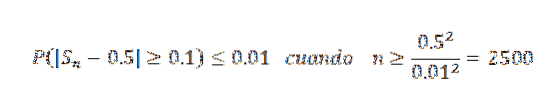
På detta sätt dras slutsatsen att en provstorlek på minst 2500 behövs för att garantera att sannolikheten för händelsen | Sn - 0,5 |> = 0,1 är mindre än 0,01.
Ojämlikheter av Chebyshov-typ
Det finns flera ojämlikheter relaterade till Chebyshovs ojämlikhet. En av de mest kända är Markovs ojämlikhet:
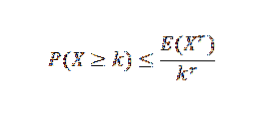
I detta uttryck är X en icke-negativ slumpmässig variabel med k, r> 0.
Markovs ojämlikhet kan ha olika former. Låt till exempel Y vara en icke-negativ slumpmässig variabel (så P (Y> = 0) = 1) och antag att E (Y) = μ existerar. Antag också att (E (Y))r= μr finns för vissa heltal r> 1. Sedan:
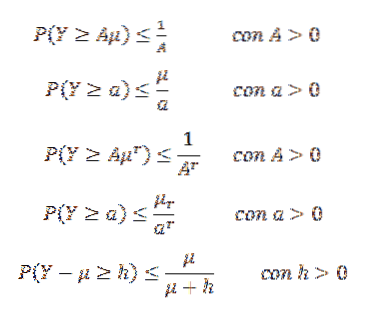
En annan ojämlikhet är Gaussian, som berättar att givet en unimodal slumpmässig variabel X med läge på noll, sedan för k> 0,
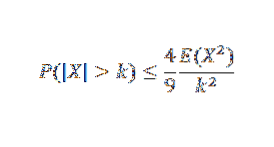
Referenser
- Kai Lai Chung. Elementär möjlighetsteori med stokastiska processer. Springer-Verlag New York Inc.
- Kenneth H. Rosen. Diskret matematik och dess tillämpningar. S.A. MCGRAW-HILL / INTERAMERICANA DE ESPAÑA.
- Paul L. Meyer. Sannolikhet och statistiska tillämpningar. S.A. MEXIKANSKA ALHAMBRA.
- Seymour Lipschutz Ph.D. 2000 Lösta problem med diskret matematik. McGRAW-HILL.
- Seymour Lipschutz Ph.D. Teori och sannolikhetsproblem. McGRAW-HILL.


Ingen har kommenterat den här artikeln än.