
Thévenins sats vad den består av, applikationer och exempel
De Thévenins sats anger att en krets med terminalerna A och B kan ersättas med en ekvivalent som består av en källa och ett seriemotstånd, vars värden ger samma potentialskillnad mellan A och B och samma impedans som den ursprungliga kretsen.
Denna teorem gjordes känd 1883 av den franska ingenjören Léon Charles Thévenin, men det hävdas att den förklarades trettio år tidigare av den tyska fysikern Hermann von Helmholtz.

Dess användbarhet ligger i det faktum att, även när den ursprungliga kretsen är komplex eller okänd, för en belastning eller impedans som placeras mellan terminalerna A och B, fungerar den enkla Thévenin-ekvivalenta kretsen på samma sätt som originalet.
Artikelindex
- 1 Hur beräknar du motsvarande spänning steg för steg?
- 1.1 - Experimentellt
- 1.2 - Lösa kretsen
- 2 Tillämpningar av Thévenins teorem (del I)
- 2.1 Exempel 1a (beräkning av motsvarande spänning steg för steg)
- 2.2 Exempel 1b (ström i lasten med Thévenin-ekvivalenten)
- 3 Bevis på Thévenins teorem
- 4 Tillämpning av Thévenins teorem (del II)
- 4.1 Exempel 2a (motsvarighet mot Thévenin-ekvivalent)
- 4.2 Exempel 2b
- 4.3 Exempel 2c
- 5 Tillämpning av Thévenins teorem (del III)
- 5.1 Exempel 3
- 6 Referenser
Hur beräknar du motsvarande spänning steg för steg?
Spänningen eller potentialskillnaden för motsvarande krets kan erhållas på följande sätt:
- Experimentellt
Skaffa motsvarande Théveninspänning
Om det är en enhet eller utrustning som är i en “svart låda” mäts potentialskillnaden mellan plintarna A och B med en voltmeter eller ett oscilloskop. Det är mycket viktigt att ingen belastning eller impedans placeras mellan plintarna A och B.
En voltmeter eller ett oscilloskop representerar ingen belastning på terminalerna, eftersom båda enheterna har en mycket stor impedans (helst oändlig) och det skulle vara som om terminalerna A och B var utan belastning. Spänningen eller spänningen som erhålls på detta sätt är motsvarande Thévenin-spänning.
Att erhålla Thévenins motsvarande impedans
För att erhålla motsvarande impedans från en experimentell mätning placeras ett känt motstånd mellan plintarna A och B och spänningsfallet eller spänningssignalen mäts med ett oscilloskop..
Från spänningsfallet i det kända motståndet mellan terminalerna kan strömmen som strömmar genom den erhållas.
Produkten av strömmen erhållen med ekvivalent motstånd plus spänningsfallet uppmätt i det kända motståndet är lika med motsvarande Théveninspänning som tidigare erhållits. Från denna jämställdhet rensas den motsvarande Thévenin-impedansen.
- Lösa kretsen
Beräkning av Thévenins ekvivalenta spänning
För det första kopplas all belastning eller impedans från plintarna A och B.
Som kretsen är känd tillämpas nätteori eller Kirchhoffs lagar för att hitta spänningen vid terminalerna. Denna spänning kommer att motsvara Thévenin.
Beräkning av Thévenins ekvivalenta impedans
För att få motsvarande impedans fortsätter vi till:
- Byt ut originalkretsens spänningskällor med kortslutningar "nollimpedans" och strömkällorna i originalkretsen med öppna "oändlig impedans".
- Därefter beräknas motsvarande impedans enligt reglerna för serieimpedanser och parallella impedanser.
Tillämpningar av Thévenins teorem (del I)
Vi kommer att tillämpa Thévenins sats för att lösa några kretsar. I denna första del betraktar vi en krets som endast har spänningskällor och motstånd.
Exempel 1a (beräkning av ekvivalent belastning steg för steg)
Figur 2 visar kretsen som finns i en himmelsk låda som har två elektromotoriska kraftbatterier V1 respektive V2 och motstånd R1 och R2, kretsen har anslutningarna A och B där en belastning kan anslutas.
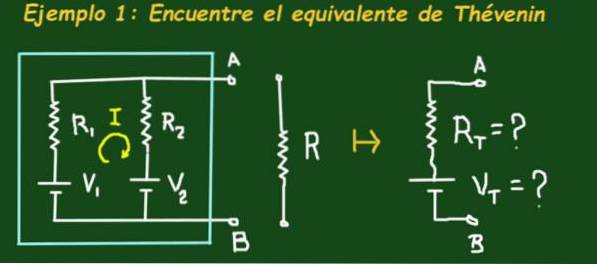
Målet är att hitta Thévenins ekvivalenta krets, det vill säga att bestämma Vt- och Rt-värdena för motsvarande krets. Använd följande värden: V1 = 4V, V2 = 1V, R1 = 3Ω, R2 = 6Ω och R = 1Ω.
Steg för steg-lösning
Steg 1
Vi bestämmer spänningen vid plintarna A och B när ingen belastning läggs på dem.
Steg 2
Kretsen som ska lösas består av ett enda nät genom vilket en ström I cirkulerar som vi har tagit positivt medurs.
Steg 3
Vi går igenom nätet och börjar med det nedre vänstra hörnet. Banan leder till följande ekvation:
V1 - I * R1 - I * R2 - V2 = 0
Steg 4
Vi löser nätströmmen I och får:
I = (V1-V2) / (R1 + R2) = (4V - 1V) / (3Ω + 6Ω) = ⅓ A
Steg 5
Med nätströmmen kan vi bestämma spänningsskillnaden mellan A och B, vilket är:
Vab = V1 - I * R1 = 4V - ⅓ A * 3Ω = 3V
Det vill säga, Thevenin-ekvivalentspänningen är: Vt = 3V.
Steg 6 (Thévenin ekvivalent motstånd)
Vi fortsätter nu med att beräkna Thévenins ekvivalenta motstånd, för vilket och som tidigare nämnts ersätts spänningskällorna med en kabel.
I så fall har vi bara två motstånd parallellt, så Thévenins ekvivalenta motstånd är:
Rt = (R1 * R2) / (R1 + R2) = (3Ω * 6Ω) / (3Ω + 6Ω) = 2Ω
Exempel 1b (ström i lasten med Thévenin-ekvivalenten)
Anslut som en belastning till plintarna A och B ett motstånd R = 1Ω till motsvarande krets och hitta strömmen som strömmar genom nämnda belastning.
Lösning
När motståndet R är anslutet till Thevenin-ekvivalenta kretsen har vi en enkel krets som består av en källa Vt ett motstånd Rt i serie med motståndet R.
Vi kommer att kalla Ic strömmen som flyter genom lasten R, så att nätekvationen ser ut så här:
Vt - Ic * Rt - Ic * R = 0
varifrån det följer att Ic ges av:
Ic = Vt / (Rt + R) = 3V / (2Ω + 1Ω) = 1 A
Bevis på Thévenins teorem
För att verifiera att Thévenins sats håller, anslut R till den ursprungliga kretsen och hitta strömmen som flyter genom R genom att tillämpa nätlagen på den resulterande kretsen.
Den resulterande kretsen förblir och dess nätekvationer förblir som visas i följande bild:
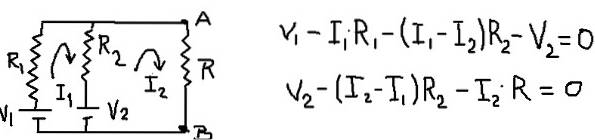
Genom att lägga till nätekvationerna är det möjligt att hitta nätströmmen I1 som en funktion av strömmen I2. Sedan ersätts den med den andra nätekvationen och en ekvation lämnas med I2 som den enda okända. Följande tabell visar operationerna.
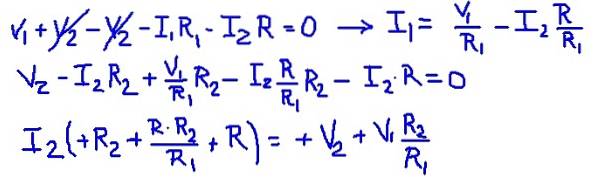
Därefter ersätts värdena för källans motstånd och spänningar, vilket ger det numeriska värdet för nätströmmen I2.

Nätströmmen I2 är strömmen som strömmar genom belastningsmotståndet R och värdet som hittas av 1 A sammanfaller helt med det som tidigare hittats med motsvarande Thévenin-krets..
Tillämpning av Thévenins sats (del II)
I denna andra del kommer Thévenin-satsen att tillämpas i en krets som har spänningskällor, strömkälla och motstånd.
Exempel 2a (Thévenin ekvivalent motstånd)
Målet är att bestämma Thévenin-ekvivalenta kretsen som motsvarar kretsen i följande figur, när terminalerna är utan motstånd på 1 ohm, placeras motståndet och strömmen som cirkulerar genom den bestäms.
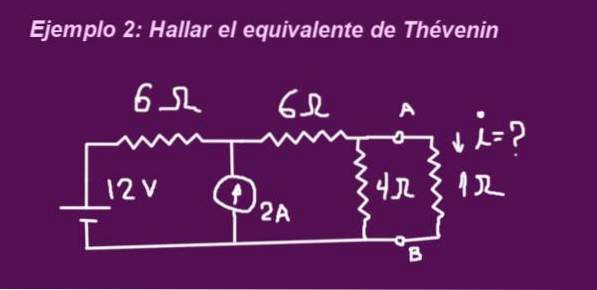
Lösning
För att hitta motsvarande motstånd, ta bort lastmotståndet (i detta fall 1 ohm). Dessutom ersätts spänningskällor med en kortslutning och strömkällor med en öppen krets..
På detta sätt är kretsen för vilken motsvarande motstånd kommer att beräknas den som visas nedan:
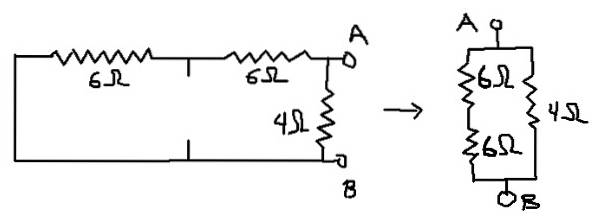
Rab = (12Ω * 4Ω) / (12Ω + 4Ω) = 3Ω vilket är Thevenin-ekvivalent motstånd (Rth).
Exempel 2b
Beräkna Thévenins ekvivalenta spänning.
Lösning
För att beräkna Thévenins ekvivalenta spänning överväger vi följande krets, där vi placerar strömmarna i I1 och I2 i grenarna som anges i följande bild:
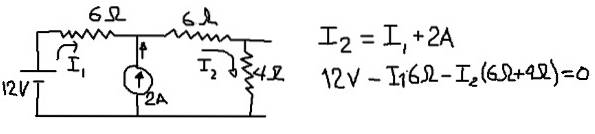
Den föregående figuren visar ekvationen för strömnoderna och ekvationen av spänningar när det yttre nätet passeras. Från den andra ekvationen rensas nuvarande I1:
I1 = 2 - I2 * (5/3)
Denna ekvation är ersatt med ekvationen av noderna:
I2 = 2 - (5/3) I2 + 2 ===> I2 (8/3) = 4 ===> I2 = 12/8 = 1,5 A
Detta innebär att spänningsfallet över 4 ohm-motståndet är 6 volt..
Kort sagt är Thévenins spänning Vth = 6 V..
Exempel 2c
Hitta Thevenin-ekvivalent krets och ström i lastmotståndet.
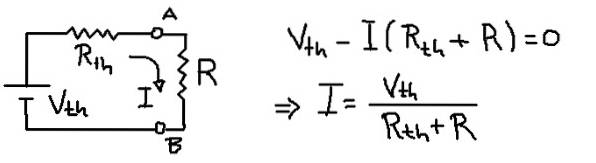
Lösning
Föregående figur visar Thévenins ekvivalenta krets med belastningsmotståndet R. Från spänningsekvationen i nätet dras strömmen I som strömmar genom belastningsmotståndet R.
I = Vth / (Rth + R) = 6V / (3Ω + 1Ω) = 1,5 A
Tillämpning av Thévenins teorem (del III)
I denna tredje del av tillämpningen av Thévenins sats betraktas en växelströmskrets som innehåller en växelspänningskälla, en kondensator, en induktans och ett motstånd..
Exempel 3
Målet är att hitta Thévenin Circuit motsvarande följande krets:
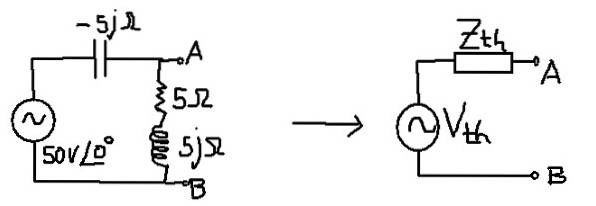
Lösning
Den ekvivalenta impedansen motsvarar kondensatorns parallell med seriekombinationen av motstånd och induktans.
Det motsatta av motsvarande impedans ges av:
Zeq ^ -1 = (-5j) ^ - 1 + (5 + 5j) ^ - 1 = (1/5) j + ((1/10 + (1/10) j) = (1/10 + 3 / 10 j) Mho
Och motsvarande impedans blir då:
Zeq = (1-3 j) Ohm
Den komplexa strömmen I kan härledas från nätekvationen:
50V∠0 - I (-5 j + 5 + 5j) = 50V∠0 - I * 5 = 0 ===> I = 10A ∠0
Nu beräknas spänningsfallet i motståndet plus induktansen, det vill säga spänningen Vab som kommer att motsvara Thévenins spänning:
Vab = I * (5 + 5 j) Ω = 10A ∠0 * 5Ω∠45º = 50V∠45º
Med andra ord har motsvarande spänning samma toppvärde som den ursprungliga källan men är 45 grader ur fas: Vth = 50V∠45º
Referenser
- Elektronikhandledning, Thevenins teorem. Återställd från: electronics-tutorials.ws
- Frågor och svar om nätverksteori. Thevenins sats. Återställd från: sanfoundry.com
- Thevenins teorem. Steg för steg-procedur. Återställd från: electrictechnology.org
- Thevenins sats. Löst exempel steg för steg. Återställd från: electricsimple.blogspot.com
- Workshop om Thevenins och Nortons satser. Återställd från: web.iit.edu
- Wikipedia. Thévenins sats. Återställd från: wikipedia.com



Ingen har kommenterat den här artikeln än.