
Grundläggande sats för aritmetiska bevis, tillämpningar, övningar

De Den grundläggande satsen för aritmetik säger att alla naturliga tal större än 1 kan sönderdelas som en produkt av primtal - vissa kan upprepas - och denna form är unik för det numret, även om faktornas ordning kan vara annorlunda.
Kom ihåg att ett primtal sid Det är den som bara erkänner sig själv och 1 som positiva delare. Följande siffror är primära: 2, 3, 5, 7, 11, 13 och så vidare, eftersom det finns oändligheter. Siffran 1 anses inte vara en primär, eftersom den har en enda delare.

För deras del kallas numren som inte överensstämmer med ovanstående sammansatta nummer, som 4, 6, 8, 9, 10, 12, 14 ... Låt oss ta talet 10 till exempel och omedelbart ser vi att det kan sönderdelas som en produkt av 2 och 5:
10 = 2 × 5
Både 2 och 5 är faktiskt primtal. Satsen säger att detta är möjligt för valfritt nummer n:
Där s1, sidtvå, sid3... sr är primtal och k1, ktvå, k3,... kr de är naturliga tal. Så primtalen fungerar som tegelstenar från vilka de naturliga siffrorna byggs genom multiplikation.
Artikelindex
- 1 Bevis på aritmetikens grundläggande teorem
- 1.1 Unikhet med primfaktorisering
- 2 applikationer
- 2.1 Primtal i naturen
- 2.2 Primtal och online-shopping
- 3 Lösta övningar
- 3.1 - Övning 1
- 3.2 - Övning 2
- 4 Referenser
Bevis på den grundläggande satsen för aritmetik
Vi börjar med att visa att varje tal kan sönderdelas i huvudfaktorer. Låt vara ett naturligt tal n> 1, prime eller komposit.
Till exempel om n = 2 kan det uttryckas som: 2 = 1 × 2, vilket är primt. På samma sätt fortsätt med följande siffror:
3 = 1 × 3
4 = 2 × 2
5 = 1 × 5
6 = 2 × 3
7 = 1 × 7
8 = 2 × 2 × 2
Vi fortsätter så här och sönderdelar alla naturliga tal tills vi når siffran n -1. Låt oss se om vi kan göra det med följande nummer: n.
Om n är prim kan vi sönderdela det som n = 1 × n, men antag att n är sammansatt och har en delare d, logiskt sett mindre än n:
1< d < n.
Om n / d = p1, med P1 ett primtal, då skrivs n som:
n = p1.d
Om d är primärt finns inget mer att göra, men om det inte är så finns det ett nummer ntvå vilket är en delare av d och mindre än detta: ntvå < d, por lo que d podrá escribirse como el producto de ntvå med ett annat primtal stvå:
d = stvå ntvå
Att när man byter ut i det ursprungliga numret skulle n ge:
n = p1 .sidtvå .ntvå
Antag nu att ntvå antingen är ett primtal och vi skriver det som produkten av ett primtal p3, av en delare av dig n3, sådan att n3 < ntvå < n1 < n:
ntvå = s3.n3 → n = p1 sidtvå sid3.n3
Vi upprepar denna procedur ett begränsat antal gånger tills vi får:
n = p1.sidtvå.sid3 ... sr
Detta innebär att det är möjligt att sönderdelas alla heltal från 2 till n, som en produkt av primtal.
Unikhet med primär faktorisering
Låt oss nu verifiera att denna sönderdelning är unik med undantag för faktorernas ordning. Antag att n kan skrivas på två sätt:
n = p1.sidtvå.sid3 ... sr = q1.Vadtvå.Vad3... Vads (med r ≤ s)
Naturligtvis det1, Vadtvå, Vad3... är också primtal. Som sid1 dela a (q1.Vadtvå.Vad3... Vads) Sedan s1 är lika med något av "q", spelar det ingen roll till vilken, så vi kan säga att s1 = q1. Vi delar n med s1 och vi får:
sidtvå.sid3 ... sr =.Vadtvå.Vad3... Vads
Vi upprepar proceduren tills vi delar upp allt med sidr, då får vi:
1 = qr + 1... Vads
Men det går inte att komma till vadr + 1... Vads = 1 när r < s, solo si r = s. Aunque al admitir que r = s, también se admite que los “p” y los “q” son los mismos. Por lo tanto la descomposición es única.
Applikationer
Som vi har sagt tidigare representerar primtalen, om du vill, talens atomer, deras baskomponenter. Så den grundläggande satsen för aritmetik har många tillämpningar, den mest uppenbara: vi kan arbeta lättare med stora siffror om vi uttrycker dem som en produkt av mindre antal..
På samma sätt kan vi hitta den största gemensamma multipeln (LCM) och den största gemensamma delaren (GCF), ett förfarande som hjälper oss att göra summor av fraktioner lättare, hitta rötter av stora tal eller arbeta med radikaler, rationalisera och lösa applikationsproblem av mycket varierande karaktär.
Dessutom är primtal extremt gåtfulla. Ett mönster känns ännu inte igen i dem och det är inte möjligt att veta vilken som kommer nästa. Den största hittills hittades av datorer och har 24,862,048 siffror, även om de nya primtalen visas mindre ofta varje gång.
Primtal i naturen
Cikaderna, cikaderna eller cikaderna som bor i nordöstra USA kommer fram i cykler på 13 eller 17 år. De är båda primtal.
På detta sätt undviker cikaderna att sammanfalla med rovdjur eller konkurrenter som har andra födelseperioder, inte heller konkurrerar de olika sorterna av cikader med varandra, eftersom de inte sammanfaller under samma år..

Primtal och online shopping
Primtal används i kryptografi för att hålla kreditkortsinformation hemlig när du gör inköp via Internet. På detta sätt kommer informationen att köparen anländer exakt till butiken utan att gå vilse eller falla i händerna på skrupelfria människor..
Hur? Data på korten är kodade i ett tal N som kan uttryckas som produkten av primtal. Dessa primtal är nyckeln som uppgifterna avslöjar, men de är okända för allmänheten, de kan bara avkodas på webben som de riktas till.
Att sönderdela ett tal i faktorer är en lätt uppgift om siffrorna är små (se de lösta övningarna), men i detta fall används primtal på 100 siffror som en nyckel, som när man multiplicerar dem ger mycket större siffror, vars detaljerade sönderdelning innebär en stor uppgift.
Lösta övningar
- Övning 1
Sönderdela 1029 till huvudfaktorer.
Lösning
1029 är delbart med 3. Det är känt för att summan är en multipel av 3: 1 + 0 + 2 + 9 = 12 när man lägger till siffrorna. Eftersom faktornas ordning inte förändrar produkten kan vi börja där:
1029 3
343
1029 = 3 × 343
Å andra sidan 343 = 73, sedan:
1029 = 3 × 73 = 3 × 7 × 7 × 7
Och eftersom både 3 och 7 är primtal är detta sönderdelningen av 1029.
- Övning 2
Faktor för trinomial xtvå + 42x + 432.
Lösning
Trinomialen skrivs om i formen (x + a). (x + b) och vi måste hitta värdena för a och b, så att:
a + b = 42; a.b = 432
Siffran 432 sönderdelas i primfaktorer och därifrån väljs lämplig kombination genom försök och fel så att de tillagda faktorerna ger 42.
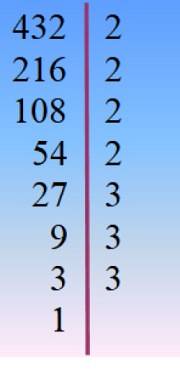
432 = 24 × 33 = 2 × 33× 23 = 24× 3två × 3 =…
Härifrån finns det flera möjligheter att skriva 432:
432 = 16 × 27 = 24 × 18 = 54 × 8 = 6 × 72 ... .
Och alla kan hittas genom att kombinera produkter mellan huvudfaktorerna, men för att lösa den föreslagna övningen är den enda lämpliga kombinationen: 432 = 24 × 18 sedan 24 + 18 = 42, då:
xtvå + 42x + 432 = (x + 24). (x +18)
Referenser
- Baldor, A. 1986. Teoretisk praktisk aritmetik. Compañía Cultural Editora de Textos Americanos S.A.
- BBC World. Den dolda naturkoden. Återställd från: bbc.com.
- De Leon, Manuel Prime-siffror: Internetets väktare. Återställd från: blogs.20minutos.es.
- UNAM. Number Theory I: Fundamental Theorem of Arithmetic. Återställd från: teoriadenumeros.wikidot.com.
- Wikipedia. Den grundläggande satsen för aritmetik. Återställd från: es.wikipedia.org.



Ingen har kommenterat den här artikeln än.