
Fourier-transformegenskaper, applikationer, exempel
De Fouriertransform är en metod för analytisk adekvat orienterad mot integrerbara funktioner som tillhör familjen tintegrerad omvandlad. Den består av en omdefiniering av funktioner F (t) i termer av Cos (t) och Sen (t).
De trigonometriska identiteterna för dessa funktioner, tillsammans med deras härlednings- och antideriveringsegenskaper, tjänar till att definiera Fourier-transformen genom följande komplexa funktion:
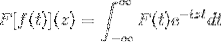
Vilket är sant så länge uttrycket är vettigt, det vill säga när den felaktiga integralen är konvergent. Algebraiskt sägs Fouriertransformen vara en linjär homeomorfism.
Varje funktion som kan arbetas med en Fourier-transform måste presentera null utanför en definierad parameter.
Artikelindex
- 1 Fastigheter
- 1.1 Existens
- 1.2 Fourier-transformationens linjäritet
- 1.3 Fouriertransform av ett derivat
- 1.4 Differentiering av Fourier-transformen
- 1.5 Fouriertransformation av en översättning
- 1.6 Översättning av Fouriertransformen
- 1.7 Fouriertransform av en skalagrupp
- 1.8 Symmetri
- 1.9 Fouriertransform av en faltningsprodukt
- 1.10 Kontinuitet och förfall till oändlighet
- 2 Historia
- 3 Vad är Fourier-transformationen för?
- 3.1 Fourier-serien
- 3.2 Andra former av Fourier-serien
- 4 applikationer
- 4.1 Beräkning av den grundläggande lösningen
- 4.2 Signalteori
- 5 Exempel
- 5.1 Exempel 1
- 5.2 Exempel 2
- 6 Föreslagna övningar
- 7 Referenser
Egenskaper

Fourier-transformen uppfyller följande egenskaper:
Existens
För att verifiera existensen av Fouriertransformationen i en funktion f (t) definierad i realerna R, följande två axiomer måste vara uppfyllda:
- f (t) är styckvis kontinuerligt för allt R
- f (t) är integrerbar i R
Fourier transformationslinjäritet
Låt M (t) och N (t) vara två funktioner med bestämda Fourier-transformationer, med alla konstanter a och b.
F [a M (t) + b N (t)] (z) = a F [M (t)] (z) + b F [NT Z)
Vilket stöds också av linjären hos integralen med samma namn.
Fouriertransform av ett derivat
Den har en funktion F som är kontinuerlig och integrerbar i alla realer, där:
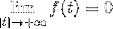
Och derivatet av f (f ') är kontinuerlig och definieras bitvis R
Fouriertransformationen av ett derivat definieras av integrering av delar, genom följande uttryck:
F [f '(t)] (z) = izF [f (t)] (z)
I högre ordensledningar kommer den att tillämpas på ett homologt sätt, där för alla n 1 har vi:
F [f n'(t)] (z) = (iz)nF [f (t)] (z)
Fourier transformdifferentiering
Den har en funktion F som är kontinuerlig och integrerbar i alla realer, där:
i (d / dz)F [f (t)] (z) = F [t. f (t)] (z)
Fouriertransform av en översättning
För alla θ som tillhör en uppsättning S och T som tillhör uppsättningen S ', har vi:
F [ τtill θ] = och-iay F [ θ] F [ τtillT ] = och-iax F [ T]
Med τtill arbetar som översättningsoperatör på vektorn a.
Översättning av Fouriertransformen
För alla θ som tillhör en uppsättning S och T som tillhör uppsättningen S ', har vi:
τtill F [θ] = F [och-iax.θ] τtill MED ] = F [och-iay . T]
För alla till som tillhör R
Fouriertransform av en skalagrupp
För alla θ som tillhör en uppsättning S. T som tillhör uppsättningen S '
λ tillhör R - 0 du måste:
F [θ (λx)] = (1 / | λ |) F [θ] (Y /λ)
F [T (λx)] = (1 / | λ |) F [T] (y / A)
Ja F är en kontinuerlig och tydligt integrerbar funktion, där a> 0. Sedan:
F [f (at)] (z) = (1 / a) F [f (t)] (z / a)
För att visa detta resultat kan vi fortsätta med ändringen av variabeln.
När T → + sedan s = vid → + ∞
När T → - då s = vid → - ∞
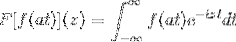
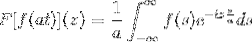
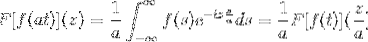
Symmetri
För att studera symmetrin för Fourier-transformen måste Parsevals identitet och Plancherel-formeln verifieras.
Vi har θ och δ som tillhör S. Därifrån kan man dra slutsatsen att:
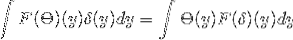
Kommer
1 / (2π)d F [θ ], F [5] Parsevals identitet
1 / (2π)d / 2 || F [θ ] ||LtvåRd Plancherel formel
Fouriertransform av en faltningsprodukt
För att uppnå liknande mål som i Laplace-transformen hänför sig funktionsklyvning till produkten mellan deras Fourier-transformer.
Vi har f och g som 2 begränsade, bestämda och helt integrerbara funktioner:
F (f * g) = F (f). F (g)
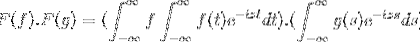
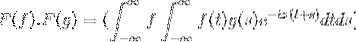
Sedan när du ändrar variabeln
t + s = x; det fortsätter med den felaktiga dubbla integralen
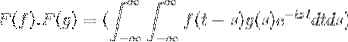
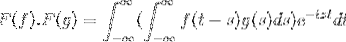
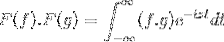
F (f). F (g) = F (f. G)
Kontinuitet och falla i oändligheten
För alla θ som tillhör R, F [ θ] följer kriterierna för en kontinuerlig funktion avgränsad i Rd.
Också F [ θ] (y) → 0 i C om | y | → ∞
Berättelse
Detta matematiska koncept presenterades av Joseph B. Fourier 1811 medan han utvecklade en avhandling om värmespridning. Det antogs snabbt av olika grenar av vetenskap och teknik.
Det etablerades som det huvudsakliga arbetsverktyget i studien av ekvationer med partiella derivat, även jämföra det med det befintliga arbetsförhållandet mellan Laplace-transformation och vanliga differentialekvationer.
Vad är Fourier-transformationen för?
Den tjänar främst till att väsentligt förenkla ekvationer, samtidigt som härledda uttryck omvandlas till kraftelement, vilket betecknar differentiella uttryck i form av integrerbara polynom..
Vid optimering, modulering och modellering av resultat fungerar det som ett standardiserat uttryck och är en frekvent resurs för teknik efter flera generationer.
Fourier-serien
De är serier definierade i termer av Cosines och Sines; De tjänar till att underlätta arbete med allmänna periodiska funktioner. När de används är de en del av teknikerna för att lösa vanliga och partiella differentialekvationer..
Fourier-serien är ännu mer generella än Taylor-serien, eftersom de utvecklar periodiska diskontinuerliga funktioner som inte har en Taylor-serierepresentation..
Andra former av Fourier-serien
För att förstå Fourier-transformationen analytiskt är det viktigt att granska de andra sätten på vilka Fourier-serien kan hittas tills vi kan definiera Fourier-serien i dess komplexa notation.
-Fourier-serier på en 2L-periodfunktion
Många gånger är det nödvändigt att anpassa strukturen för en Fourier-serie till periodiska funktioner vars period är p = 2L> 0 i intervallet [-L, L].
-Fourier-serier i udda och jämna funktioner
Intervallet [-π, π] beaktas, vilket ger fördelar när man utnyttjar funktionernas symmetriska egenskaper.
Om f är jämnt etableras Fourier-serien som en serie Cosines.
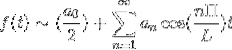
Om f är udda etableras Fourier-serien som en serie Sines.
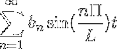
-Komplex notering av Fourier-serien
Om vi har en funktion f (t), som uppfyller alla utvecklingsbarhetskrav i Fourier-serien, är det möjligt att beteckna den i intervallet [-t, t] med dess komplexa notation:
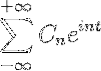
Applikationer

Beräkning av den grundläggande lösningen
Fouriertransformationen är ett kraftfullt verktyg i studien av partiella differentialekvationer av linjär typ med konstanta koefficienter. De gäller för funktioner med obegränsade domäner lika.
Liksom Laplace-transformen förvandlar Fourier-transformen en partiell derivatfunktion till en vanlig differentialekvation som är mycket enklare att använda..
Cauchy-problemet för värmeekvationen presenterar ett fält med frekvent tillämpning av Fourier-transform där funktionen genereras värmekärna eller Dirichlet-kärna.
När det gäller beräkningen av den grundläggande lösningen presenteras följande fall där det är vanligt att hitta Fourier-transformationen:
-Laplace-ekvation
-Värmeekvation
-Schrödinger ekvation
-Vågekvation
Signalteori
Den allmänna orsaken till tillämpningen av Fourier-transformen i denna gren beror främst på den karakteristiska nedbrytningen av en signal som en oändlig överlagring av lättare behandlingsbara signaler.
Det kan vara en ljudvåg eller en elektromagnetisk våg, Fourier-transformen uttrycker den i en superposition av enkla vågor. Denna framställning är ganska frekvent inom elektroteknik.
Å andra sidan finns det exempel på tillämpningen av Fourier-transformen inom signalteori:
-Systemidentifieringsproblem. Etablerat f och g
-Utgångssignalens konsistensproblem
-Problem med signalfiltrering
Exempel
Exempel 1
Definiera Fourier-transformationen för följande uttryck:
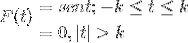
Vi kan också representera det på följande sätt:
F (t) = Sen (t) [H(t + k) - H(t - k) ]
Den rektangulära pulsen definieras:
p (t) = H(t + k) - H(t - k)
Fourier-transformen tillämpas på följande uttryck som liknar moduleringssatsen.
f (t) = p (t) Sen (t)
Var: F [w] = (1/2) i [p (w + 1) - p (w - 1)]
Och Fourier-transformen definieras av:
F [w] = (1/2) i [(2 / 2w + 1) Sen (k (w + 1)) - (2 / 2w + 1) Sen (k (w-1))]
Exempel 2
Definiera Fourier-transformen för uttrycket:
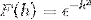
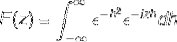
Eftersom f (h) är en jämn funktion kan det konstateras att
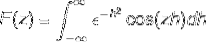
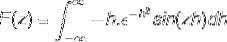
Integrering av delar tillämpas genom att välja variablerna och deras skillnader enligt följande
u = sin (zh) du = z cos (zh) dh
dv = h (e-h)två v = (e-h)två / två
Att ersätta du har
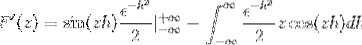
Efter utvärdering enligt den grundläggande satsen för kalkyl
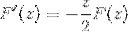
Genom att använda förkunskaper om första ordningens differenti ekvationer betecknas uttrycket som
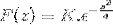
För att få K utvärderar vi
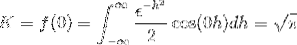
Slutligen definieras Fourier-transformen av uttrycket som
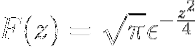
Föreslagna övningar
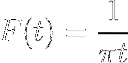
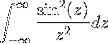
- Få transformationen av uttrycket W / (1 + wtvå)
Referenser
- Duoandikoetxea Zuazo, J., Fourier-analys. Addison- Wesley Iberoamericana, Autonomous University of Madrid, 1995.
- Lions, J. L., matematisk analys och numeriska metoder för vetenskap och teknik. Springer-Verlag, 1990.
- Lieb, E. H., Gaussiska kärnor har bara gaussiska maximerare. Uppfinna. Matematik. 102, 179-208, 1990.
- Dym, H., McKean, H. P., Fourier-serien och integraler. Academic Press, New York, 1972.
- Schwartz, L., Théorie des Distributions. Ed Hermann, Paris, 1966.


Ingen har kommenterat den här artikeln än.