
Laplace förvandla definition, historia och vad den är till för
De Laplace-omvandling Under de senaste åren har det varit av stor betydelse inom teknik-, matematik- och fysikstudier, bland andra vetenskapliga områden, eftersom det förutom att vara av stort teoretiskt intresse också ger ett enkelt sätt att lösa problem som kommer från vetenskap och teknik..
Ursprungligen presenterades Laplace-transformationen av Pierre-Simón Laplace i sin studie om sannolikhetsteori och behandlades ursprungligen som ett matematiskt objekt av rent teoretiskt intresse..

Nuvarande applikationer uppstår när olika matematiker försökte ge en formell motivering till de "operativa regler" som används av Heaviside i studien av ekvationer av elektromagnetisk teori..
Artikelindex
- 1 Definition
- 1.1 Exempel
- 1.2 Sats (tillräckliga förutsättningar för existens)
- 1.3 Laplace-transformation av några grundläggande funktioner
- 2 Historia
- 2.1 1782, Laplace
- 2.2 Oliver Heaviside
- 3 fastigheter
- 3.1 Linjäritet
- 3.2 Första översättningsteorem
- 3.3 Andra översättningsteorem
- 3.4 Skalförändring
- 3.5 Laplaces omvandling av derivat
- 3.6 Laplace-transformation av integraler
- 3.7 Multiplikation med tn
- 3.8 Uppdelning efter t
- 3.9 Periodiska funktioner
- 3.10 F (s) beteenden som s tenderar att vara oändliga
- 4 Omvända transformationer
- 4.1 Träning
- 5 Tillämpningar av Laplace-transform
- 5.1 Differentialekvationer
- 5.2 System med differentiella ekvationer
- 5.3 Mekanik och elektriska kretsar
- 6 Referenser
Definition
Låt f vara en funktion definierad för t ≥ 0. Laplace-transformen definieras enligt följande:
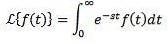
Laplace-transformation sägs existera om den tidigare integralen konvergerar, annars sägs det att Laplace-transform inte inte finns.
I allmänhet används små bokstäver för att beteckna funktionen som ska transformeras, och den stora bokstaven motsvarar dess transformation. På detta sätt kommer vi att ha:
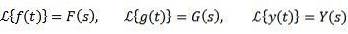
Exempel
Betrakta den konstanta funktionen f (t) = 1. Vi har att dess transform är:
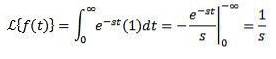
När integralen konvergerar, det vill säga när s> 0. Annars s < 0, la integral diverge.
Låt g (t) = t. Dess Laplace-transformation ges av
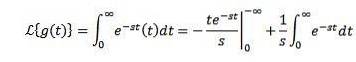
Genom att integrera med delar och veta att du-st tenderar till 0 när tenderar till oändlighet och s> 0, tillsammans med föregående exempel har vi:
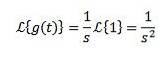
Transformationen kan existera eller inte, till exempel för funktionen f (t) = 1 / t konvergerar inte integralen som definierar dess Laplace-transformation och därför finns inte dess transformation.
De tillräckliga förutsättningarna för att garantera att Laplace-transformationen av en funktion f existerar är att f är kontinuerlig i delar för t ≥ 0 och är av exponentiell ordning.
En funktion sägs vara styckvis kontinuerlig för t ≥ 0, när det för ett intervall [a, b] med a> 0 finns ett ändligt antal punkter tk, där f har diskontinuiteter och är kontinuerligt i varje delintervall [tk-1,tk].
Å andra sidan sägs det att en funktion är av exponentiell ordning c om det finns verkliga konstanter M> 0, c och T> 0 så att:
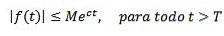
Som exempel har vi att f (t) = ttvå är av exponentiell ordning, eftersom | ttvå| < e3t för alla t> 0.
På ett formellt sätt har vi följande sats
Sats (tillräckliga förutsättningar för existens)
Om f är en delkontinuerlig funktion för t> 0 och av exponentiell ordning c, finns Laplace-transform för s> c.
Det är viktigt att notera att detta är ett villkor för tillräcklighet, det vill säga det kan vara så att det finns en funktion som inte uppfyller dessa villkor och ändå existerar dess Laplace-transformation.
Ett exempel på detta är funktionen f (t) = t-1/2 som inte är styckvis kontinuerlig för t ≥ 0 men dess Laplace-transform finns.
Laplace-transformation av några grundläggande funktioner
Följande tabell visar Laplace-transformationer av de vanligaste funktionerna.

Berättelse
Laplace-transformationen är skyldig Pierre-Simon Laplace, en fransk matematiker och teoretisk astronom som föddes 1749 och dog 1827. Hans berömmelse var sådan att han var känd som Newton i Frankrike.
År 1744 ägnade Leonard Euler sina studier till integraler med formuläret
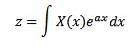
som lösningar på vanliga differentialekvationer, men han övergav snabbt denna undersökning. Senare undersökte Joseph Louis Lagrange, som mycket beundrade Euler, också denna typ av integraler och relaterade dem till sannolikhetsteorin.
1782, Laplace
År 1782 började Laplace studera dessa integraler som lösningar på differentialekvationer och enligt historiker bestämde han sig 1785 för att omformulera problemet, vilket senare gav upphov till Laplace-transformationerna som de förstås idag..
Efter att ha introducerats inom området sannolikhetsteori var det av lite intresse för tidens forskare och sågs bara som ett matematiskt objekt med endast teoretiskt intresse..
Oliver Heaviside
Det var i mitten av 1800-talet när den engelska ingenjören Oliver Heaviside upptäckte att differentiella operatörer kan behandlas som algebraiska variabler, vilket ger Laplace förvandlar deras moderna applikation..
Oliver Heaviside var en engelsk fysiker, elektrotekniker och matematiker som föddes i London 1850 och dog 1925. Medan han försökte lösa differentialekvationsproblem som tillämpades på vibrationsteorin och med hjälp av Laplaces studier började han forma de moderna tillämpningarna av Laplace-transformer..
De resultat som presenterades av Heaviside spred sig snabbt i hela vetenskapssamhället, men eftersom hans arbete inte var rigoröst kritiserades han snabbt av de mer traditionella matematikerna..
Men användbarheten av Heavisides arbete för att lösa fysiska ekvationer gjorde hans metoder populära bland fysiker och ingenjörer..
Trots dessa motgångar och efter några decennier av misslyckade försök, i början av 1900-talet kunde en rigorös motivering ges till de operativa regler som Heaviside gav..
Dessa försök bar frukt tack vare ansträngningarna från olika matematiker som Bromwich, Carson, van der Pol, bland andra..
Egenskaper
Bland egenskaperna hos Laplace-transformen sticker följande ut:
Linjäritet
Låt c1 och c2 vara konstanta och f (t) och g (t) -funktioner vars Laplace-transform är F (s) respektive G (s), då har vi:
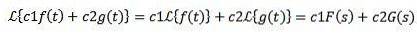
På grund av denna egenskap sägs Laplace-transformen vara en linjär operatör.
Exempel
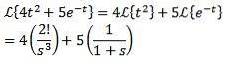
Första översättningssatsen
Om det händer att:
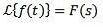
Och 'a' är vilket som helst verkligt tal, så:
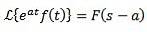
Exempel
Eftersom Laplace-transformationen av cos (2t) = s / (s ^ 2 + 4) då:
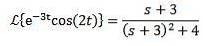
Andra översättningssatsen
Ja
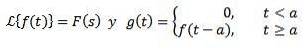
Sedan
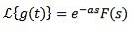
Exempel
Om f (t) = t ^ 3 är F (s) = 6 / s ^ 4. Och därför omvandlingen av
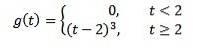
är G (s) = 6e-2s/ s ^ 4
Skalförändring
Ja
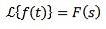
Och 'a' är en icke-nollverklig, det måste vi
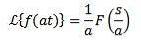
Exempel
Eftersom transformationen av f (t) = sin (t) är F (s) = 1 / (s ^ 2 + 1) har vi
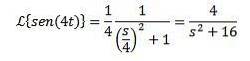
Laplace-transformation av derivat
Om f, f ', f ",…, f(n) är kontinuerliga för t ≥ 0 och är av exponentiell ordning och f(n)(t) är styckvis kontinuerligt för t ≥ 0, då
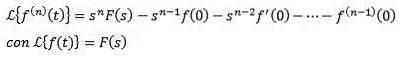
Laplace-transformation av integraler
Ja
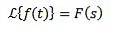
Sedan
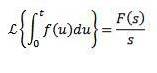
Multiplikation med tn
Om vi måste
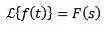
Sedan
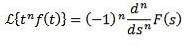
Uppdelning efter t
Om vi måste
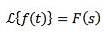
Sedan
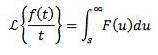
Periodiska funktioner
Låt f vara en periodisk funktion med period T> 0, det vill säga f (t + T) = f (t),
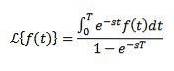
F (s) beteende som s tenderar till oändlighet
Om f är kontinuerligt i delar och i exponentiell ordning och
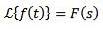
Sedan
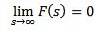
Inversa omvandlingar
När vi applicerar Laplace-transformen till en funktion f (t) får vi F (s), som representerar nämnda transform. På samma sätt kan vi säga att f (t) är den inversa Laplace-transformationen av F (s) och skrivs som
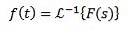
Vi vet att Laplace-transformationerna av f (t) = 1 och g (t) = t är F (s) = 1 / s och G (s) = 1 / stvå respektive, därför måste vi
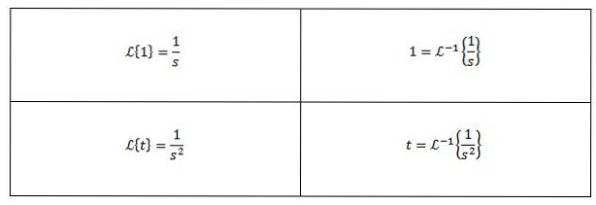
Några vanliga inversa Laplace-transformationer är som följer

Dessutom är den inversa Laplace-transformen linjär, det vill säga det är sant att
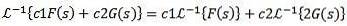
Övning
Hitta
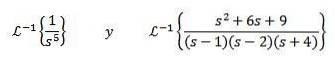
För att lösa denna övning måste vi matcha funktionen F (s) med en av föregående tabell. I det här fallet, om vi tar n + 1 = 5 och använder linjäritetsegenskapen för den inversa transformen, multiplicerar vi och delar med 4! Kommer
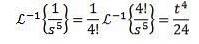
För den andra inversa transformen tillämpar vi partiella fraktioner för att skriva om funktionen F (s) och sedan linjäritetsegenskapen för att erhålla
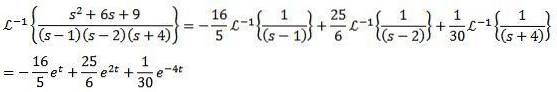
Som vi kan se från dessa exempel är det vanligt att funktionen F (s) som utvärderas inte exakt matchar någon av funktionerna i tabellen. För dessa fall räcker det, som framgår, att skriva om funktionen tills den når rätt form.
Tillämpningar av Laplace-transform
Differentiella ekvationer
Den huvudsakliga tillämpningen av Laplace-transformationer är att lösa differentialekvationer.
Med hjälp av transformegenskapen för ett derivat är det tydligt att
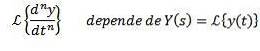
Och av n-1-derivaten utvärderade vid t = 0.
Denna egenskap gör transformationen mycket användbar för att lösa initialvärdesproblem där differentialekvationer med konstanta koefficienter är inblandade..
Följande exempel visar hur man använder Laplace-transformen för att lösa differentialekvationer.
Exempel 1
Med tanke på följande initialvärde problem
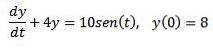
Använd Laplace-transformen för att hitta lösningen.
Vi tillämpar Laplace-transformen på varje del av differentialekvationen
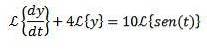
Genom egenskapen till transformationen av ett derivat har vi
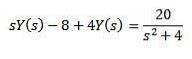
Genom att utveckla allt uttryck och rensa Y (ar) är vi kvar
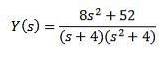
Använda partiella bråk för att skriva om den högra sidan av ekvationen vi får
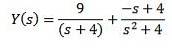
Slutligen är vårt mål att hitta en funktion y (t) som uppfyller differentialekvationen. Genom att använda den omvända Laplace-transformationen får vi resultatet
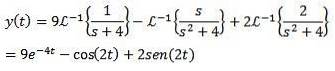
Exempel 2
Lösa
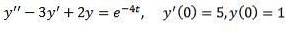
Som i föregående fall tillämpar vi transformationen på båda sidor av ekvationen och separerar term för term.
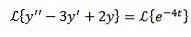
På detta sätt har vi som ett resultat
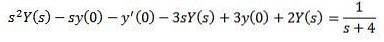
Ersätta med givna initialvärden och lösa för Y (s)
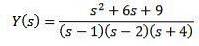
Med hjälp av enkla fraktioner kan vi skriva om ekvationen enligt följande
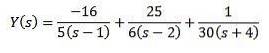
Och att applicera den omvända Laplace-transformationen ger oss resultatet
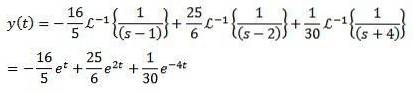
I dessa exempel kan du komma till fel slutsats att denna metod inte är mycket bättre än traditionella metoder för att lösa differentiella ekvationer..
Fördelarna med Laplace-transformationen är att du inte behöver använda parametervariation eller oroa dig för de olika fallen av den obestämda koefficientmetoden..
Dessutom, när vi löser inledande värdeproblem med den här metoden använder vi från början de ursprungliga villkoren, så det är inte nödvändigt att utföra andra beräkningar för att hitta den specifika lösningen.
System med differentiella ekvationer
Laplace-transformen kan också användas för att hitta lösningar på samtidiga vanliga differentialekvationer, som följande exempel visar.
Exempel
Sortera ut
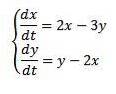
Med de initiala villkoren x (0) = 8 och y (0) = 3.
Om vi måste
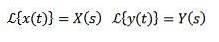
Sedan
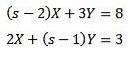
Lösning ger oss som ett resultat
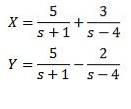
Och tillämpa den inversa Laplace-transform vi har
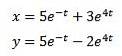
Mekanik och elektriska kretsar
Laplace-transformationen är av stor betydelse i fysik, den har huvudsakligen applikationer för mekanik och elektriska kretsar.
En enkel elektrisk krets består av följande element
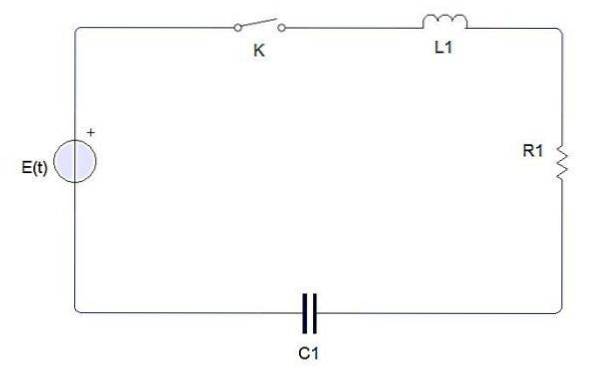
En omkopplare, ett batteri eller en källa, en induktor, ett motstånd och en kondensator. När omkopplaren är stängd alstras en elektrisk ström som betecknas med i (t). Kondensatorladdningen betecknas med q (t).
Enligt Kirchhoffs andra lag måste spänningen som produceras av källan E till den slutna kretsen vara lika med summan av var och en av spänningsfallet.
Den elektriska strömmen i (t) är relaterad till laddningen q (t) på kondensatorn med i = dq / dt. Å andra sidan definieras spänningsfallet i vart och ett av elementen enligt följande:
Spänningsfallet över ett motstånd är iR = R (dq / dt)
Spänningsfallet över en induktor är L (di / dt) = L (dtvåq / dttvå)
Spänningsfallet över en kondensator är q / C.
Med dessa data och tillämpning av Kirchhoffs andra lag på den enkla slutna kretsen erhålls en andra ordningens differentialekvation som beskriver systemet och låter oss bestämma värdet på q (t).
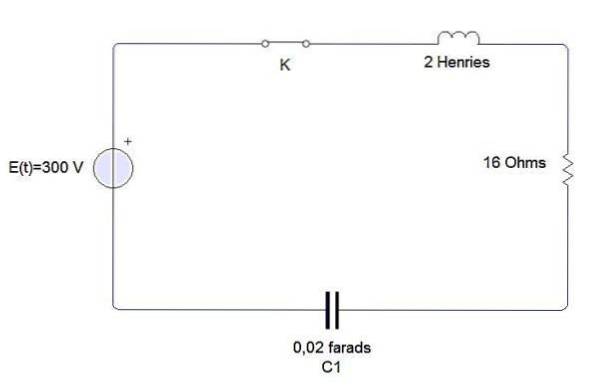
Exempel
En induktor, en kondensator och ett motstånd är anslutna till ett batteri E, som visas i figuren. Induktorn är 2 henries, kondensatorn är 0,02 farads och motståndet är 16 ohm. Vid tidpunkten t = 0 är kretsen stängd. Hitta laddningen och strömmen när som helst t> 0 om E = 300 volt.
Vi har att differentialekvationen som beskriver denna krets är följande
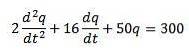
Där de initiala villkoren är q (0) = 0, i (0) = 0 = q '(0).
Genom att använda Laplace-transformen får vi det
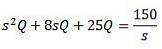
Och lösa för Q (t)
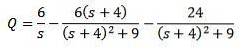
Sedan applicerar vi den omvända Laplace-transform som vi har
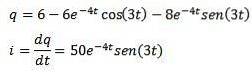
Referenser
- G. Holbrook, J. (1987). Laplace-transform för elektronikingenjörer. Limusa.
- Ruiz, L. M., & Hernandez, M. P. (2006). Differentialekvationer och Laplace-transform med applikationer. Ledare UPV.
- Simmons, G. F. (1993). Differentiella ekvationer med applikationer och historiska anteckningar. McGraw-Hill.
- Spiegel, M. R. (1991). Laplace förvandlas. McGraw-Hill.
- Zill, D. G. och Cullen, M. R. (2008). Differentiella ekvationer med gränsvärde problem. Cengage Learning Editores, S.A.



Ingen har kommenterat den här artikeln än.