
Trapezoid scaleneegenskaper, formler och ekvationer, exempel
A trapets scalene är en polygon med fyra sidor, varav två är parallella med varandra och med sina fyra inre vinklar av olika mått.
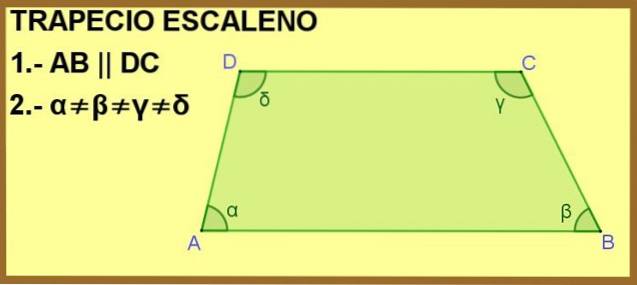
Fyrkanten ABCD visas nedan, där sidorna AB och DC är parallella med varandra. Detta räcker för att göra det till en trapes, men dessutom är de inre vinklarna α, β, γ och δ olika, varför trapezoid är skalen.
Artikelindex
- 1 Element av scalene trapezium
- 1.1 Andra trapezider
- 2 fastigheter
- 3 Formler och ekvationer
- 3.1 Höjd
- 3.2 Median
- 3.3 Diagonaler
- 3.4 Omkrets
- 3.5 Område
- 3.6 Andra förhållanden för scalene trapezium
- 4 Konstruktion av scalene trapez med linjal och kompass
- 5 Exempel
- 5.1 - Lösning a
- 5.2 - Lösning b
- 6 Övningen löst
- 6.1 Lösning
- 7 Referenser
Element av scalene trapezium
Här är de mest karakteristiska elementen:
-Basar och sidor: trapesens parallella sidor är dess baser och de två icke-parallella sidorna är sidorna.
I en scalene trapets är baserna av olika längd och de laterala också. En scalene trapezoid kan emellertid ha en lateral lika lång längd som en bas..
-Median: är det segment som förenar mittpunkterna för sidorna.
-Diagonaler: diagonalen för en trapes är det segment som förenar två motsatta hörn. En trapes har, liksom varje fyrkant, två diagonaler. I scalene trapezoid har de olika längd.
Andra trapezoider
Förutom scalene trapezoid finns det andra speciella trapezider: höger trapezoid och likbent trapezoid..
En trapets är en rektangel när en av dess vinklar är rätt, medan en likbent trapes har sina sidor av lika längd.
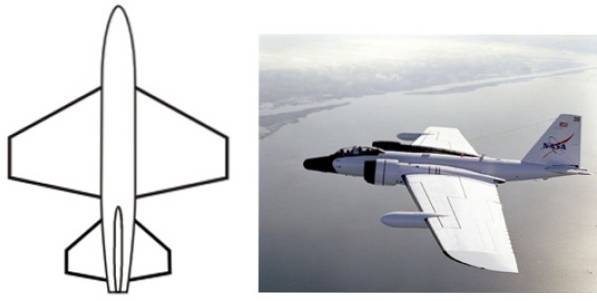
Den trapetsformade formen har många applikationer på design- och industrinivå, såsom i konfigurationen av flygplansvingar, formen på vardagliga föremål som bord, stolryggar, förpackningar, plånböcker, textiltryck och mer..
Egenskaper
Nedan listas egenskaperna för scalene trapezoid, varav många sträcker sig till andra typer av trapezoid. I det följande, när man talar om "trapezoid", kommer egenskapen att tillämpas på alla typer, inklusive scalene..
1. Trapezens median, det vill säga segmentet som förenar mittpunkterna på dess icke-parallella sidor, är parallellt med någon av baserna.
2. - Median för en trapez har en längd som är halvsumman av dess baser och skär dess diagonaler vid mittpunkten.
3.- Trapesformens diagonaler skär varandra vid en punkt som delar dem i två sektioner som är proportionella mot basernas kvoter.
4.- Summan av kvadraterna av diagonalerna för en trapets är lika med summan av kvadraten på dess sidor plus den dubbla produkten av dess baser..
5.- Segmentet som förenar mittpunkterna på diagonalerna har en längd som är lika med basens semidifferens.
6.- Vinklarna intill de laterala är kompletterande.
7.- I en scalene trapets är längden på dess diagonaler olika.
8. - En trapes har en inskriven omkrets endast om summan av dess baser är lika med summan av dess sidor.
9.- Om en trapets har en inskriven omkrets, är vinkeln med toppunkten i mitten av nämnda omkrets och sidor som passerar genom ändarna på sidan av trapesformen rak.
10.- En scalene trapez har inte en begränsad omkrets, den enda typen av trapez som har en är likbent.
Formler och ekvationer
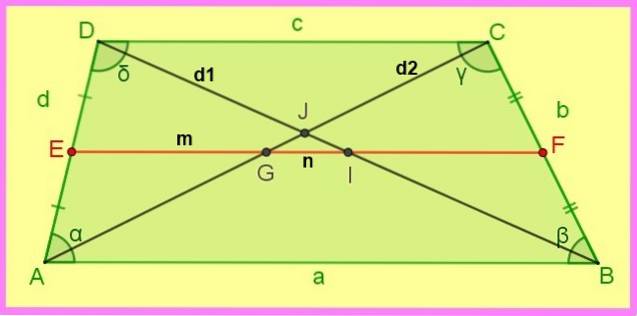
Följande förhållanden för den scalene trapezoid hänvisas till följande figur.
1.- Om AE = ED och BF = FC → EF || AB och EF || DC.
2.- EF = (AB + DC) / 2 det vill säga: m = (a + c) / 2.
3.- DI = IB = d1 / 2 och AG = GC = dtvå /två.
4.- DJ / JB = (c / a) på samma sätt CJ / JA = (c / a).
5.- DBtvå + ACtvå = ADtvå + före Kristustvå + 2 AB ∙ DC
Likvärdigt:
d1två + dtvåtvå = dtvå + btvå + 2 a ∙ c
6.- GI = (AB - DC) / 2
Nämligen:
n = (a - c) / 2
7.- a + δ = 180⁰ och β + y = 180⁰
8.- Om α ≠ β ≠ γ ≠ δ då d1 ≠ d2.
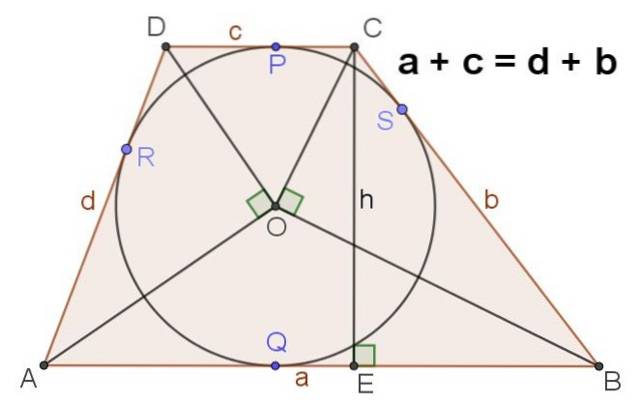
9.- Figur 4 visar en scalene trapezoid som har en inskriven omkrets, i detta fall är det sant att:
a + c = d + b
10. - I en scalene trapezoid ABCD med inskriven omkrets av centrum O gäller även följande:
∡AOD = ∡BOC = 90⁰
Höjd
Trapesens höjd definieras som det segment som går från en punkt av basen vinkelrätt mot motsatt bas (eller till dess förlängning).
Alla trapesens höjder har samma mätning h, så oftast avser ordets höjd mätningen. I syntesen är höjden avståndet eller separationen mellan baserna.
Höjden h kan bestämmas genom att känna till längden på en sida och en av vinklarna intill sidan:
h = d Sen (α) = d Sen (γ) = b Sen (β) = b Sen (δ)
Median
Måttet på trapezens median är halvsumman av baserna:
m = (a + b) / 2
Diagonaler
d1 = √ [atvå + dtvå - 2 ∙ a ∙ d ∙ Cos (α)]
dtvå= √ [atvå + btvå - 2 ∙ a ∙ b ∙ Cos (β)]
Det kan också beräknas om endast längden på trapetsformens sidor är känd:
d1 = √ [btvå + a ∙ c - a (btvå - dtvå) / (a - c)]
dtvå = √ [dtvå + a ∙ c - a (dtvå - btvå) / (a - c)]
Omkrets
Omkretsen är den totala längden på konturen, det vill säga summan av alla dess sidor:
P = a + b + c + d
Område
Området för en trapets är halvsumman av dess baser multiplicerat med dess höjd:
A = h ∙ (a + b) / 2
Det kan också beräknas om median m och höjd h är kända:
A = m ∙ h
Om endast längden på trapezoidens sidor är känd, kan området bestämmas med hjälp av Herons formel för trapezoid:
A = [(a + c) / | a-c |] ∙ √ [(s-a) (s-c) (s-a-d) (s-a-b)]
Där s är semiperimeter: s = (a + b + c + d) / 2.
Andra förhållanden för scalene trapezium
Korsningen av medianen med diagonalerna och parallellen som passerar genom skärningspunkten mellan diagonalerna ger upphov till andra relationer.
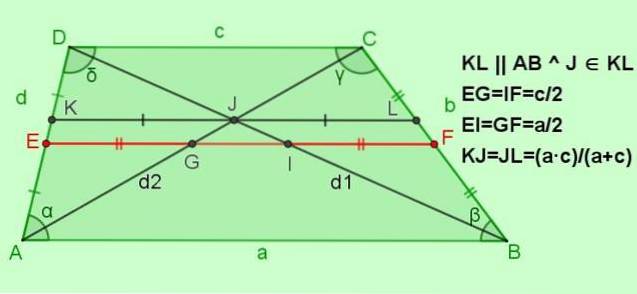
-Relationer för median EF
EF = (a + c) / 2; EG = IF = c / 2; EI = GF = a / 2
-Relationer för segmentet parallellt med baserna KL, och passerar genom punkten J skärningspunkten mellan diagonalerna
Om KL || AB || DC med J ∈ KL, sedan KJ = JL = (a ∙ c) / (a + c)
Konstruktion av den scalene trapez med linjal och kompass
Med tanke på längdbaserna till Y c, där a> c och med sidor av längderna b och d, varelse b> d, fortsätt med dessa steg (se figur 6):
1.- Med regeln ritas segmentet för större AB.
2. - Från A se och på AB markeras punkten P så att AP = c.
3.- Med kompassen med centrum vid P och radie d ritas en båge.
4.- Centrera vid B med radie b och dra en båge som fångar upp bågen som ritades i föregående steg. Vi kallar Q skärningspunkten.
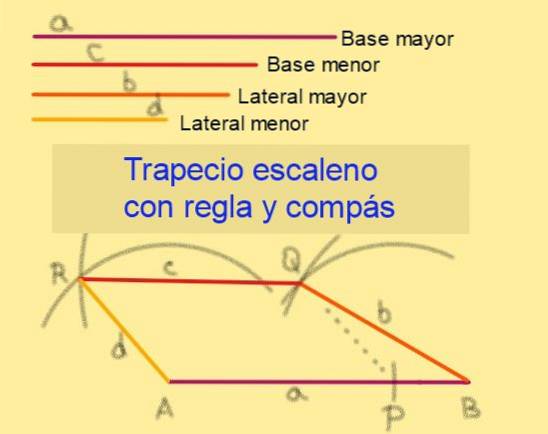
5.- Med mitten vid A, rita en båge med radien d.
6. - Med mitten vid Q, rita en båge med radie c som avlyssnar bågen som ritades i föregående steg. Skärpunkten kommer att kallas R.
7. - Segment BQ, QR och RA spåras med linjalen.
8.- Det fyrsidiga ABQR är en scalene trapezoid, eftersom APQR är ett parallellogram som garanterar att AB || Qr.
Exempel
Följande längder anges i cm: 7, 3, 4 och 6.
a) Bestäm om det med dem är möjligt att konstruera en scalene trapez som kan omge en cirkel.
b) Hitta omkretsen, arean, längden på diagonalerna och trapezoidens höjd samt radien på den inskrivna cirkeln.
- Lösning till
Genom att använda segmenten längd 7 och 3 som baser och de med längd 4 och 6 som laterala kan en skalen trapetsform konstrueras med användning av proceduren som beskrivs i föregående avsnitt.
Det återstår att kontrollera om den har en inskriven omkrets, men kom ihåg egenskapen (9):
En trapets har endast en inskriven omkrets om summan av dess baser är lika med summan av dess sidor.
Vi ser det effektivt:
7 + 3 = 4 + 6 = 10
Då uppfylls villkoret för existensen av inskriven omkrets.
- Lösning b
Omkrets
Omkretsen P erhålls genom att lägga till sidorna. Eftersom baserna lägger till upp till 10 och sidorna också är omkretsen:
P = 20 cm
Område
För att bestämma området, känt endast dess sidor, tillämpas förhållandet:
A = [(a + c) / | a-c |] ∙ √ [(s-a) (s-c) (s-a-d) (s-a-b)]
Var s är semiperimeter:
s = (a + b + c + d) / 2.
I vårt fall är semiperimeter värt s = 10 cm. Efter att ha ersatt respektive värden:
a = 7 cm; b = 6 cm; c = 3 cm; d = 4 cm
Resterna:
A = [10/4] √ [(3) (7) (- 1) (- 3)] = (5/2) √63 = 19,84 cm ^.
Höjd
Höjden h är relaterad till området A med följande uttryck:
A = (a + c) ∙ h / 2, från vilken höjden kan erhållas genom att rensa:
h = 2A / (a + c) = 2 * 19,84 / 10 = 3,988 cm.
Radien på den inskrivna cirkeln
Radien på den inskrivna cirkeln är lika med halva höjden:
r = h / 2 = 1 984 cm
Diagonaler
Slutligen hittas längden på diagonalerna:
d1 = √ [btvå + a ∙ c - a (btvå - dtvå) / (a - c)]
dtvå = √ [dtvå + a ∙ c - a (dtvå - btvå) / (a - c)]
Genom att ersätta värdena korrekt har vi:
d1 = √ [6två + 7 ∙ 3 - 7 (6två - 4två) / (7 - 3)] = √ (36 + 21-7 (20) / 4) = √ (22)
dtvå = √ [4två + 7 ∙ 3 - 7 (4två - 6två) / (7 - 3)] = √ (16 + 21-7 (-20) / 4) = √ (72)
Det vill säga: d1 = 4,69 cm och dtvå = 8,49 cm
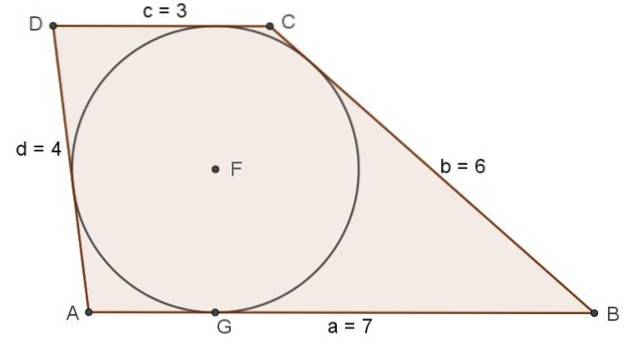
Övningen löst
Bestäm trapezoidens inre vinklar med baserna AB = a = 7, CD = c = 3 och sidovinklar BC = b = 6, DA = d = 4.
Lösning
Cosinosatsen kan tillämpas för att bestämma vinklarna. Till exempel bestäms vinkeln ∠A = α från triangeln ABD med AB = a = 7, BD = d2 = 8,49 och DA = d = 4.
Cosinussatsen som tillämpas på denna triangel ser ut så här:
dtvåtvå = atvå + dtvå - 2 ∙ a ∙ d ∙ Cos (α), det vill säga:
72 = 49 + 16-56 ∙ Cos (α).
Lösning för, erhålls cosinus för vinkel α:
Cos (a) = -1/8
Det vill säga α = ArcCos (-1/8) = 97,18⁰.
På samma sätt erhålls de andra vinklarna, deras värden är:
p = 41,41⁰; γ = 138,59⁰ och slutligen δ = 82,82⁰.
Referenser
- C. E. A. (2003). Element av geometri: med övningar och kompassens geometri. University of Medellin.
- Campos, F., Cerecedo, F. J. (2014). Matematik 2. Grupo Editorial Patria.
- Freed, K. (2007). Upptäck polygoner. Benchmark Education Company.
- Hendrik, V. (2013). Allmänna polygoner. Birkhäuser.
- IGER. (s.f.). Matematik första terminen Tacaná. IGER.
- Jr. geometri. (2014). Polygoner. Lulu Press, Inc..
- Miller, Heeren och Hornsby. (2006). Mathematics: Reasoning And Applications (tionde upplagan). Pearson Education.
- Patiño, M. (2006). Matematik 5. Redaktionellt program.
- Wikipedia. Trapets. Återställd från: es.wikipedia.com


Ingen har kommenterat den här artikeln än.