De akuta trianglar är de vars tre inre vinklar är spetsiga vinklar; dvs måttet på var och en av dessa vinklar är mindre än 90 ° grader. Genom att inte ha någon rätt vinkel har vi att den pythagoreiska satsen inte håller för denna geometriska figur.
Därför, om vi vill ha någon form av information om någon av dess sidor eller vinklar, är det nödvändigt att använda andra satser som tillåter oss att få tillgång till nämnda data. De vi kan använda är sinussatsen och cosinussatsen.
Artikelindex
Bland de egenskaper som denna geometriska figur har kan vi lyfta fram de som ges av det enkla faktum att vara en triangel. Bland dessa har vi:
- En triangel är en polygon som har tre sidor och tre vinklar.
- Summan av dess tre inre vinklar är lika med 180 °.
- Summan av två av dess sidor är alltid större än den tredje.
Som ett exempel, låt oss titta på följande triangel ABC. På ett allmänt sätt identifierar vi dess sidor med små bokstäver och dess vinklar med stora bokstäver, på ett sådant sätt att ena sidan och dess motsatta vinkel har samma bokstav.
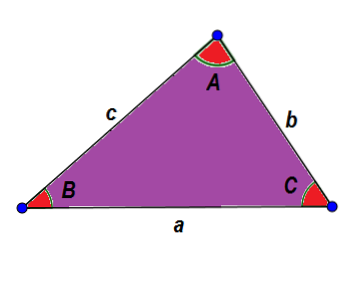
Från de redan angivna egenskaperna vet vi att:
A + B + C = 180 °
a + b> c, a + c> b och b + c> a
Huvudegenskapen som skiljer denna typ av triangel från resten är att, som vi redan nämnde, dess inre vinklar är spetsiga; dvs måttet på var och en av dess vinklar är mindre än 90 °.
Akuta trianglar, tillsammans med trubbiga trianglar (de där en av deras vinklar har ett mått större än 90 °), ingår i uppsättningen av sneda trianglar. Denna uppsättning består av trianglar som inte är raka vinklar.
Eftersom de sneda trianglarna är en del måste vi kunna lösa problem som involverar akuta trianglar, vi måste använda sinus-satsen och cosinus-satsen.
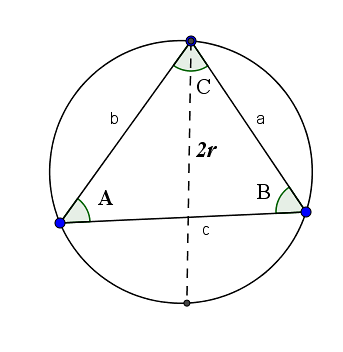
Sinussatsen berättar att förhållandet mellan en sida och sinus för dess motsatta vinkel är lika med två gånger radien för cirkeln som bildas av de tre hörnpunkterna i nämnda triangel. Nämligen:
2r = a / sin (A) = b / sin (B) = c / sin (C)
Å andra sidan ger kosinosatsen oss dessa tre likheter för vilken triangel ABC som helst:
tilltvå= btvå + ctvå -2bc * cos (A)
btvå= atvå + ctvå -2ac * cos (B)
ctvå= atvå + btvå -2ab * cos (C)
Dessa satser är också kända som sinuslagen respektive cosinuslagen..
En annan egenskap som vi kan ge av de akuta trianglarna är att två av dessa är lika om de uppfyller något av följande kriterier:
- Om de har alla tre lika sidor.
- Om de har en sida och två lika vinklar mot varandra.
- Om de har två lika sidor och en vinkel.
Vi kan klassificera akuta trianglar baserat på deras sidor. Dessa kan vara:
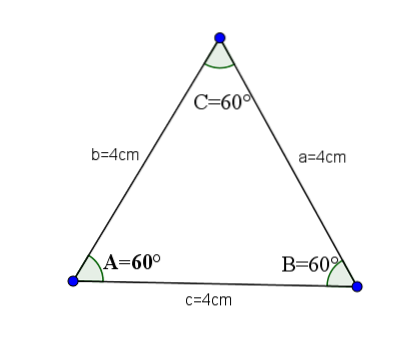
De är de akuta trianglarna som har alla sidor lika och därför har alla deras inre vinklar samma värde, vilket är A = B = C = 60 ° grader.
Som ett exempel, låt oss ta följande triangel, vars sidor a, b och c har ett värde på 4.
Dessa trianglar har, förutom att de har akuta inre vinklar, karaktäristiken att ha två av sina lika sidor och den tredje, som i allmänhet tas som bas, annorlunda.
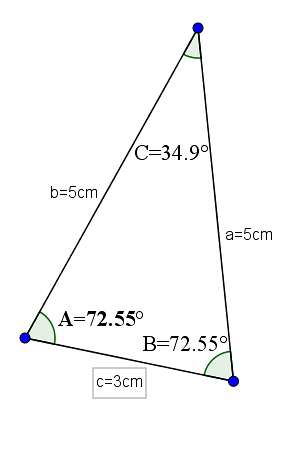
Ett exempel på denna typ av triangel kan vara en vars bas är 3 och dess andra två sidor har ett värde på 5. Med dessa mätningar skulle den ha motsatta vinklar till lika sidor med värdet 72,55 ° och motsatt vinkel av basen skulle vara 34,9 °.
Det här är trianglarna som alla har olika sidor två och två. Därför är alla dess vinklar, förutom att de är mindre än 90 °, olika från två till två.
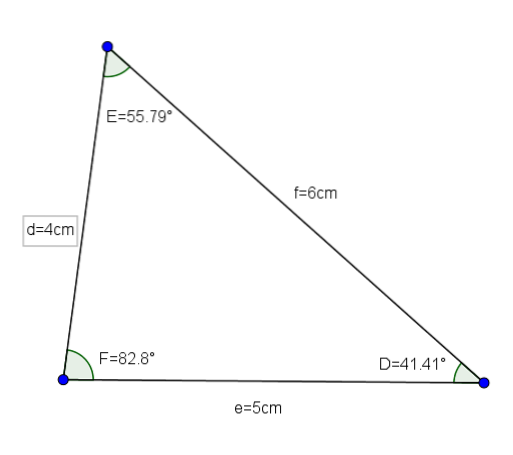
Triangeln DEF (vars mått är d = 4, e = 5 och f = 6 och dess vinklar är D = 41,41 °, E = 55,79 ° och F = 82,8 °) är ett bra exempel på en akut triangel skalen.
Som vi sa tidigare, för att lösa problem med akuta trianglar är det nödvändigt att använda sinus- och cosinussatserna.
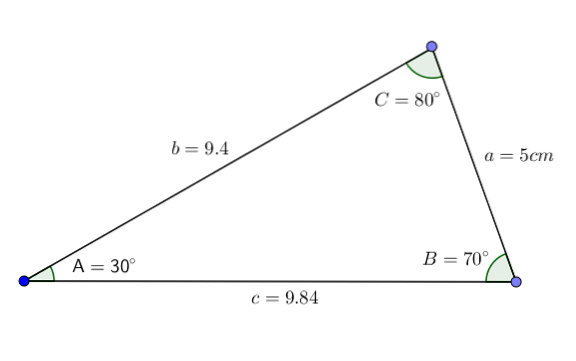
Med tanke på en triangel ABC med vinklarna A = 30 °, B = 70 ° och sidan a = 5 cm, vill vi veta värdet på vinkeln C och sidorna b och c.
Det första vi gör är att använda det faktum att summan av de inre vinklarna i en triangel är 180 °, för att erhålla värdet på vinkel C.
180 ° = A + B + C = 30 ° + 70 ° + C = 100 ° + C
Vi rensar C och vi sitter kvar med:
C = 180 ° - 100 ° = 80 °
Eftersom vi redan känner till de tre vinklarna och den ena sidan kan vi använda sinussatsen för att bestämma värdet på de återstående sidorna. Med satsen har vi:
a / sin (A) = b / sin (B) och a / sin (A) = c / (sin (C)
Vi isolerar b från ekvationen och vi sitter kvar med:
b = (a * sin (B)) / sin (A) ≈ (5 * 0,940) / (0,5) ≈ 9,4
Nu behöver vi bara beräkna värdet på c. Vi fortsätter på samma sätt som i föregående fall:
c = (a * sin (C)) / sin (A) ≈ (5 * 0,984) / (0,5) ≈ 9,84
Således får vi alla triangeldata. Som vi kan se faller denna triangel in i kategorin av scalene akut triangel.
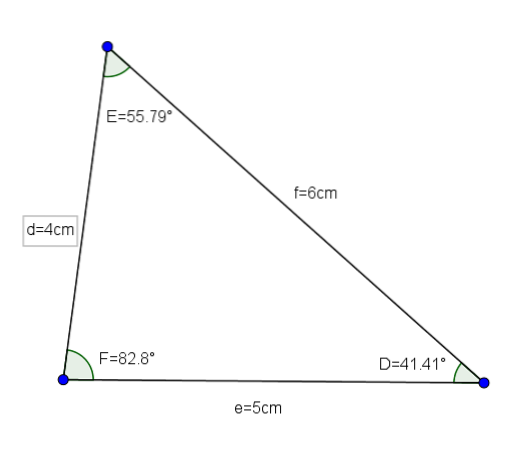
Med tanke på en triangel DEF med sidorna d = 4 cm, e = 5 cm och f = 6 cm, vill vi veta värdet på vinklarna i nämnda triangel.
I det här fallet kommer vi att använda kosinuslagen, som säger oss att:
dtvå= etvå + Ftvå - 2efcos (D)
Från denna ekvation kan vi lösa för cos (D), vilket ger oss som ett resultat:
Cos (D) = ((4)två - (5)två -(6)två) / (- 2 * 5 * 6) = 0,75
Därför har vi D≈ 41,41 °
Nu använder vi senosatsen vi har följande ekvation:
d / (sin (D) = e / (sin (E)
Att lösa för synd (E) har vi:
sin (E) = e * sin (D) / d = (5 * 0,66) / 4 ~ 0,827
Därför har vi E≈55,79 °
Slutligen, med hjälp av att summan av de inre vinklarna i en triangel är 180 °, har vi det F≈82.8 °.
Ingen har kommenterat den här artikeln än.