
Resulterande vektorberäkning, exempel, övningar
De resulterande vektor är den som erhålls med hjälp av en operation med vektorer vars resultat också är en vektor. Normalt är denna operation summan av två eller flera vektorer, med hjälp av vilka en vektor erhålls vars effekt är ekvivalent.
På detta sätt erhålles vektorer såsom den resulterande hastigheten, accelerationen eller kraften. Till exempel när flera krafter verkar på en kropp F1, Ftvå, F3,.... vektorsumman av alla dessa krafter är ekvivalent med nettokraften (den resulterande), som matematiskt uttrycks enligt följande:
F1 + Ftvå + F3 +... = FR eller FN

Den resulterande vektorn, oavsett om det är krafter eller någon annan vektorstorlek, hittas genom att tillämpa reglerna för vektortillsats. Eftersom vektorerna har riktning och känsla utöver det numeriska värdet räcker det inte att lägga till modulerna för att få den resulterande vektorn.
Detta gäller bara i fallet där de inblandade vektorerna är i samma riktning (se exempel). Annars är det nödvändigt att använda vektorsummetoder, som, beroende på fallet, kan vara geometriska eller analytiska..
Artikelindex
- 1 Exempel
- 1.1 Geometriska metoder för att lägga till två vektorer
- 2 övningar
- 2.1-Övning 1
- 2.2 Övning 2
- 3 Referenser
Exempel
De geometriska metoderna för att hitta den resulterande vektorn är polygonalmetoden och parallellogrammetoden.
När det gäller analytiska metoder finns det komponentmetoden, med vilken vektorn som härrör från vilket vektorsystem som helst kan hittas, förutsatt att vi har dess kartesiska komponenter..
Geometriska metoder för att lägga till två vektorer
Antag att vektorerna eller Y v (Vi betecknar dem med fet stil för att skilja dem från skalärerna). I figur 2a) har vi dem placerade på planet. I figur 2 b) har den överförts till vektorn v på ett sådant sätt att dess ursprung sammanfaller med slutet av eller. Den resulterande vektorn går från ursprunget till den första (eller) till toppen av den sista (v):
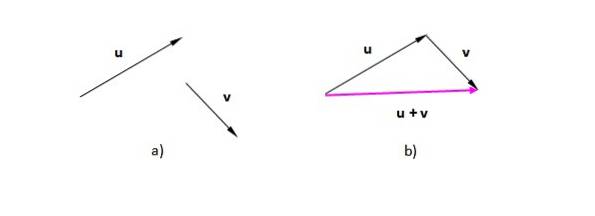
Den resulterande figuren i detta fall är en triangel (en triangel är en 3-sidig polygon). Om vi har två vektorer i samma riktning är proceduren densamma: placera en av vektorerna efter den andra och rita en som går från den första eller svansen på den första till spetsen eller slutet på den sista.
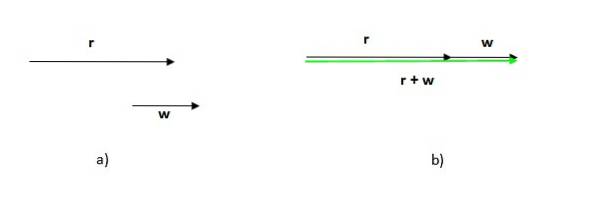
Observera att den ordning som denna procedur görs inte spelar någon roll, eftersom summan av vektorer är kommutativ.
Observera också att i detta fall modul (längden eller storleken) på den resulterande vektorn är summan av modulerna för de tillagda vektorerna, till skillnad från det föregående fallet, där modulen för den resulterande vektorn är mindre än summan av deltagarnas moduler.
Parallelogrammetod
Denna metod är mycket lämplig när du behöver lägga till två vektorer vars ursprungspunkter sammanfaller, till exempel med ursprunget till ett x-y-koordinatsystem. Antag att detta är fallet för våra vektorer eller Y v (figur 3a):
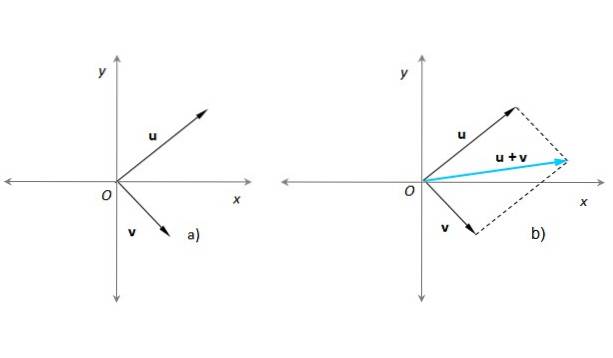
I figur 3b har ett parallellogram konstruerats med hjälp av prickade linjer parallellt med eller redan v. Den resulterande vektorn har sitt ursprung vid O och dess slut vid den punkt där de streckade linjerna skär varandra. Denna procedur är helt likvärdig med den som beskrivs i föregående avsnitt..
Träning
-Övning 1
Med tanke på följande vektorer, hitta den resulterande vektorn med hjälp av traversmetoden.
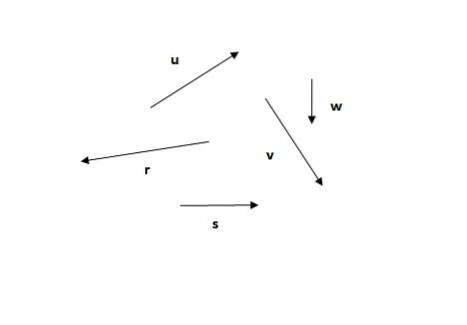
Lösning
Traversmetoden är den första av de metoder som ses. Kom ihåg att summan av vektorer är kommutativ (ordningen på tilläggen ändrar inte summan), så du kan börja med någon av vektorerna, till exempel eller (figur 5a) eller r (figur 5b):
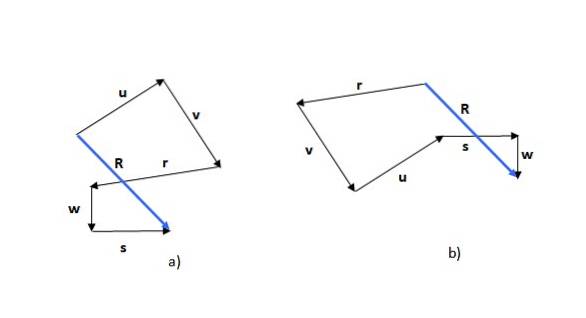
Den erhållna figuren är en polygon och den resulterande vektorn (i blått) kallas R. Om du börjar med en annan vektor kan formen som bildas vara annorlunda, vilket kan ses i exemplet, men den resulterande vektorn är densamma.
Övning 2
I följande figur är det känt att modulerna för vektorerna eller Y v respektive är de u = 3 godtyckliga enheter och v = 1,8 godtyckliga enheter. Vinkeln som eller form med den positiva x-axeln är 45º, medan v den bildar 60º med y-axeln, som visas i figuren. Hitta den resulterande vektorn, storleken och riktningen.
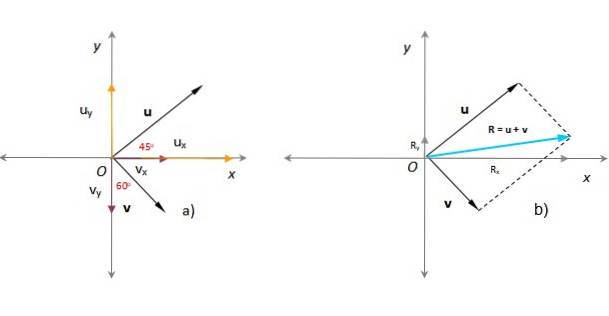
Lösning
I föregående avsnitt hittades den resulterande vektorn genom att använda parallellogrammetoden (i turkos i figuren).
Ett enkelt sätt att hitta den resulterande vektorn analytiskt är att uttrycka tillsatsvektorerna i termer av deras kartesiska komponenter, vilket är lätt när modul och vinkel är känd, såsom vektorerna i detta exempel:
ellerx = u. cos 45º = 3 x cos 45º = 2.12; ellerY = u. sin 45º = 3x sin 45º = 2.12
vx = v. sin 60º = 1,8 x sin 60º = 1,56; vY = -v. cos 60º = -1,8 x cos 60º = - 0,9
Vektorer eller Y v de är vektorer som tillhör planet och har därför två komponenter vardera. Vektor u finns i den första kvadranten och dess komponenter är positiva, medan vektorn v är i den fjärde kvadranten; dess x-komponent är positiv, men dess projektion på den vertikala axeln faller på den negativa y-axeln.
Beräkning av de kartesiska komponenterna i den resulterande vektorn
Den resulterande vektorn hittas genom att addera algebraiskt respektive x- och y-komponenter för att erhålla deras kartesiska komponenter:
Rx = 2,12 + 1,56 = 3,68
RY = 2,12 + (-0,9) = 1,22
När de kartesiska komponenterna har specificerats är vektorn helt känd. Den resulterande vektorn kan uttryckas med notationen inom hakparenteser (tandställning):
R = < 3.68; 1.22> godtyckliga enheter
Beteckningen med hakparenteser används för att skilja en vektor från en punkt i planet (eller i rymden). Ett annat sätt att uttrycka den resulterande vektorn analytiskt är att använda enhetsvektorerna i och j i planet (i, j Y k i rymden):
R = 3,68 i + 1.22 j godtyckliga enheter
Eftersom båda komponenterna i den resulterande vektorn är positiva, är vektorn R tillhör den första kvadranten, som redan sett grafiskt tidigare.
Storlek och riktning för den resulterande vektorn
Genom att känna till de kartesiska komponenterna beräknas storleken på R genom Pythagoras sats, eftersom den resulterande vektorn R, tillsammans med dess R-komponenterx och RY bilda en rätt triangel:
Storlek eller modul: R = (3.68två + 1.22två)½ = 3,88
Riktning q med den positiva x-axeln som referens: q = arctan (RY / Rx) = arctg (1,22 / 3,68) = 18,3 º
Referenser
- Lägga till vektorer och regler. Hämtad från: newt.phys.unsw.edu.au
- Figueroa, D.-serien: Fysik för vetenskap och teknik. Volym 1. Kinematik. 31-68.
- Fysisk. Modul 8: Vektorer. Återställd från: frtl.utn.edu.ar
- Hibbeler, R. 2006. Mekanik för ingenjörer. Statisk. 6: e upplagan. Continental Publishing Company. 15-53.
- Vector Addition Calculator. Hämtad från: www.1728.org


Ingen har kommenterat den här artikeln än.