
Collinear Vectors System och exempel
De kollinära vektorer De är en av de tre typerna av befintliga vektorer. Dessa är de vektorerna som är i samma riktning eller handlingslinje. Detta betyder följande: två eller flera vektorer kommer att vara kollinära om de är ordnade i linjer som är parallella med varandra.
En vektor definieras som en mängd som appliceras på en kropp och kännetecknas av att ha en riktning, en känsla och en skala. Vektorer finns i planet eller i rymden och kan vara av olika typer: kollinära vektorer, samtidiga vektorer och parallella vektorer.

Artikelindex
- 1 Collinear-vektorer
- 2 funktioner
- 2.1 Exempel 1
- 2.2 Exempel 2
- 2.3 Exempel 1
- 3 Collinear vektorsystem
- 3.1 Kollinära vektorer med motsatta riktningar
- 3.2 Kollinära vektorer med samma riktning
- 3.3 Kollinära vektorer med lika storleksordning och motsatta riktningar
- 4 Skillnad mellan kollinära och samtidiga vektorer
- 5 Referenser
Kollinära vektorer
Vektorer är kollinära om handlingslinjen för en är exakt samma handlingslinje för alla andra vektorer, oavsett storlek och riktning på var och en av vektorerna.
Vektorer används som representationer i olika områden som matematik, fysik, algebra och även i geometri, där vektorer endast är kollinära när deras riktning är densamma, oavsett om deras känsla inte är det..
Egenskaper
- Två eller flera vektorer är kollinära om förhållandet mellan koordinaterna är lika.
Exempel 1
Vi har vektorerna m = m_x; m_y och n = n_x; n_y. Dessa är kollinära om:
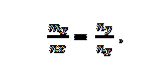
Exempel 2
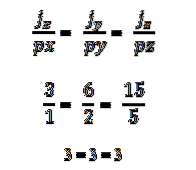
- Två eller flera vektorer är kollinära om vektorprodukten eller multiplikationen är lika med noll (0). Detta beror på att i vektorsystemet kännetecknas varje vektor av sina respektive koordinater, och om dessa är proportionella mot varandra kommer vektorerna att vara kollinära. Detta uttrycks på följande sätt:
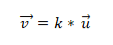
Exempel 1
Vi har vektorerna a = (10, 5) och b = (6, 3). För att avgöra om de är kollinära tillämpas determinantteorin som fastställer likformigheten mellan korsprodukterna. Således måste du:
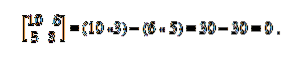
Collinear vektorsystem
Kollinära vektorer representeras grafiskt med riktning och känsla för dessa - med hänsyn till att de måste passera genom applikationspunkten - och modulen, som är en viss skala eller längd..
Systemet med kollinära vektorer bildas när två eller flera vektorer verkar på ett föremål eller kropp, som representerar en kraft och verkar i samma riktning..
Till exempel, om två kollinära krafter appliceras på en kropp beror resultatet av dessa bara på den riktning de verkar i. Det finns tre fall, som är:
Kollinära vektorer med motsatta riktningar
Resultatet av två kollinära vektorer är lika med summan av dessa:
R = ∑ F = F1 + Ftvå.
Exempel
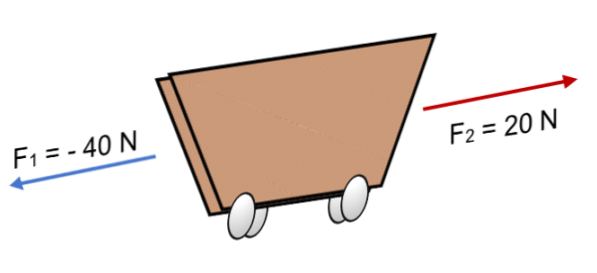
Om två krafter F verkar på en vagn1 = 40 N och F.två = 20 N i motsatt riktning (som bilden visar) är resultatet:
R = ∑ F = (- 40 N) + 20N.
R = - 20 N..
Kollinära vektorer med samma mening
Storleken på den resulterande kraften kommer att vara lika med summan av de kollinära vektorerna:
R = ∑ F = F1 + Ftvå.
Exempel
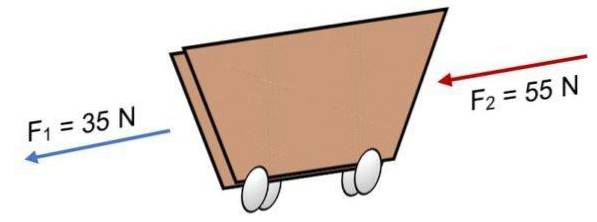
Om två krafter F verkar på en vagn1 = 35 N och F.två = 55 N i samma riktning (som visas på bilden), resultatet är:
R = ∑ F = 35 N + 55N.
R = 90 N..
Det positiva resultatet indikerar att de kollinära vektorerna verkar till vänster.
Kollinära vektorer med samma storlek och motsatta riktningar
Resultatet av de två kollinära vektorerna kommer att vara lika med summan av de kollinära vektorerna:
R = ∑ F = F1 + Ftvå.
Eftersom krafterna har samma storlek men i motsatt riktning - det vill säga att den ena kommer att vara positiv och den andra negativa - när de två krafterna läggs till kommer den resulterande att vara lika med noll..
Exempel
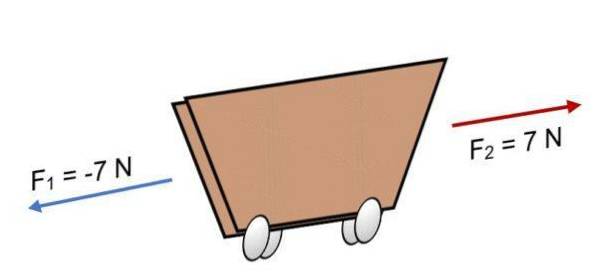
Om två krafter F verkar på en vagn1 = -7 N och Ftvå = 7 N, som har samma storlek men i motsatt riktning (som visas på bilden) är resultatet:
R = ∑ F = (-7 N) + 7N.
R = 0.
Eftersom resultatet är lika med 0 betyder det att vektorerna balanserar varandra och därför är kroppen i jämvikt eller i vila (den rör sig inte).
Skillnad mellan kollinära och samtidiga vektorer
Kollinära vektorer kännetecknas av att de har samma riktning i samma linje, eller för att de är parallella med en linje; det vill säga de är regissörvektorer med parallella linjer.
Samtidiga vektorer definieras eftersom de befinner sig i olika handlingslinjer som skär varandra vid en enda punkt..
Med andra ord har de samma utgångspunkt eller ankomst - oavsett modul, riktning eller riktning - som bildar en vinkel mellan dem..
Samtidiga vektorsystem löses med matematiska eller grafiska metoder, som är metoden parallellogram av krafter och metoden med krafter polygon. Genom dessa kommer värdet på en resulterande vektor att bestämmas, vilket indikerar i vilken riktning en kropp rör sig.
I grund och botten är den huvudsakliga skillnaden mellan kollinära och samtidiga vektorer handlingslinjen där de verkar: de kollinära verkar i samma linje, medan samtidiga i olika.
Det vill säga de kollinära vektorerna verkar i ett enda plan, "X" eller "Y"; och de samtidiga agerar i båda planen, från samma punkt.
Kollinära vektorer möts inte vid en punkt, som samtidiga vektorer gör, eftersom de är parallella med varandra.
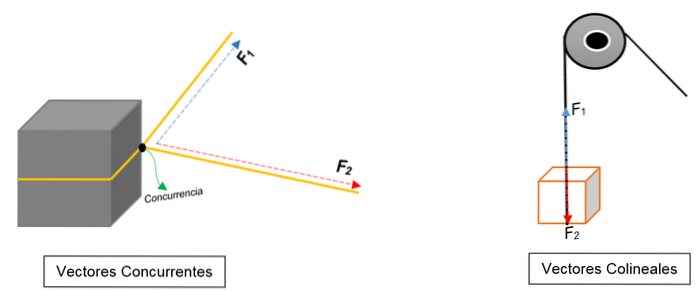
I den vänstra bilden kan du se ett block. Den är bunden med ett rep och knuten delar den i två; när det dras mot olika riktningar och med olika krafter kommer blocket att röra sig i samma riktning.
Två vektorer som överensstämmer vid en punkt (blocket) representeras, oavsett modul, riktning eller riktning.
Å andra sidan finns det i den högra bilden en remskiva som lyfter en låda. Repet representerar handlingslinjen; när den dras, verkar två krafter (vektorer) på den: en spänningskraft (när blocket höjs) och en annan kraft som utövar vikten på blocket. Båda har samma riktning men i motsatta riktningar; de överensstämmer inte vid en tidpunkt.
Referenser
- Estalella, J. J. (1988). Vektoranalys. Volym 1.
- Gupta, A. (s.f.). Tata McGraw-Hill Education.
- Jin Ho Kwak, S. H. (2015). Linjär algebra. Springer Science & Business Media.
- Montiel, H. P. (2000). Fysik 1 för teknologiska studenter. Grupo Ledare Patria.
- Santiago Burbano de Ercilla, C. G. (2003). Allmän fysik. Ledare Tebar.
- Sinha, K. (s.f.). A Math Book of Mathematics XII Vol. 2. Rastogi Publications.

Ingen har kommenterat den här artikeln än.