
Mesh-analysbegrepp, metoder, exempel
De nätanalys är en teknik som används för att lösa platta elektriska kretsar. Denna procedur kan också visas i litteraturen under metodnamnen på kretsströmmar eller metod för nätströmmar (eller slinga).
Grunden för denna och andra metoder för analys av elektriska kretsar ligger i Kirchhoffs lagar och Ohms lag. Kirchhoffs lagar är i sin tur uttryck för två mycket viktiga principer för bevarande i fysik för isolerade system: både den elektriska laddningen och energin bevaras..

Å ena sidan är den elektriska laddningen relaterad till strömmen, vilket är laddningen i rörelse, medan i en krets är energin kopplad till spänningen, vilket är den agent som ansvarar för att göra det arbete som krävs för att hålla laddningen i rörelse..
Dessa lagar, som tillämpas på en platt krets, genererar en uppsättning samtidiga ekvationer som måste lösas för att erhålla ström- eller spänningsvärdena..
Systemet med ekvationer kan lösas med välkända analytiska tekniker, såsom cramer regel, som kräver beräkning av determinanter för att erhålla systemets lösning.
Beroende på antalet ekvationer löses de med en vetenskaplig kalkylator eller någon matematisk programvara. På nätet finns det också många alternativ.
Artikelindex
- 1 Viktiga villkor
- 2 Metoder
- 2.1 - Steg för att tillämpa nätanalys
- 3 Lösta övningar
- 3.1 - Exempel 1
- 3.2 - Exempel 2
- 4 Referenser
Viktiga villkor
Innan vi förklarar hur det fungerar, börjar vi med att definiera dessa termer:
Gren: sektion som innehåller ett kretselement.
Nod: punkt som förbinder två eller flera grenar.
Band: är vilken som helst sluten del av en krets som börjar och slutar vid samma nod.
Maska: slinga som inte innehåller någon annan slinga inuti (väsentligt nät).
Metoder
Meshanalys är en allmän metod som används för att lösa kretsar vars element är kopplade i serie, parallellt eller på ett blandat sätt, det vill säga när anslutningstypen inte skiljer sig tydligt. Kretsen måste vara plan, eller åtminstone måste den kunna ritas om som sådan.
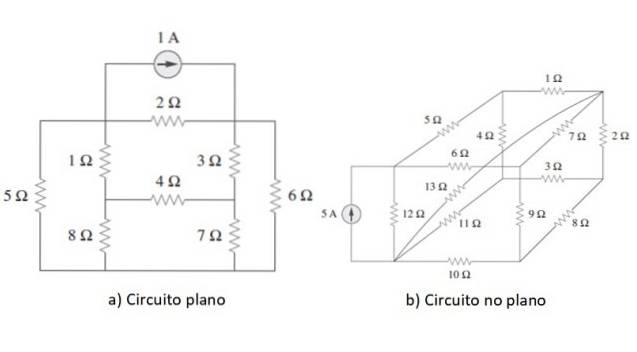
Ett exempel på varje typ av krets visas i figuren ovan. När punkten har klargjorts, för att börja, kommer vi att använda metoden på en enkel krets som ett exempel i nästa avsnitt, men först kommer vi att kort granska lagarna i Ohm och Kirchhoff.
Ohms lag: vara V spänningen, R motstånd e Jag strömmen hos det ohmiska resistiva elementet, i vilket spänningen och strömmen är direkt proportionella, varvid motståndet är proportionalitetskonstanten:
V = I.R
Kirchhoff's Voltage Law (LKV): I alla stängda vägar som bara färdas i en riktning är den algebraiska summan av spänningarna noll. Detta inkluderar spänningar på grund av källor, motstånd, induktorer eller kondensatorer: ∑ E = ∑ Ri. Jag
Kirchhoffs nuvarande lag (LKC): vid vilken nod som helst är den algebraiska summan av strömmarna noll, med hänsyn till att de inkommande strömmarna tilldelas ett tecken och de som lämnar en annan. På detta sätt: ∑ I = 0.
Med nätströmmetoden är det inte nödvändigt att tillämpa Kirchhoffs nuvarande lag, vilket resulterar i färre ekvationer att lösa.
- Steg för att tillämpa nätanalys
Vi börjar med att förklara metoden för en 2-mesh krets. Proceduren kan sedan utökas för större kretsar.
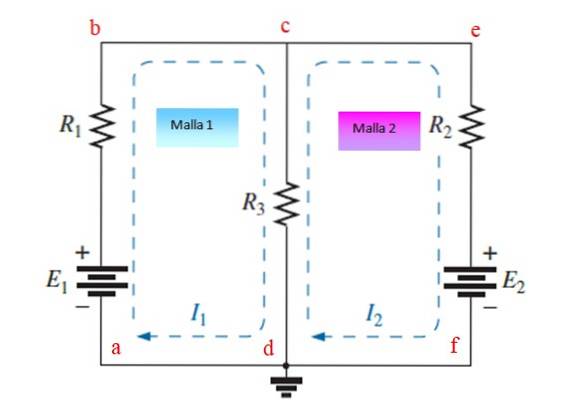
Steg 1
Tilldela och rita oberoende strömmar till varje nät, i detta exempel är de Jag1 och Jagtvå. De kan dras medurs eller moturs.
Steg 2
Tillämpa Kirchhoffs lag om spänningar (LTK) och Ohms lag på varje nät. Potentiella droppar tilldelas ett tecken (-) medan höjningar tilldelas ett tecken (+).
Mesh abcda
Med utgångspunkt från punkt a och följer strömens riktning, hittar vi en potentiell ökning av batteriet E1 (+), sedan en minskning av R1 (-) och sedan ytterligare en droppe i R3 (-).
Samtidigt har motståndet R3 korsas också av nuvarande jagtvå, men i motsatt riktning representerar den därför en ökning (+). Den första ekvationen ser ut så här:
OCH1-R1.Jag1 -R3.Jag1 + R3.Jagtvå = 0
Sedan tas det med i beräkningen och termerna grupperas om:
- (R1+R3) Jag1 +R3Jagtvå = -E1 (Ekvation 1)
Cefdc-nät
Börjar från punkten och och efter strömens riktning finns en potentiell nedgång i Rtvå (-), en ny drop in OCHtvå, eftersom strömmen kommer in genom + polen på batteriet och äntligen ytterligare ett fall R3 (-), samtidigt strömmen Jag1 korsar R3 i motsatt riktning (+).
Den andra ekvationen, med de angivna tecknen, ser ut så här:
- Rtvå Jagtvå - OCHtvå -R3 Jagtvå +R3 Jag1= 0
R3Jag1 - (Rtvå +R3) Jagtvå = Etvå (Ekvation 2)
Observera att det finns två ekvationer med de två okända I1 och jagtvå.
Steg 3
Systemet av ekvationer som sålunda bildas löses sedan.
Lösta övningar
Till att börja med är det viktigt att överväga följande:
-Slingströmmar eller nätströmmar kan tilldelas en godtycklig adress.
-Varje väsentligt nät - eller "fönster" - som kretsen har måste tilldelas en ström.
-Nätströmmar betecknas med en stor bokstav för att skilja dem från strömmar som cirkulerar genom grenar, även om strömmen som cirkulerar genom en gren i vissa fall kan vara densamma som nätets.
- Exempel 1
Hitta strömmarna som strömmar genom varje motstånd i kretsen i figur 3, om elementen har följande värden:
R1 = 20 Ω; Rtvå = 30 Ω; R3 = 10 Ω; OCH1 = 12 V; OCHtvå = 18 V
Lösning
Först är det nödvändigt att tilldela nätströmmarna I1 och jagtvå och ta systemet med ekvationer som dras i föregående avsnitt, ersätt sedan värdena i uttalandet:
- (R1+R3) Jag1 +R3Jagtvå = -E1 (Ekvation 1)
R3Jag1 - (Rtvå +R3) Jagtvå = Etvå (Ekvation 2)
-
-(20 + 30) Jag1 + 10Itvå = -12
10I1 - (30 +10) Itvå = 18
--
-femtioJag1 + 10Itvå = -12
10I1 - 40 Itvå = 18
Eftersom det är ett 2 x 2-system av ekvationer kan det enkelt lösas genom reduktion, multiplicera den andra ekvationen med 5 för att eliminera det okända Jag1:
-femtioJag1 + 10 jagtvå = -12
50I1 - 200 Itvå = 90
-
-190 Itvå= 78
Jagtvå = - 78/180 A = - 0,41 A.
Omedelbart rensas strömmen Jag1 från någon av de ursprungliga ekvationerna:
Jag1 = (18 + 40 Itvå) / 10 = (18 + 40 x (-0,41)) / 10 = 0,16 A
Det negativa tecknet i strömmen Jagtvå betyder att strömmen i nät 2 cirkulerar i motsatt riktning mot den som dras.
Strömmarna i varje motstånd är som följer:
För motståndet R1 strömmen cirkulerar Jag1 = 0,16 A. i den mening som dras av motstånd Rtvå strömmen cirkulerar Jagtvå = 0,41 A. i motsatt riktning mot den som dras och av motståndet R3 cirkulera i3 = 0,16- (-0,41) A = 0,57 A. ner.
Systemlösning enligt Cramers metod
I matrisform kan systemet lösas enligt följande:
Steg 1: Beräkna Δ

Steg 2: Beräkna Δ1
Den första kolumnen ersätts av de oberoende termerna i ekvationssystemet, vilket bibehåller ordningen i vilket systemet ursprungligen föreslogs:

Steg 3: Beräkna I1
Jag1 = Δ1/ A = 300/1900 = 0,16 A
Steg 4: Beräkna Δtvå

Jagtvå = Δtvå/ A = -780/1900 = -0,41 A.
- Exempel 2
Bestäm strömmen och spänningarna genom varje motstånd i följande krets med nätströmmetoden:

Lösning
De tre nätströmmarna ritas, som visas i följande figur, i godtyckliga riktningar. Nu korsas maskorna med start från vilken punkt som helst:
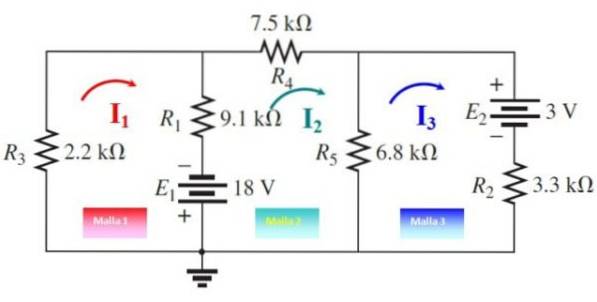
Mask 1
-9100.I1+18-2200.I1+9100.Itvå= 0
-11300 I1 + 9100.Itvå = -18
Mask 2
-(7500 + 6800 + 9100) .Itvå + 9100.I1+6800.I3-18 = 0
9100.I1 - 23400.Itvå + 6800.I3 = 18
Mask 3
-(6800 + 3300) I3 + 6800.Itvå - 3 = 0
6800.Itvå - 10100.I3 = 3
System av ekvationer
-11300 I1 + 9100.Itvå + 0.I3= -18
9100.I1 - 23400.Itvå + 6800.I3 = 18
0.I1 + 6800.Itvå - 10100.I3 = 3
Även om siffrorna är stora kan det lösas snabbt med hjälp av en vetenskaplig miniräknare. Kom ihåg att ekvationerna måste ordnas och lägg till nollor på de platser där det okända inte visas, som det visas här.
Nätströmmarna är:
Jag1 = 0,0012 A; Jagtvå = -0.00048 A; Jag3 = -0.00062 A.
Strömmar Jagtvå och Jag3 cirkulera i motsatt riktning mot den som visas i figuren, eftersom de visade sig vara negativa.
Tabell över strömmar och spänningar i varje motstånd
| Motstånd (Ω) | Ström (förstärkare) | Spänning = I.R (volt) |
|---|---|---|
| 9100 | Jag1 -Jagtvå = 0,0012 - (- 0,00048) = 0,00168 | 15.3 |
| 3300 | 0,00062 | 2,05 |
| 2200 | 0,0012 | 2.64 |
| 7500 | 0,00048 | 3,60 |
| 6800 | Jagtvå -Jag3= -0.00048 - (- 0.00062) = 0.00014 | 0,95 |
Cramers regellösning
Eftersom de är stora, är det bekvämt att använda vetenskaplig notation för att arbeta med dem direkt.
Beräkning av I1
De färgade pilarna i determinanten 3 x 3 anger hur man hittar de numeriska värdena genom att multiplicera de angivna värdena. Låt oss börja med att få de från den första fästet i determinanten Δ:
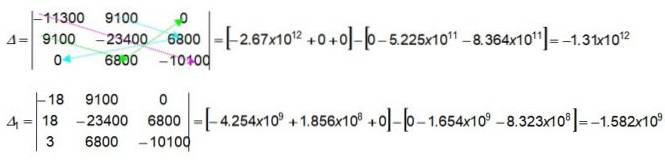
(-11300) x (-23400) x (-10100) = -2,67 x 1012
9100 x 0 x 0 = 0
9100 x 6800 x 0 = 0
Omedelbart får vi den andra fästet i samma determinant, som arbetas från vänster till höger (för den här fästet ritades inte de färgade pilarna i figuren). Vi uppmanar läsaren att verifiera det:
0 x (-23400) x 0 = 0
9100 x 9100 x (-10100) = -8,364 x 10elva
6800 x 6800 x (-11300) = -5,255 x 10elva
På samma sätt kan läsaren också kontrollera värdena för determinanten Δ1.
Viktig: mellan båda parenteserna finns alltid ett negativt tecken.
Slutligen får du strömmen Jag1 genom Jag1 = Δ1 / Δ
Jag1 = -1,582 x 109/-1,31 x 1012 = 0,0012 A.
Beräkning av Itvå
Proceduren kan upprepas för att beräkna Jagtvå, i detta fall att beräkna determinanten Δtvå den andra kolumnen i determinanten Δ ersätts med kolumnen med de oberoende termerna och dess värde hittas, enligt den förklarade proceduren.
Eftersom det är besvärligt på grund av det stora antalet, särskilt om du inte har en vetenskaplig räknare, är det enklaste att ersätta värdet på Jag1 redan beräknad, i följande ekvation och tydlig:
-11300 I1 + 9100.Itvå + 0.I3= -18 → 9100 Itvå= -18 + 11300 I1 → jagtvå = -0.00048 A.
Beräkning av I3
En gång med värdena för Jag1 och Jagtvå i handen, den av Jag3 hittas direkt genom substitution.
Referenser
- Alexander, C. 2006. Grundläggande för elektriska kretsar. 3: e. Utgåva. Mc Graw Hill.
- Boylestad, R. 2011. Introduktion till kretsanalys. 2da. Utgåva. Pearson.
- Figueroa, D. (2005). Serie: Fysik för vetenskap och teknik. Volym 5. Elektrisk interaktion. Redigerad av Douglas Figueroa (USB).
- García, L. 2014. Elektromagnetism. 2: a. Utgåva. Industrial University of Santander.
- Sears, Zemansky. 2016. Universitetsfysik med modern fysik. 14: e. Utg. Volym 2.



Ingen har kommenterat den här artikeln än.