A punktbelastning, I samband med elektromagnetism är det den elektriska laddningen med så små dimensioner att den kan betraktas som en punkt. Till exempel är elementära partiklar som har en elektrisk laddning, protonen och elektronen, så små att deras dimensioner kan utelämnas i många applikationer. Med tanke på att en laddning är punktorienterad blir jobbet med att beräkna dess interaktioner och förstå materiens elektriska egenskaper mycket lättare..
Elementära partiklar är inte de enda som kan vara punktladdningar. Så kan joniserade molekyler, de laddade sfärerna som Charles A. Coulomb (1736-1806) använde i sina experiment, och till och med jorden själv. Alla kan betraktas som punktladdningar, så länge vi ser dem på avstånd som är mycket större än objektets storlek..
Eftersom alla kroppar är gjorda av elementära partiklar är elektrisk laddning en inneboende egenskap hos materia, precis som massa. Du kan inte ha en elektron utan massa, och du kan inte heller ha någon laddning.
Artikelindex
Så vitt vi vet idag finns det två typer av elektrisk laddning: positiv och negativ. Elektroner har en negativ laddning, medan protoner har en positiv laddning..
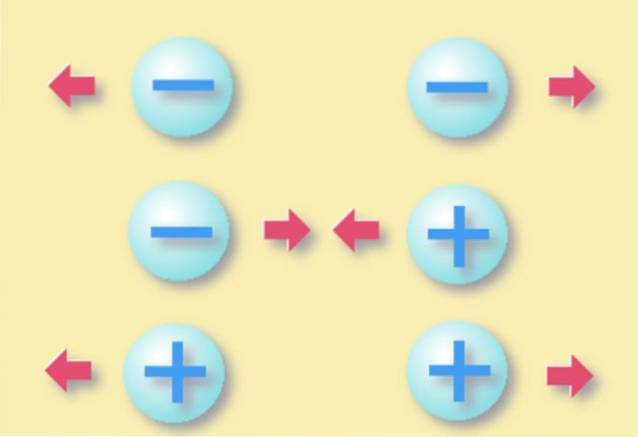
Avgifter av samma tecken stöter bort, medan motsatta tecken lockar. Detta gäller för alla typer av elektrisk laddning, antingen punktlig eller fördelad över ett objekt med mätbara dimensioner..
Dessutom verifierade noggranna experiment att laddningen av protonen och elektronens har exakt samma storlek..
En annan mycket viktig punkt att tänka på är att den elektriska laddningen kvantiseras. Hittills har inga isolerade elektriska laddningar av en storlek mindre än elektronens laddning hittats. De är alla multiplar av detta.
Slutligen sparas den elektriska laddningen. Med andra ord skapas eller förstörs inte elektrisk laddning, men den kan överföras från ett objekt till ett annat. På detta sätt, om systemet är isolerat, förblir den totala belastningen konstant..
Enheten för elektrisk laddning i International System of Units (SI) är Coulomb, förkortat med ett stort C, för att hedra Charles A. Coulomb (1736-1806), som upptäckte lagen som bär hans namn och beskriver samspelet mellan tvåpunktsavgifter. Vi kommer att prata om henne senare.
Elektronens elektriska laddning, som är den minsta möjliga som kan isoleras i naturen, har en styrka av:
och- = 1,6 x 10 -16 C
Coulomb är en ganska stor enhet, så submultiplen används ofta:
-1 milli C = 1 mC = 1 x 10-3 C
-1 mikro C = 1 μC = 1 x 10-6 C
-1 nano C = 1 nC = 1 x 10-9 C
Och som vi nämnde tidigare, tecknet på och- är negativ. Protonens laddning har exakt samma storlek, men med ett positivt tecken.
Tecknen är en fråga om konvention, det vill säga det finns två typer av elektricitet och det är nödvändigt att skilja dem, varför en tilldelas ett tecken (-) och det andra tecknet (+). Benjamin Franklin gjorde denna beteckning och förklarade också principen om bevarande av laddning..
Vid Franklins tid var atomens inre struktur fortfarande okänd, men Franklin hade observerat att en glasstav som gnuggades med siden blev elektriskt laddad och kallade denna typ av el positiv..
Alla objekt som lockades av nämnda elektricitet hade ett negativt tecken. Efter att elektronen upptäcktes observerades att den laddade glasstaven lockade dem, och så blev elektronladdningen negativ.
I slutet av 1700-talet tillbringade Coulomb, en fransk arméingenjör, lång tid på att studera materialens egenskaper, de krafter som verkar på balkarna och friktionskraften..
Men han minns bäst för lagen som bär hans namn och som beskriver samspelet mellan tvåpunkts elektriska laddningar.
Låt vara två elektriska laddningar Vad1 Y Vadtvå. Coulomb bestämde att kraften mellan dem, antingen attraktion eller avstötning, var direkt proportionell mot produkten av båda laddningarna och omvänt proportionell mot kvadratet på avståndet mellan dem..
Matematiskt:
F∝ vad1 . Vadtvå / rtvå
I denna ekvation, F representerar kraftens storlek och r är avståndet som skiljer laddningarna. Jämställdhet kräver en proportionalitetskonstant, som kallas elektrostatisk konstant och betecknas som koch.
Således:
F = k. Vad1 . Vadtvå / rtvå
Vidare fann Coulomb att styrkan riktades längs linjen som förbinder laddningarna. I så fall, ja r är enhetsvektorn längs denna linje, Coulombs lag som en vektor är:
Coulomb använde en anordning som heter torsionsbalans för dina experiment. Genom det var det möjligt att fastställa värdet på den elektrostatiska konstanten i:
koch = 8,99 x 109 N mtvå/ Ctvå ≈ 9,0 x 109 N mtvå/ Ctvå
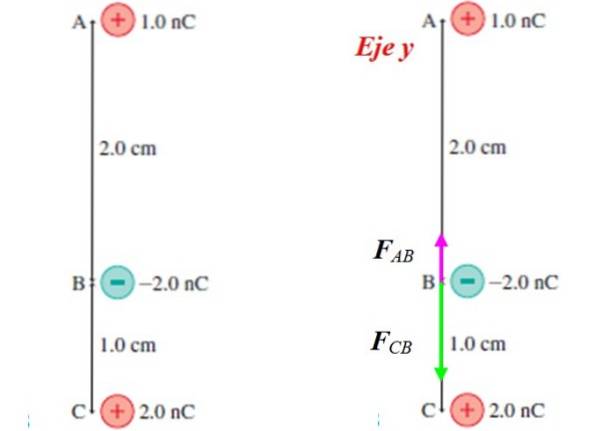
Därefter ser vi en ansökan. Det finns trepunktsavgifter qTILL, VadB och vadC som är i de positioner som anges i figur 2. Låt oss beräkna nettokraften på qB.
Lasten qTILL lockar den belastning somB, eftersom de har motsatta tecken. Samma kan sägas om qC. Det isolerade kroppsdiagrammet är i figur 2 till höger, där man observerar att båda krafterna är riktade längs den vertikala axeln eller y-axeln och har motsatta riktningar.
Nettokraften på laddningen qB det är:
FR = FAB + FCB (Princip för superposition)
Det återstår bara att ersätta de numeriska värdena, var noga med att skriva alla enheter i det internationella systemet (SI).
FAB = 9,0 x 109 x 1 x 10-9 x 2 x 10-9 / (2 x 10-två) två N (+Y) = 0,000045 (+Y) N
FCB = 9,0 x 109 x 2 x 10-9 x 2 x 10-9 / (1 x 10-två) två N (-Y) = 0,00036 (-Y) N
FR = FAB + FCB = 0,000045 (+Y) + 0,00036 (-YN = 0,000315 (-Y) N
Dessa två krafter har samma matematiska form. Naturligtvis skiljer de sig i värdet av proportionalitetskonstanten och genom att tyngdkraften arbetar med massor, medan elen fungerar med laddningar..
Men det viktiga är att båda beror på avståndets inversa kvadrat.
Det finns en unik typ av massa och den anses vara positiv, så tyngdkraften är alltid attraktiv, medan laddningar kan vara positiva eller negativa. Av denna anledning kan de elektriska krafterna vara attraktiva eller motbjudande, beroende på fallet..
Och vi har den här detalj som härrör från ovanstående: alla objekt i fritt fall har samma acceleration, så länge de är nära jordens yta..
Men om vi till exempel släpper en proton och en elektron nära ett laddat plan, kommer elektronen att ha en mycket större acceleration än protonen. Dessutom kommer accelerationerna att ha motsatta riktningar.
Slutligen kvantiseras den elektriska laddningen, precis som det sägs. Det betyder att vi kan hitta laddningar 2,3 eller 4 gånger elektronens - eller protonens - men aldrig 1,5 gånger denna laddning. Massorna, å andra sidan, är inte multiplar av någon unik massa.
I världen av subatomära partiklar överstiger den elektriska kraften den gravitationella i storlek. På makroskopiska skalor är dock tyngdkraften den dominerande. Var? På planetenivån, solsystemet, galaxen och mer.
Ingen har kommenterat den här artikeln än.