
Chi-kvadrat (χ²) fördelning, hur man beräknar det, exempel
Beviset Chi kvadrat eller chi-kvadrat (χtvå, där χ är den grekiska bokstaven som kallas "chi") används för att bestämma beteendet hos en viss variabel och även när du vill veta om två eller flera variabler är statistiskt oberoende.
För att kontrollera beteendet hos en variabel anropas testet som ska utföras chi kvadrat test av passform. För att ta reda på om två eller flera variabler är statistiskt oberoende, kallas testet chi kvadrat av självständighet, även kallad beredskap.
Dessa tester är en del av statistisk beslutsteori, där en population studeras och beslut fattas om den, analyserar ett eller flera prover som tagits från den. Detta kräver att man gör vissa antaganden om de variabler som kallas hypotes, vilket kan eller inte kan vara sant.
Det finns några tester för att kontrastera dessa antaganden och bestämma vilka som är giltiga, inom en viss tillitsmarginal, inklusive chi-kvadrat-testet, som kan användas för att jämföra två och fler populationer..
Som vi kommer se, lyfts vanligtvis två typer av hypoteser om någon populationsparameter i två prover: nullhypotesen, kallad Heller (proverna är oberoende), och den alternativa hypotesen, betecknad som H1, (proverna är korrelerade) vilket är motsatsen till det.
Artikelindex
- 1 När används chi-kvadrat-testet?
- 1.1 Villkor för att tillämpa det
- 2 Chi kvadratfördelning
- 2.1 Grader av frihet
- 2.2 Formulering av hypoteser
- 3 Hur beräknas chi-kvadratstatistiken?
- 3.1 Godtagningskriterier för Ho
- 4 Beräkningsexempel
- 5 Referenser
När används chi-kvadrat testet?
Chi-kvadrat-testet tillämpas på variabler som beskriver kvaliteter, såsom kön, civilstånd, blodgrupp, ögonfärg och preferenser av olika slag.
Testet är avsett när du vill:
-Kontrollera om en distribution är lämplig för att beskriva en variabel, som kallas godhet av passform. Med hjälp av chi-kvadrat-testet är det möjligt att veta om det finns signifikanta skillnader mellan den valda teoretiska fördelningen och den observerade frekvensfördelningen..
-Vet om två variabler X och Y är oberoende ur statistisk synvinkel. Detta kallas oberoende test.
Eftersom det tillämpas på kvalitativa eller kategoriska variabler används chi-kvadrat-testet i stor utsträckning inom samhällsvetenskap, ledning och medicin..
Villkor för att tillämpa det
Det finns två viktiga krav för att tillämpa det korrekt:
-Uppgifterna måste grupperas i frekvenser.
-Provet måste vara tillräckligt stort för att chi-kvadratfördelningen ska vara giltig, annars övervärderas dess värde och leder till att nollhypotesen avvisas när det inte borde vara fallet..
Den allmänna regeln är att om en frekvens med ett värde mindre än 5 visas i den grupperade datan används den inte. Om det finns mer än en frekvens mindre än 5, måste de kombineras till en för att erhålla en frekvens med ett numeriskt värde större än 5.
Chi kvadratfördelning
χtvå det är en kontinuerlig fördelning av sannolikheter. Egentligen finns det olika kurvor, beroende på en parameter k kallad grader av frihet av den slumpmässiga variabeln.
Dess egenskaper är:
-Arean under kurvan är lika med 1.
-Värdena för χtvå de är positiva.
-Fördelningen är asymmetrisk, det vill säga den har en bias.
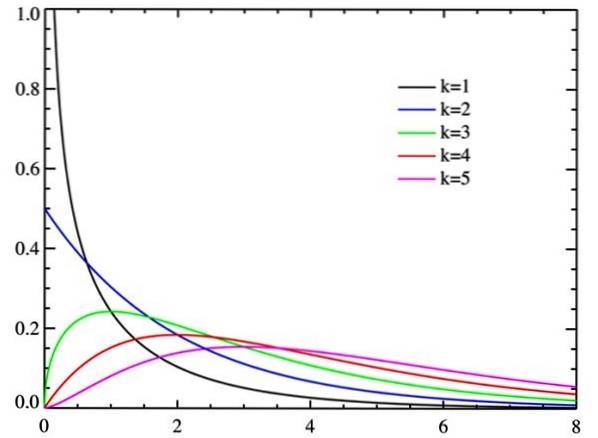
Grader av frihet
När frihetsgraderna ökar tenderar chi-kvadratfördelningen mot normalitet, vilket framgår av figuren.
För en given fördelning bestäms frihetsgraderna genom beredskapstabell, vilket är tabellen där de observerade frekvenserna för variablerna registreras.
Om ett bord har F rader och c kolumner, värdet på k det är:
k = (f - 1) ⋅ (c - 1)
Formulering av hypoteser
När chi-kvadrat-testet är lämpligt formuleras följande hypoteser:
-Heller: variabeln X har en sannolikhetsfördelning f (x) med de specifika parametrarna y1, Ytvå..., Ysid
-H1: X har en annan sannolikhetsfördelning.
Sannolikhetsfördelningen som antas i nollhypotesen kan till exempel vara den kända normalfördelningen och parametrarna är medelvärdet μ och standardavvikelsen σ.
Dessutom utvärderas nollhypotesen med en viss grad av betydelse, det vill säga ett mått på felet som skulle begås när man avvisar att det är sant.
Vanligtvis är denna nivå inställd på 1%, 5% eller 10% och ju lägre den är, desto mer tillförlitlig är testresultatet..
Och om det chi-kvadratiska testet av beredskap används, vilket, som vi har sagt, tjänar till att verifiera oberoende mellan två variabler X och Y, är hypoteserna:
-Heller: variablerna X och Y är oberoende.
-H1: X och Y är beroende.
Återigen är det nödvändigt att ange en nivå av betydelse för att veta måttet på felet när du fattar beslutet..
Hur beräknas chi-kvadratstatistiken?
Statistiken för chi-kvadrat beräknas enligt följande:

Summationen genomförs från första klass i = 1 till den sista, vilket är i = k.
Vad mer:
-Feller är en observerad frekvens (kommer från de erhållna uppgifterna).
-Foch är den förväntade eller teoretiska frekvensen (måste beräknas från data).
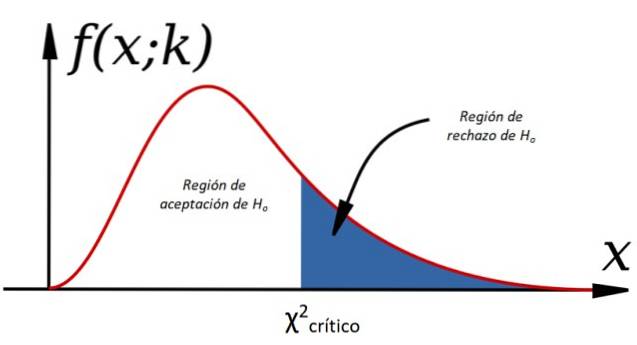
För att acceptera eller avvisa nollhypotesen beräknar vi χtvå för observerade data och jämfört med ett värde som kallas kritisk chi-kvadrat, vilket beror på frihetsgraderna k och nivån av betydelse a:
χtvåkritisk = χtvåk, a
Om vi till exempel vill utföra testet med en signifikansnivå på 1%, är α = 0,01, om det kommer att vara med 5% då α = 0,05 och så vidare. Vi definierar p, parametern för distributionen, som:
p = 1 - a
Dessa kritiska chi-kvadratvärden bestäms av tabeller som innehåller det kumulativa areavärdet. Till exempel, för k = 1, som representerar 1 frihetsgrad och α = 0,05, vilket är lika med p = 1- 0,05 = 0,95, värdet av χtvå är 3,841.

H acceptanskriteriereller
Kriteriet för att acceptera Heller det är:
-Ja χtvå < χtvåkritisk H accepteraseller, annars avvisas den (se figur 1).
Beräkningsexempel
I följande applikation kommer chi kvadrat testet att användas som ett test av oberoende.
Antag att forskarna vill veta om preferensen för svart kaffe är relaterad till personens kön och specificera svaret med en signifikansnivå på α = 0,05.
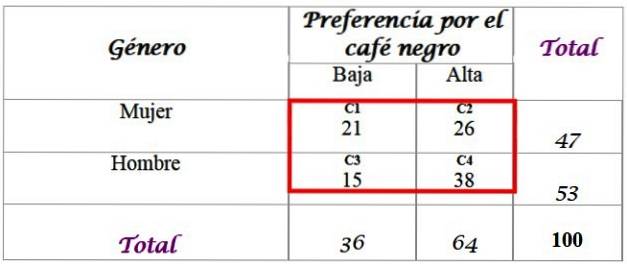
För detta finns ett urval på 100 personer som intervjuats och deras svar finns tillgängliga:
Steg 1
Fastställ hypoteserna:
-Heller: kön och preferens för svart kaffe är oberoende.
-H1: smaken för svart kaffe är relaterad till personens kön.
Steg 2
Beräkna de förväntade frekvenserna för distributionen, för vilka totalen som läggs till i sista raden och i den högra kolumnen i tabellen krävs. Varje cell i den röda rutan har ett förväntat värde Foch, som beräknas genom att multiplicera summan av din rad F med summan av din kolumn C, dividerat med summan av provet N:
Foch = (F x C) / N
Resultaten är följande för varje cell:
-C1: (36 x 47) / 100 = 16,92
-C2: (64 x 47) / 100 = 30,08
-C3: (36 x 53) / 100 = 19,08
-C4: (64 x 53) / 100 = 33,92
Steg 3
Därefter måste chi-kvadratstatistiken beräknas för denna fördelning enligt den givna formeln:

Steg 4
Bestäm χtvåkritisk, att veta att de inspelade uppgifterna finns i f = 2 rader och c = 2 kolumner, därför är antalet frihetsgrader:
k = (2-1) ⋅ (2-1) = 1.
Vilket innebär att vi måste titta i värdet på the i tabellen ovantvåk, a = χtvå1; 0,05 , vilket är:
χtvåkritisk = 3,841
Steg 5
Jämför värdena och bestäm:
χtvå = 2.9005
χtvåkritisk = 3,841
Sedan χtvå < χtvåkritisk nollhypotesen accepteras och man drar slutsatsen att preferensen för svart kaffe inte är kopplad till personens kön, med en signifikansnivå på 5%.
Referenser
- Chi Square Test för självständighet. Återställd från: saylordotorg.github.io.
- Med Wave. Statistik tillämpad på hälsovetenskap: chi-kvadrat-testet. Återställd från: medwave.cl.
- Sannolikheter och statistik. Chi-kvadrat test av godhet. Återställd från: probayestadistica.com.
- Triola, M. 2012. Elementär statistik. 11: e. Utgåva. Addison Wesley.
- UNAM. Chi fyrkantigt test. Återställd från: asesorias.cuautitlan2.unam.mx.



Ingen har kommenterat den här artikeln än.