
Konduktansformler, beräkning, exempel, övningar
De ledningsförmåga av en ledare definieras som den anläggning den har för att passera den elektriska strömmen. Det beror inte bara på materialet som används för tillverkningen utan också på dess geometri: längd och tvärsnittsarea.
Symbolen som används för konduktans är G, och det är det inversa av det elektriska motståndet R, en något mer välbekant mängd. SI International System-enheten för konduktans är den inversa av ohm, betecknad som Ω-1 och får namnet på siemens (S).

Andra termer som används i elektricitet som låter som liknar konduktans och är relaterade är ledningsförmåga och den körning, men de bör inte förväxlas. Den första av dessa termer är en inneboende egenskap hos det ämne som ledaren är tillverkad med och den andra beskriver strömmen av elektrisk laddning genom den..
För en elektrisk ledare med konstant tvärsnittsarea TILL, längd L och konduktivitet σ, konduktansen ges av:
G = σ.A / L
Ju högre konduktivitet, desto högre konduktans. Ju större tvärsnittsareal, desto lättare är det för ledaren att passera ström. Tvärtom, ju större längd L desto lägre konduktans, eftersom de nuvarande bärarna förlorar mer energi på längre vägar..
Artikelindex
- 1 Hur beräknas konduktans?
- 1.1 Ledningsenheter
- 2 Exempel
- 2.1 Konduktivitet och konduktans
- 2.2 Motstånd parallellt
- 3 Övningar
- 3.1 - Övning 1
- 3.2 - Övning 2
- 4 Referenser
Hur beräknas konduktans?
Konduktansen G för en ledare med konstant tvärsnittsarea beräknas enligt ekvationen ovan. Detta är viktigt, för om tvärsnittet inte är konstant måste du använda integralkalkylen för att hitta både motstånd och konduktans.
Eftersom det är motsatsens motsats kan konduktansen G beräknas med vetskap om att:
G = 1 / R
Faktum är att ledarens elektriska motstånd kan mätas direkt med en multimeter, en enhet som också mäter ström och spänning..
Ledningsenheter
Som anges i början är ledningsenheten i det internationella systemet Siemens (S). En ledare sägs ha en konduktans på 1 S om strömmen genom den ökar med 1 ampere för varje volt potentialdifferens.
Låt oss se hur det är möjligt genom Ohms lag, om det är skrivet i termer av konduktans:
V = I.R = I / G
Var V är spänningen eller potentialskillnaden mellan ändarna på ledaren e Jag strömintensitet. När det gäller dessa storlekar ser formeln ut så här:
G = I / V
Tidigare var enheten för konduktans mho (ohm skrivs bakåt) betecknas som Ʊ, vilket är en omvänd kapitalomega. Denna notation upphörde och ersattes av siemens till ära för den tyska ingenjören och uppfinnaren Ernst Von Siemens (1816-1892), pionjär inom telekommunikation, men båda är helt likvärdiga.
1 mho = 1 siemens = 1 A / V (ampere / volt)
I andra mätsystem statsiemens (statS) (i cgs eller centimeter-gram-sekund-systemet) och absiemens (abS) (elektromagnetiskt cgs-system) med "s" i slutet, utan att ange singular eller plural, eftersom de kommer från ett riktigt namn.
Vissa likvärdigheter
1 statS = 1.11265 x 10 -12 siemens
1 abS = 1 x 109 siemens
Exempel
Som nämnts tidigare är konduktansen omedelbart känd när man bestämmer det inversa eller ömsesidiga värdet med motstånd. På detta sätt motsvarar ett elektriskt motstånd på 100 ohm till exempel 0,01 siemen.
Här är ytterligare två exempel på användning av konduktans:
Konduktivitet och konduktans
De är olika termer, som redan angivits. Konduktivitet är en egenskap hos det ämne som ledaren är tillverkad med, medan ledningen är korrekt för ledaren.
Konduktivitet kan uttryckas i termer av G som:
σ = G. (L / A)
Här är en tabell med ledningsförmågan hos ofta använda ledande material:
bord 1. Konduktivitet, resistivitet och värmekoefficient hos vissa ledare. Referens temperatur: 20 ºC.
| Metall | σ x 106 (Eder) | ρ x 10-8 (Ω.m) | α ºC-1 |
|---|---|---|---|
| Silver | 62.9 | 1,59 | 0,0058 |
| Koppar | 56,5 | 1,77 | 0,0038 |
| Guld | 41,0 | 2,44 | 0,0034 |
| Aluminium | 35.4 | 2.82 | 0,0039 |
| Volfram | 18,0 | 5,60 | 0,0045 |
| Järn | 10,0 | 10,0 | 0,0050 |
Motstånd parallellt
När du har kretsar med motstånd parallellt är det ibland nödvändigt att få motsvarande motstånd. Att känna till värdet på motsvarande motstånd gör det möjligt att ersätta ett enda värde för uppsättningen motstånd.
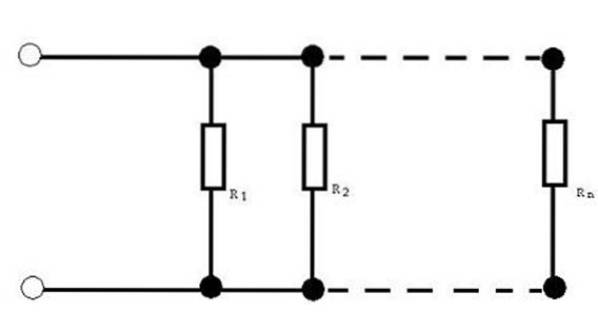
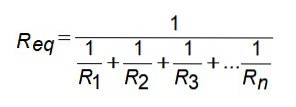
För denna motståndskonfiguration ges motsvarande motstånd av:
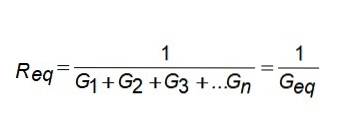
Gekv = G1 + Gtvå + G3 +... Gn
Det vill säga motsvarande konduktans är summan av konduktanserna. Om du vill veta motsvarande motstånd, helt enkelt invertera resultatet.
Träning
- Övning 1
a) Skriv Ohms lag med avseende på konduktans.
b) Hitta konduktansen för en volframtråd 5,4 cm lång och 0,15 mm i diameter.
c) Nu passerar en ström på 1,5 A genom ledningen. Vad är den potentiella skillnaden mellan ändarna på denna ledare?
Lösning till
Från föregående avsnitt måste du:
V = I / G
G = σ.A / L
Att ersätta det senare i det första ser det ut så här:
V = I /(σ.A/L) = I.L / σ.A
Var:
-Jag är strömens intensitet.
-L är ledarens längd.
-σ är konduktiviteten.
-A är tvärsnittsområdet.
Lösning b
För att beräkna konduktansen för denna volframtråd krävs dess konduktivitet, vilket finns i tabell 1:
σ = 18 x 106 Eder
L = 5,4 cm = 5,4 x 10-två m
D = 0,15 mm = 0,15 x 10-3 m
A = π.Dtvå / 4 = π. (0,15 x 10-3 m)två / 4 = 1,77 x 10-8 mtvå
Att ersätta ekvationen har vi:
G = σ.A / L = 18 x 106 Ja. 1,77 x 10-8 mtvå / 0,15 x 10-3 m = 2120,6 S.
Lösning c
V = I / G = 1,5 A / 2120,6 S = 0,71 mV.
- Övning 2
Hitta motsvarande motstånd i följande krets och veta att jageller = 2 A, beräkna ix och strömmen som försvinner av kretsen:
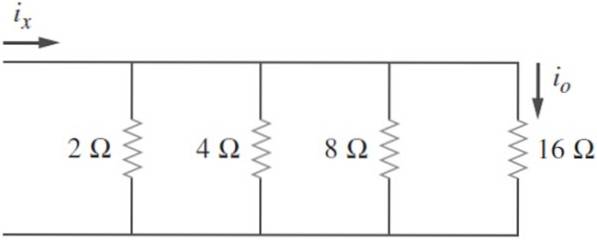
Lösning
Motstånd listas: R1= 2 Ω; Rtvå= 4 Ω; R3= 8 Ω; R4= 16 Ω
Därefter beräknas konduktansen i båda fallen: G1 = 0,5 Ʊ; Gtvå = 0,25 "; G3 = 0,125 °; G4 = 0,0625 Ʊ
Och slutligen läggs de till som angivits tidigare för att hitta motsvarande konduktans:
Gekv = G1 + Gtvå + G3 +... Gn = 0,5 "+ 0,25" + 0,125 "+ 0,0625" = 0,9375 "
Därför Rekv = 1,07 Ω.
Spänningen över R4 är V4 = ieller. R4 = 2 A. 16 Ω = 32 V, och det är detsamma för alla motstånd, eftersom de är anslutna parallellt. Då är det möjligt att hitta de strömmar som flyter genom varje motstånd:
-i1 = V1 / R1 = 32 V / 2 Ω = 16 A.
-itvå = Vtvå / Rtvå = 32 V / 4 Ω = 8 A.
-i3 = V3 / R3 = 32 V / 8 Ω = 4 A.
-ix = i1 + itvå + i3 + ieller = 16 + 8 + 4 + 2 A = 30 A.
Slutligen är den försvunna kraften P:
P = (ix)två. Rekv = 30 A x 1,07 Ω = 32,1 W
Referenser
- Alexander, C. 2006. Grundläggande för elektriska kretsar. 3: e. Utgåva. Mcgraw hill.
- Omvandling megaampere / millivolt till absiemens Calculator. Återställd från: pinkbird.org.
- García, L. 2014. Elektromagnetism. 2: a. Utgåva. Industrial University of Santander. Colombia.
- Knight, R. 2017. Physics for Scientists and Engineering: a Strategy Approach. Pearson.
- Roller, D. 1990. Fysik. Elektricitet, magnetism och optik. Volym II. Redaktionellt Reverté.
- Wikipedia. Elektrisk ledning. Återställd från: es.wikipedia.org.
- Wikipedia. Siemens. Återställd från: es.wikipedia.org.


Ingen har kommenterat den här artikeln än.