
Vad är periodens funktion y = 3sen (4x)?
De funktionsperiod y = 3sen (4x) är 2π / 4 = π / 2. För att klart förstå orsaken till detta uttalande måste definitionen av periodens funktion och periodens funktion sin (x) vara känd; lite om diagram av funktioner kommer också att vara användbart.
Trigonometriska funktioner, såsom sinus och cosinus (sin (x) och cos (x)), är mycket användbara i både matematik och teknik.
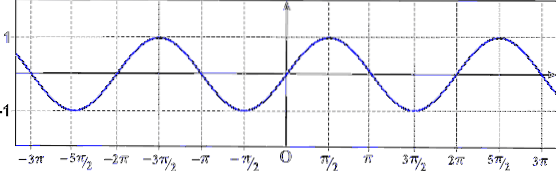
Ordet period hänvisar till repetitionen av en händelse, så att säga att en funktion är periodisk motsvarar att säga "dess graf är repetitionen av en kurvbit." Som kan ses i föregående bild är funktionen sin (x) periodisk.
Periodiska funktioner
En funktion f (x) sägs vara periodisk om det finns ett verkligt värde p ≠ 0 så att f (x + p) = f (x) för alla x i domänen för funktionen. I detta fall är funktionsperioden p.
Funktionens period kallas vanligtvis det minsta positiva realtalet p som uppfyller definitionen.
Som kan ses i föregående graf är funktionen sin (x) periodisk och dess period är 2π (cosinusfunktionen är också periodisk, med en period lika med 2π).
Ändringar i grafen för en funktion
Låt f (x) vara en funktion vars graf är känd, och låt c vara en positiv konstant. Vad händer med grafen för f (x) om f (x) multipliceras med c? Med andra ord, vad är grafen för c * f (x) och f (cx)?
Diagram över c * f (x)
Vid multiplicering av en funktion, externt, med en positiv konstant, genomgår grafen för f (x) en förändring av utgångsvärdena; förändringen är vertikal och det finns två fall:
- Om c> 1, genomgår diagrammet en vertikal sträcka med faktorn c.
- Ja 0 När argumentet för en funktion multipliceras med en konstant, genomgår grafen för f (x) en förändring av ingångsvärdena; förändringen är horisontell och som tidigare kan det finnas två fall: - Om c> 1 genomgår diagrammet horisontell kompression med faktorn 1 / c. - Ja 0 Det bör noteras att i funktionen f (x) = 3sen (4x) finns det två konstanter som ändrar grafen för sinusfunktionen: en multipliceras externt och den andra internt.. 3 som ligger utanför sinusfunktionen vad den gör är att förlänga funktionen vertikalt med en faktor 3. Detta innebär att grafen för funktion 3 sin (x) kommer att ligga mellan värdena 3 och 3. 4 inuti sinusfunktionen gör att grafen för funktionen genomgår horisontell kompression med en faktor på 1/4. Å andra sidan mäts en funktionsperiod horisontellt. Eftersom funktionsperioden sin (x) är 2π, med tanke på sin (4x) kommer periodens storlek att förändras. För att ta reda på vilken period y = 3sen (4x) är, multiplicerar du bara perioden för funktionen sin (x) med 1/4 (kompressionsfaktorn). Med andra ord är periodens funktion y = 3sin (4x) 2π / 4 = π / 2, vilket kan ses i den sista grafen.Diagram över f (cx)
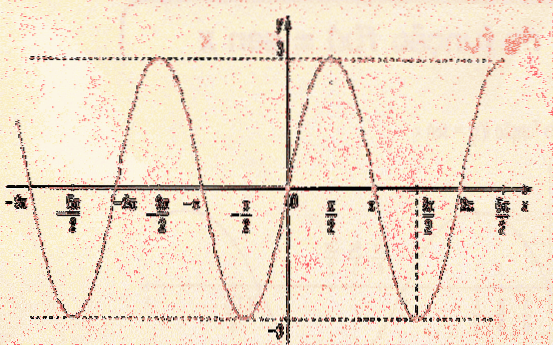
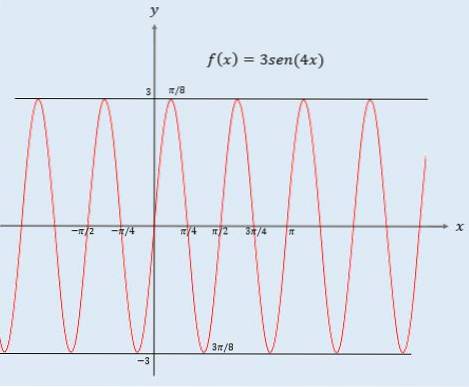
Funktionsperiod y = 3sen (4x)
Referenser



Ingen har kommenterat den här artikeln än.