
Vad är skillnaden mellan väg och förskjutning?
De huvudskillnaden mellan bana och förskjutning är att det senare är avståndet och riktningen som ett objekt har rest, medan det förra är den väg eller form som objektets rörelse tar.
För att tydligare se skillnaderna mellan förskjutning och bana är det bättre att specificera dess konceptualisering genom exempel som möjliggör en bättre förståelse av båda termerna..
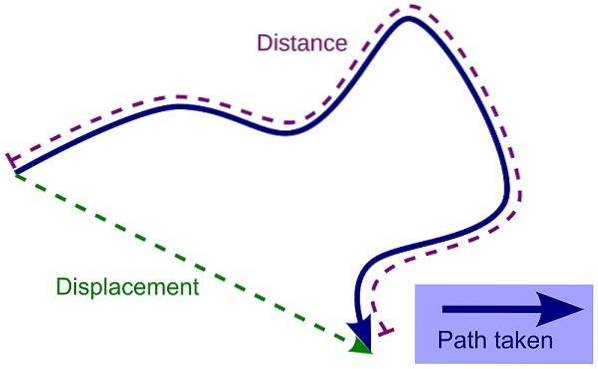
Förflyttning
Det förstås som avståndet och riktningen som ett objekt har rest med hänsyn till dess ursprungliga position och dess slutliga position, alltid i rak linje. För dess beräkning, eftersom det är en vektorstorlek, används måtten på längden som kallas centimeter, meter eller kilometer..
Formeln för att beräkna förskjutningen definieras enligt följande:
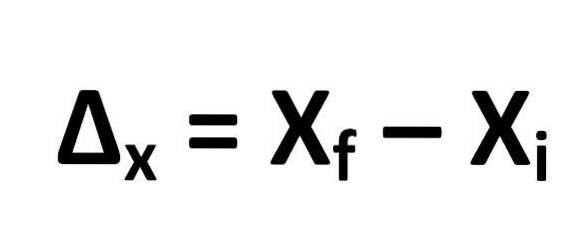
Därav följer att:
- Δx = förskjutning
- XF = slutlig position för objektet
- Xi = objektets ursprungliga position
Förskjutningsexempel
1- Om en grupp barn befinner sig i början av en rutt, vars utgångsläge är 50 m, rör sig i en rak linje, bestäm förskjutningen vid var och en av punkterna XF .
- XF = 120m
- XF = 90m
- XF = 60m
- XF = 40m
2- Problemets data extraheras genom att ersätta X-värdenatvå och X1 i offsetformeln:
- Δx = ?
- Xi = 50m
- Δx = XF - Xi
- Δx = 120m - 50m = 70m
3- I detta första tillvägagångssätt säger vi att Δx är lika med 120m, vilket motsvarar det första värdet vi hittar på XF, minus 50 m vilket är värdet på Xi, Resultatet är 70m, det vill säga när förflyttningen når 120m var förskjutningen 70m till höger.
4- Vi fortsätter att lösa på samma sätt för värdena b, c och d
- Δx = 90m - 50m = 40m
- Δx = 60m - 50m = 10m
- Δx = 40m - 50m = - 10m
I detta fall gav förskjutningen oss negativa, det betyder att slutpositionen är i motsatt riktning till utgångsläget.
Bana
Det är den rutt eller linje som bestäms av ett objekt under dess rörelse och dess utvärdering i det internationella systemet, antar i allmänhet geometriska former som linjen, parabolen, cirkeln eller ellipsen). Den identifieras genom en imaginär linje och eftersom den är en skalär kvantitet mäts den i meter.
Det bör noteras att för att beräkna banan måste vi veta om kroppen är i vila eller rörelse, det vill säga den utsätts för det referenssystem som vi väljer.
Ekvationen för att beräkna ett objekts bana i det internationella systemet ges av:
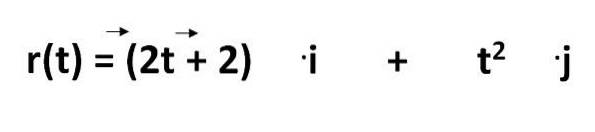
Varav vi måste:
- r (t) = är banans ekvation
- 2t - 2 och ttvå = representerar koordinater som en funktion av tiden
- .jag och .j = är enhetsvektorerna
För att förstå beräkningen av den väg som ett objekt har rest, kommer vi att utveckla följande exempel:
- Beräkna ekvationen för banorna för följande positionsvektorer:
- r (t) = (2t + 7) .i + ttvå .j
- r (t) = (t - 2) .i + 2t .j
Första steget: Eftersom en vägekvation är en funktion av X, definierar du värdena för X respektive Y i var och en av de föreslagna vektorerna:
1- Lös första positionsvektorn:
- r (t) = (2t + 7) .i + ttvå .j
2- Ty = f (x), där X ges av innehållet i enhetsvektorn .i och Y ges av innehållet i enhetsvektorn .j:
- X = 2t + 7
- Y = ttvå
3- y = f (x), det vill säga tiden är inte en del av uttrycket, därför måste vi lösa det, vi har:
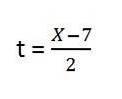
4 - Vi ersätter rensningen i Y. Det återstår:
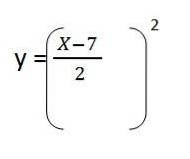
5- Vi löser innehållet inom parenteser och vi har ekvationen för den resulterande vägen för den första enhetsvektorn:
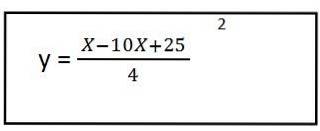
Som vi kan se gav det oss en andra grads ekvation, detta betyder att banan har formen av en parabel.
Andra steg: Vi fortsätter på samma sätt för att beräkna banan för den andra enhetsvektorn
r (t) = (t - 2) .i + 2t .j
- X = t - 2
- Y = 2t
2- Efter stegen som vi såg tidigare y = f (x), måste vi rensa tiden eftersom det inte är en del av uttrycket, vi sitter kvar med:
- t = X + 2
3- Vi ersätter klarering i Y, återstående:
- y = 2 (X + 2)
4- För att lösa parenteser har vi ekvationen för den resulterande banan för den andra enhetsvektorn:
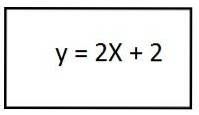
I det här förfarandet blev resultatet en rak linje, som berättar att banan har en rätlinjig form.
När begreppen förskjutning och bana har förståts kan vi härleda resten av skillnaderna som finns mellan båda termerna.
Fler skillnader mellan förskjutning och bana
Förflyttning
- Det är avståndet och riktningen som ett objekt har rest med hänsyn till dess ursprungliga position och dess slutliga position.
- Det händer alltid i rak linje.
- Det känns igen med en pil.
- Använd längdmätningar (centimeter, meter, kilometer).
- Det är en vektorkvantitet.
- Ta hänsyn till körriktningen (till höger eller vänster)
- Det tar inte hänsyn till den tid som spenderas under turnén.
- Beror inte på ett referenssystem.
- När startpunkten är samma startpunkt är förskjutningen noll.
- Modulen måste sammanfalla med färdutrymmet så länge vägen är en rak linje och det finns inga förändringar i riktningen att följa.
- Modulen tenderar att öka eller minska när rörelsen sker, med tanke på banan.
Bana
Det är den väg eller linje som bestäms av ett objekt under dess rörelse. Antar geometriska former (raka, paraboliska, cirkulära eller elliptiska).
- Det representeras av en imaginär linje.
- Det mäts i meter.
- Det är en skalär kvantitet.
- Den tar inte hänsyn till den körda riktningen.
- Tänk på tiden som spenderades under turnén.
- Beror på ett referenssystem.
- När startpunkten eller utgångsläget är samma som slutpositionen ges banan av det sträcka som har rest.
- Värdet på banan sammanfaller med förskjutningsvektorens modul, om den resulterande banan är en rak linje, men det finns inga förändringar i riktningen att följa.
- Ökar alltid när kroppen rör sig, oavsett banan.
Referenser
- Alvarado, N. (1972) Fysiskt. Första året av vetenskap. Ledare Fotoprin C.A. Venezuela.
- Fernández, M; Fidalgo, J. (2016). Fysik och kemi 1: a Baccalaureat. Editions Paraninfo, S.A. Spanien.
- Guatemalas institut för radioutbildning. (2011) Grundläggande fysik. Zaculeu Group första terminen. Guatemala.
- Fernández, P. (2014) Vetenskapligt-teknologiskt område. Paraninfo-utgåvor. S.A. Spanien.
- Fisica Lab (2015) Vector Displacement. Återställd från: fisicalab.com.
- Exempel på. (2013) förskjutning. Återställd från: examplesde.com.
- Vardagsrumsprojekt (2014) Vad är förskjutning? Återställd från: salonhogar.net.
- Physics Lab (2015) Begreppet bana och positionsekvation. Återställd från: fisicalab.com.



Ingen har kommenterat den här artikeln än.