
Gratis kroppsdiagram hur man gör det, exempel, träning
A Fri kroppsdiagram, isolerat kroppsdiagram eller kraftdiagram, är ett diagram där krafterna som verkar på en kropp representeras av pilar.
Se till att inkludera i diagrammet Allt de krafter som verkar på objektet, och eftersom det är en vektormängd, är pilen ansvarig för att indikera dess riktning och dess avkänning, medan dess längd ger en uppfattning om modul eller intensitet.
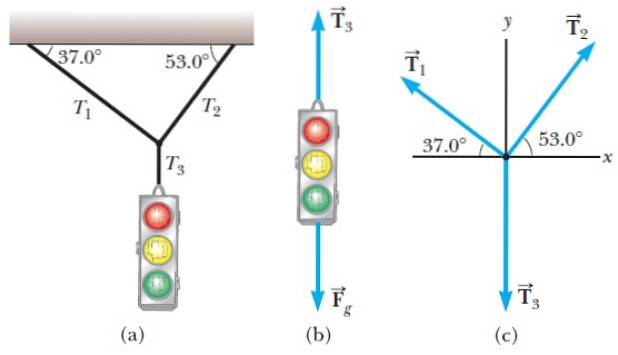
I figur 1 har vi ett exempel på ett frikroppsdiagram som vi ska analysera.
Situationen är som följer: ett trafikljus som hänger i vila från vissa kablar (figur 1a). Två krafter verkar på den, en är den som utövas av jorden, vilket är vikt. I diagrammet betecknas det som Fg och agerar vertikalt nedåt.
Den andra kraften är spänningen i den vertikala strängen, kallad T3 och det går i vertikal riktning uppåt, håller trafikljuset och förhindrar att det faller till marken.
När ett problem har mer än ett objekt är det nödvändigt att rita ett diagram för var och en separat..
Knuten mellan lutande rep och repet som håller trafikljuset anses vara ett punktobjekt och dess fria kroppsdiagram är i figur 1c. Observera att för knuten, spänningen T3 riktas nedåt.
Det är viktigt att notera att de krafter som objektet utövar på andra kroppar inte ska visas i frikroppsdiagrammet utan bara de som agerar på det.
Artikelindex
- 1 Exempel på frikroppsdiagram
- 1.1 En person som drar en bagageutrymme eller container
- 1.2 Ett block som glider nedåt i ett lutande plan
- 1.3 Atwoods maskin
- 2 Övningen löst
- 2.1 Lösning
- 3 Referenser
Exempel på frikroppsdiagram
Det fria kroppsdiagrammet gör det möjligt att tillämpa Newtons lagar och med dem bestämma tillståndet för rörelse eller vila på det föremål som krafterna verkar på. När det gäller trafikljuset som visas kan vi bestämma värdet på spänningarna i kablarna som håller trafikljuset, med vetskap om vikten av detta.
När dessa data är kända väljs lämpliga kablar för att hänga trafikljuset och som uppfyller deras funktion utan att kollapsa.
Frikroppsdiagram används för att beskriva olika vardagliga situationer, såsom dessa:
En person som drar en bagageutrymme eller container
Det är mycket vanligt att människor måste bära tunga föremål som containern i figuren. För att göra detta måste de utöva en kraft F om behållaren, som i detta exempel är horisontellt och till höger, vilket är rörelseriktningen.
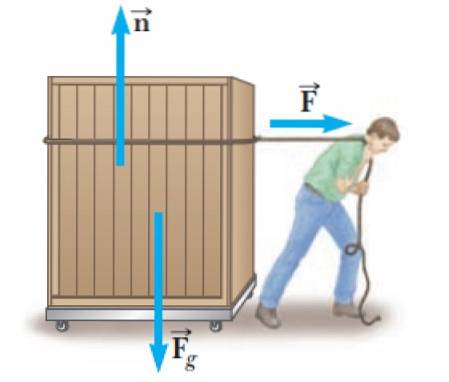
Men det här är inte den enda kraften som verkar på honom, det finns också det normala n, utövas av hjulplattformens plana yta. Och slutligen finns det vikten av det: Fg, riktas vertikalt nedåt.
Det normala är en kraft som uppstår när två ytor är i kontakt och alltid är vinkelrät mot ytan som utövar den. I detta fall utövar hjulplattformen en normal på containern.
Ett block som glider neråt i ett lutande plan
Vissa skrivbord har bordet lutat något för att göra det lättare att anteckna och läsa. Det har också en pennhållare, men vi har alla lagt pennan på bordet ur spåret och vi har sett hur den glider på bordet.
Vilka krafter verkar på pennan?
Samma som fungerar på blocket som visas i följande frikroppsdiagram:
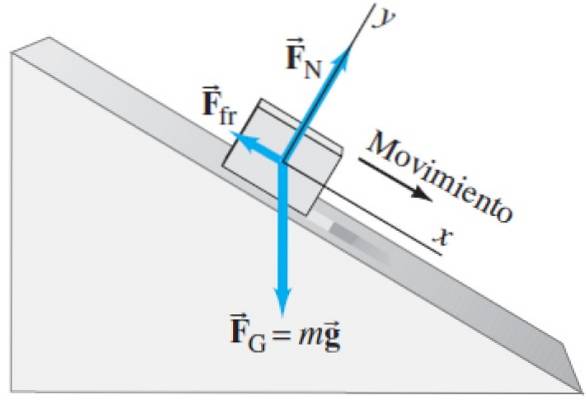
Det normala FN är den kraft som bordsytan utövar på den stödda pennan eller blocket. Till skillnad från föregående exempel är det normala inte vertikalt, utan snett. Kom ihåg att det normala är den kraft som tabellen utövar på blocket och är vinkelrät mot det. Eftersom bordet lutas, är det vanliga också.
Som alltid vikten Fg är vertikalt, oavsett systemets lutning.
Och slutligen har vi en ny kraftverkande, vilket är kinetisk friktion Ffr mellan bordet och pennan eller blocket. Friktion är också en kontaktkraft, men till skillnad från normalt är den en tangentiell (parallell) kraft mot ytan. Observera också att den alltid riktas i motsatt riktning mot rörelse..
Atwoods maskin
Atwood-maskinen är en enkel maskin som består av en lätt, friktionsfri remskiva på skenan, genom vilken ett lätt och osträckbart rep passerar.
Två objekt med massa m hängs från den1 och Mtvå. När ett av objekten går upp, går det andra ned, som visas i figur 4a:
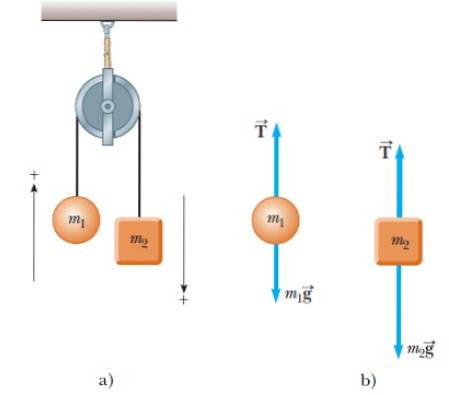
Eftersom det finns två objekt skapas ett frikroppsdiagram för var och en separat. För båda föremålen finns det bara två krafter: spänningen i strängen T och respektive vikter.
I figuren uttrycks varje vikt direkt som mass- och accelerationsprodukten. För sin del riktas spänningen alltid vertikalt längs det spända repet.
Övningen löst
Tillämpa Newtons lagar för att bestämma accelerationen med vilken massorna rör sig från Atwood-maskinen som visas i föregående avsnitt.
Lösning
Newtons andra lag säger att summan av krafterna är lika med massprodukten och accelerationen.
Tecknet konventionen i varje massa kan vara annorlunda, så vi kommer att ta rörelse som en positiv känsla, som anges i diagrammet, den första massan stiger och den andra faller.
I vissa problem ger uttalandet inte information, då måste tecknen tilldelas godtyckligt och om resultatet av accelerationen är negativt, rör sig masssystemet i motsatt riktning till det ursprungligen antagna.
-För massa 1 (stiger):
T - m1g = m1till
-För massa 2 (låg):
-T + mtvåg = mtvåtill
Båda ekvationerna bildar ett system med linjära ekvationer av två okända, eftersom spänningen uppträder med olika tecken i varje ekvation, vi lägger dem helt enkelt ord för ord och spänningen avbryts:
mtvåg - m1g = m1a + mtvåtill
a = mtvåg - m1g / (m1 + mtvå)
Referenser
- Bauer, W. 2011. Fysik för teknik och vetenskap. Volym 1. Mc Graw Hill.
- Giancoli, D. 2006. Fysik: principer med tillämpningar. 6: e. Ed prentice hall.
- Serway, R., Vulle, C. 2011. College Physics. 9: e upplagan Cengage Learning.
- Tipler, P. (2006) Fysik för vetenskap och teknik. 5: e upplagan Volym 1. Redaktionellt Reverté.
- Tippens, P. 2011. Fysik: begrepp och tillämpningar. 7: e upplagan. Mcgraw hill


Ingen har kommenterat den här artikeln än.