Skillnad mellan kuberformler, ekvationer, exempel, övningar

De skillnad på kuber är ett binomialt algebraiskt uttryck av formen a³ - b³, där termerna a och b kan vara reella tal eller algebraiska uttryck av olika slag. Ett exempel på en skillnad på kuber är: 8 - x³, eftersom 8 kan skrivas som 2³.

Geometriskt kan vi tänka oss en stor kub, med sida a, från vilken den lilla kuben med sida b subtraheras, såsom illustreras i figur 1:

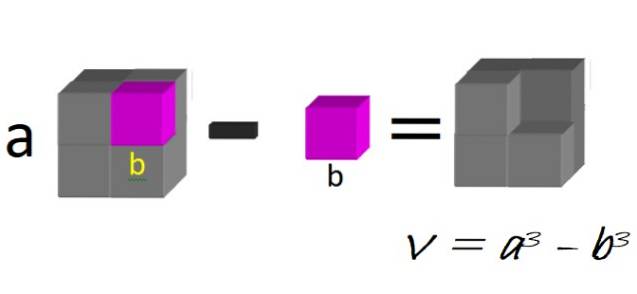
Volymen på den resulterande figuren är exakt en skillnad i kuber:

V = a³ - b³

För att hitta ett alternativt uttryck observeras att denna siffra kan sönderdelas i tre prismer, som visas nedan:

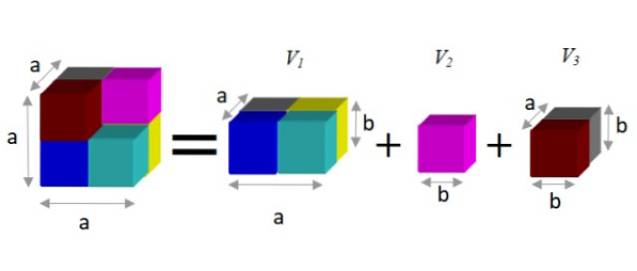
Ett prisma har en volym som ges av produkten med sina tre dimensioner: bredd x höjd x djup. På detta sätt är den resulterande volymen:

V = a³ - b³ = a^två.b + b³ + a.b^två

Faktorn b det är vanligt till höger. Dessutom är det i figuren som visas ovan särskilt sant att:

b = (a / 2) ⇒ a = b + b

Därför kan man säga att: b = a - b. Således:

till³ - b³ = b (a^två + b^två +a.b) = (a-b) (a^två + a.b + b^två)

Detta sätt att uttrycka skillnaden i kuber kommer att visa sig vara mycket användbart i många applikationer och skulle ha uppnåtts på samma sätt, även om den saknade kubens sida i hörnet var annorlunda än b = a / 2.

Observera att den andra parentesenser mycket ut som den anmärkningsvärda produkten av summan av summan, men tvärtermen multipliceras inte med 2. Läsaren kan utveckla rätt sida för att verifiera att den faktiskt erhålls till³ - b³.

Artikelindex

• 1 Exempel
  • 1.1 Fakturering av en kubskillnad
• 2 Övningen löst
  • 2.1 Övning 1
  • 2.2 Övning 2
• 3 Referenser

Exempel

Det finns flera skillnader i kuber:

1 - m⁶

till⁶b³ - 8z¹²Y⁶

(1/125) .x⁶ - 27 och⁹

Låt oss analysera var och en av dem. I det första exemplet kan 1 skrivas som 1 = 1³ och termen m⁶ kvarstår: (m^två)³. Båda termerna är perfekta kuber, därför är deras skillnad:

1 - m⁶ = 1³ - (m^två)³

I det andra exemplet skrivs termerna om:

till⁶b³ = (a^tvåb)³

8z¹²Y⁶ = 2³ (z⁴)³ (Y^två)³ = (2z⁴Y^två)³

Skillnaden mellan dessa kuber är: (a^tvåb)³ - (2z⁴Y^två)³.

Slutligen är fraktionen (1/125) (1/5³), x⁶ = (x^två)³, 27 = 3³ och och⁹ = (och³)³. Genom att ersätta allt detta i det ursprungliga uttrycket får du:

(1/125) .x⁶  - 27 år⁹ = [(1/5) (x^två)]³ - (3 år³)³

Faktorerar en skillnad på kuber

Att faktorisera skillnaden mellan kuber förenklar många algebraiska operationer. För att göra detta räcker det att använda formeln ovan:

Nu består proceduren för att tillämpa denna formel i tre steg:

- Först erhålls kubroten för var och en av skillnaderna.

- Sedan konstrueras binomialet och trinomialet som visas på höger sida av formeln.

- Slutligen ersätts binomialet och trinomialet för att erhålla den slutgiltiga faktoriseringen.

Låt oss illustrera användningen av dessa steg med vart och ett av kubskillnadsexemplen som föreslagits ovan och därmed erhålla dess beräknade motsvarighet.

Exempel 1

Faktorera uttrycket 1 - m⁶   följer stegen som beskrivs. Vi börjar med att skriva om uttrycket som 1 - m⁶ = 1³ - (m^två)³ för att extrahera respektive kubrötter för varje term:

Därefter konstrueras binomialet och trinomialet:

a = 1

b = m^två

Sedan:

a - b = 1 - m^två

 (till^två +a.b + b^två) = 1^två + 1.m^två + (m^två)^två = 1 + m^två + m⁴

 Slutligen ersätts den med formeln a³ - b³ = (a-b) (a^två +a.b + b^två):

1 - m⁶ = (1 - m^två) (1 + m^två + m⁴)

Exempel 2

Faktorisera:

till⁶b³ -8z¹²Y⁶ = (a^tvåb)³ - (2z⁴Y^två)³

Eftersom det här är perfekta kuber är kubrötterna omedelbara: a^tvåb och 2z⁴Y^två, därav följer att:

- Binomial: a^tvåb - 2z⁴Y^två

- Trinomial: (a^tvåb)^två + till^tvåb. 2z⁴Y^två + (till^tvåb + 2z⁴Y^två)^två

 Och nu är den önskade faktoriseringen konstruerad:

till⁶b³ -8z¹²Y⁶ = (a^tvåb - 2z⁴Y^två). [(till^tvåb)^två + till^tvåb. 2z⁴Y^två + (till^tvåb + 2z⁴Y^två)^två] =

= (a^tvåb - 2z⁴Y^två). [till⁴b^två + 2: a^tvåb.z⁴Y^två + (till^tvåb + 2z⁴Y^två)^två]

I princip är factoring klar, men det är ofta nödvändigt att förenkla varje termin. Sedan utvecklar vi den anmärkningsvärda produkten - kvadrat av en summa - som dyker upp i slutet och lägger sedan till liknande termer. Kom ihåg att kvadraten på en summa är:

(x + y)^två = x^två + 2xy + och^två

Den anmärkningsvärda produkten till höger är utvecklad så här:

(till^tvåb + 2z⁴Y^två)^två = a⁴b^två + 4: e^tvåb.z⁴Y^två + 4z⁸Y⁴

 Ersätter den erhållna expansionen i faktorisering av skillnaden i kuber:

till⁶b³ -8z¹²Y⁶ = (a^tvåb - 2z⁴Y^två). [till⁴b^två + 2: a^tvåb.z⁴Y^två + till⁴b^två + 4: e^tvåb.z⁴Y^två + 4z⁸Y⁴] =

Slutligen, gruppera liknande termer och ta med de numeriska koefficienterna, som alla är jämna, får vi:

(till^tvåb - 2z⁴Y^två). [2a⁴b^två + 6: e^tvåb.z⁴Y^två + 4z⁸Y⁴] = 2 (a^tvåb - 2z⁴Y^två). [till⁴b^två + 3: e^tvåb.z⁴Y^två + 2z⁸Y⁴]

Exempel 3

Faktor (1/125) .x⁶  - 27 år⁹ det är mycket enklare än det tidigare fallet. Först identifieras ekvivalenterna a och b:

a = (1/5) x^två

b = 3y³

Sedan ersätts de direkt i formeln:

(1/125) .x⁶  - 27 år⁹ = [(1/5) x^två - 3y³]. [(1/25) x⁴ + (3/5) x^tvåY³ + 9y⁶]

Övningen löst

Skillnaden mellan kuber har, som vi har sagt, en mängd olika applikationer i Algebra. Låt oss se några:

Övning 1

Lös följande ekvationer:

yxa⁵ - 125 x^två = 0

b) 64 - 729 x³ = 0

Lösning till

Först faktureras ekvationen på detta sätt:

x^två (x³ - 125) = 0

Eftersom 125 är en perfekt kub, skrivs parenteserna som en skillnad på kuber:

x^två . (x³ - 5³) = 0

Den första lösningen är x = 0, men vi hittar mer om vi gör x³ - 5³ = 0, sedan:

x³ = 5³ → x = 5

Lösning b

Vänster sida av ekvationen skrivs om till 64 - 729 x³ = 4³ - (9x)³. Därför:

4³ - (9x)³ = 0

Eftersom exponenten är densamma:

9x = 4 → x = 9/4

Övning 2

Faktorera uttrycket:

(x + y)³ - (x - y)³

Lösning

Detta uttryck är en skillnad på kuber, om vi i factoringformeln noterar att:

a = x + y

b = x- y

Sedan konstrueras binomialet först:

a - b = x + y - (x- y) = 2y

Och nu steget:

till^två + a.b + b^två = (x + y)^två + (x + y) (x-y) + (x-y)^två

Anmärkningsvärda produkter utvecklas:

(x + y)^två = x^två + 2xy + och^två

(x + y) (x-y) = x^två- Y^två

(x- y)^två = x^två - 2xy + och^två

Därefter måste du ersätta och minska liknande termer:

till^två + a.b + b^två = x^två + 2xy + och^två+ x^två- Y^två+ x^två - 2xy + och^två = 3x^två + Y^två

Faktoring resulterar i:

(x + y)³ - (x - y)³ = 2 år. (3x^två + Y^två)

Referenser

1. Baldor, A. 1974. Algebra. Redaktionellt Cultural Venezolana S.A.
2. CK-12 Foundation. Summa och skillnad på kuber. Återställd från: ck12.org.
3. Khan akademin. Fakturering av skillnader i kuber. Återställd från: es.khanacademy.org.
4. Math is Fun Advanced. Skillnad mellan två kuber. Återställd från: mathsisfun.com
5. UNAM. Faktorerar en skillnad på kuber. Återställd från: dcb.fi-c.unam.mx.