
Diskreta sannolikhetsfördelningsegenskaper, övningar
De diskreta sannolikhetsfördelningar de är en funktion som tilldelar varje element av X (S) = x1, x2, ..., xi, ..., där X är en given diskret slumpmässig variabel och S är dess samplingsutrymme, sannolikheten för att nämnda händelse inträffar. Denna funktion f av X (S) definierad som f (xi) = P (X = xi) kallas ibland sannolikhetsmassfunktionen.
Denna sannolikhetsmassa visas generellt i tabellform. Eftersom X är en diskret slumpmässig variabel har X (S) ett ändligt antal händelser eller räknas oändlighet. Bland de vanligaste diskreta sannolikhetsfördelningarna har vi den enhetliga fördelningen, binomialfördelningen och Poissonfördelningen.
Artikelindex
- 1 Funktioner
- 2 typer
- 2.1 Enhetlig fördelning över n poäng
- 2.2 Binomial fördelning
- 2.3 Poissonfördelning
- 2.4 Hypergeometrisk fördelning
- 3 Lösta övningar
- 3.1 Första övningen
- 3.2 Andra övningen
- 3.3 Tredje övningen
- 3.4 Tredje övningen
- 4 Referenser
Egenskaper
Sannolikhetsfördelningsfunktionen måste uppfylla följande villkor:
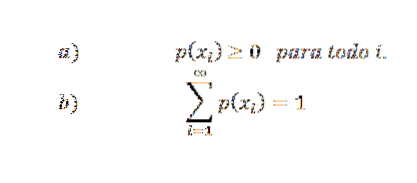
Dessutom, om X bara tar ett ändligt antal värden (till exempel x1, x2, ..., xn), då blir p (xi) = 0 om i> ny, därför blir den oändliga serien av tillstånd b en slutlig serie.
Denna funktion uppfyller också följande egenskaper:
Låt B vara en händelse associerad med den slumpmässiga variabeln X. Detta betyder att B ingår i X (S). Antag specifikt att B = xi1, xi2,…. Därför:
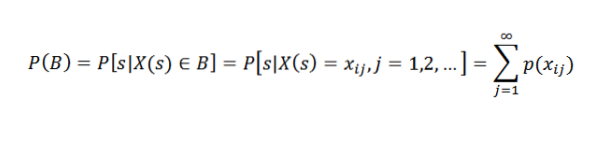
Med andra ord: sannolikheten för en händelse B är lika med summan av sannolikheterna för de enskilda resultaten som är associerade med B.
Av detta kan vi dra slutsatsen att om a < b, los sucesos (X ≤ a) y (a < X ≤ b) son mutuamente excluyentes y, además, su unión es el suceso (X ≤ b), por lo que tenemos:
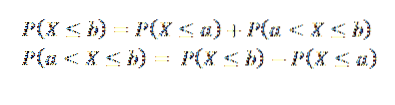
Typer
Enhetlig fördelning över n punkter
En slumpmässig variabel X sägs följa en fördelning som kännetecknas av att vara enhetlig vid n-punkter om varje värde tilldelas samma sannolikhet. Dess sannolikhetsmassfunktion är:
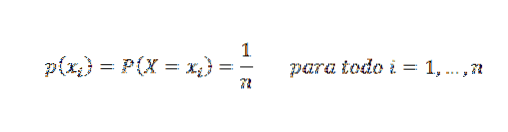
Anta att vi har ett experiment som har två möjliga resultat, det kan vara kastet av ett mynt vars möjliga resultat är huvuden eller svansar, eller valet av ett heltal vars resultat kan vara ett jämnt eller udda; denna typ av experiment kallas Bernoulli-tester.
I allmänhet kallas de två möjliga resultaten framgång och misslyckande, där p är sannolikheten för framgång och 1-p är sannolikheten för misslyckande. Vi kan bestämma sannolikheten för x-framgångar i n Bernoulli-tester som är oberoende av varandra med följande fördelning.
Binomial distribution
Det är funktionen som representerar sannolikheten för att uppnå x-framgångar i n oberoende Bernoulli-test, vars sannolikhet för framgång är p. Dess sannolikhetsmassfunktion är:
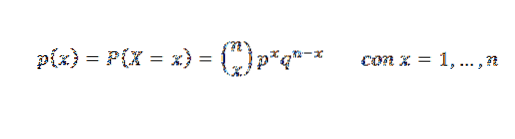
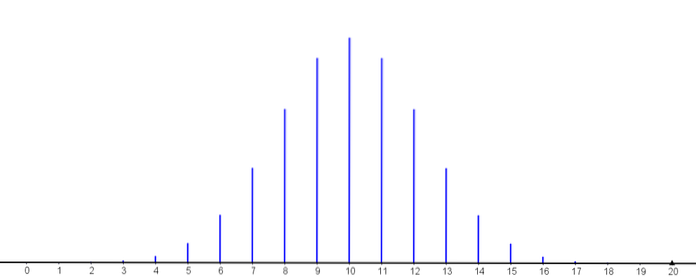
Följande graf representerar sannolikhetsmassfunktionen för olika värden för parametrarna för binomialfördelningen.
Följande distribution har sitt namn till den franska matematikern Simeon Poisson (1781-1840), som fick det som gränsen för binomialfördelningen.
Poisson distribution
En slumpmässig variabel X sägs ha en Poisson-fördelning av parametern λ när den kan ta de positiva heltalsvärdena 0,1,2,3, ... med följande sannolikhet:
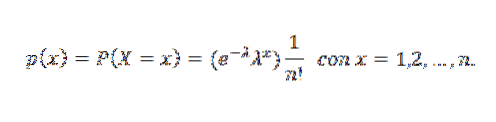
I detta uttryck är λ det genomsnittliga antalet som motsvarar förekomsten av händelsen för varje tidsenhet, och x är antalet gånger händelsen inträffar.
Dess sannolikhetsmassfunktion är:
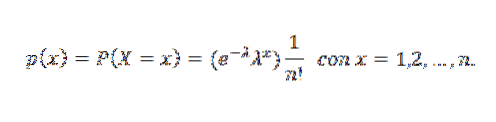
Därefter ett diagram som representerar sannolikhetsfunktionen för olika värden för parametrarna för Poisson-fördelningen.
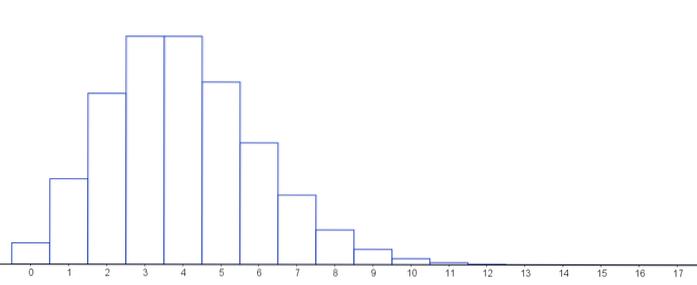
Observera att så länge antalet framgångar är lågt och antalet tester som utförs på en binomialfördelning är hög, kan vi alltid approximera dessa fördelningar, eftersom Poisson-fördelningen är gränsen för binomialfördelningen.
Huvudskillnaden mellan dessa två fördelningar är att medan binomialet beror på två parametrar - nämligen n och p-, beror Poisson bara på λ, som ibland kallas distributionsintensiteten..
Hittills har vi bara pratat om sannolikhetsfördelningar för fall där de olika experimenten är oberoende av varandra. det vill säga när resultatet av en inte påverkas av något annat resultat.
När det förekommer experiment som inte är oberoende är den hypergeometriska fördelningen mycket användbar.
Hypergeometrisk fördelning
Låt N vara det totala antalet objekt i en ändlig uppsättning, av vilka vi på något sätt kan identifiera k av dessa och därmed bilda en delmängd K, vars komplement bildas av de återstående N-k-elementen.
Om vi slumpmässigt väljer n objekt har den slumpmässiga variabeln X som representerar antalet objekt som tillhör K i nämnda val en hypergeometrisk fördelning av parametrarna N, n och k. Dess sannolikhetsmassfunktion är:
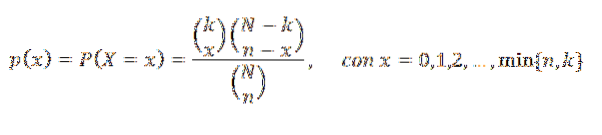
Följande graf representerar sannolikhetsmassafunktionen för olika värden för parametrarna för den hypergeometriska fördelningen.
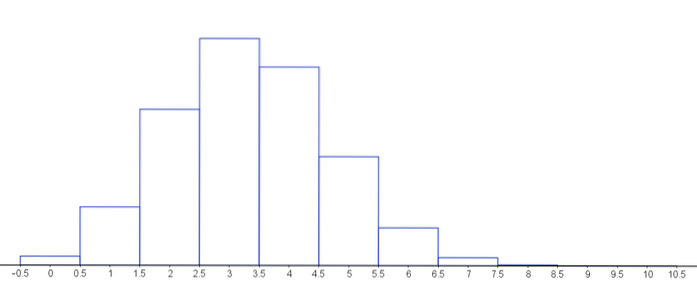
Lösta övningar
Första övningen
Antag att sannolikheten för att ett radiorör (placerat i en viss typ av utrustning) kommer att fungera i mer än 500 timmar är 0,2. Om 20 rör testas, vad är sannolikheten att exakt k av dessa kommer att gå i mer än 500 timmar, k = 0, 1,2,…, 20?
Lösning
Om X är antalet rör som fungerar mer än 500 timmar, antar vi att X har en binomial fördelning. Sedan
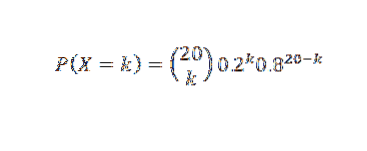
Och så:

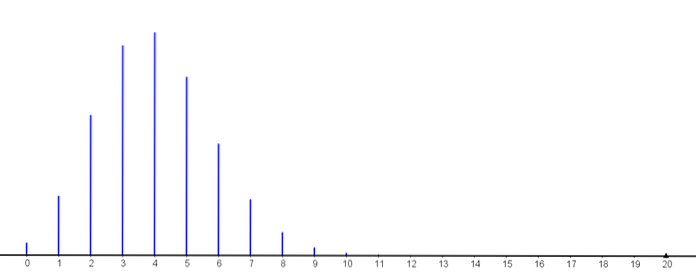
För k≥11 är sannolikheterna mindre än 0,001
Således kan vi observera hur sannolikheten att k av dessa fungerar i mer än 500 timmar ökar tills den når sitt maximala värde (med k = 4) och sedan börjar minska..
Andra övningen
Ett mynt kastas 6 gånger. När resultatet är dyrt kommer vi att säga att det är en framgång. Vad är sannolikheten för att två huvuden kommer upp exakt?
Lösning
För detta fall har vi n = 6 och både sannolikheten för framgång och misslyckande är p = q = 1/2
Därför är sannolikheten att två huvuden ges (det vill säga k = 2)
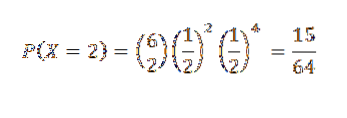
Tredje övningen
Vad är sannolikheten för att hitta minst fyra huvuden?
Lösning
För detta fall har vi att k = 4, 5 eller 6
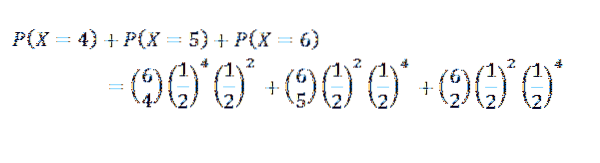
Tredje övningen
Antag att 2% av artiklarna som produceras i en fabrik är defekta. Hitta sannolikheten P att det finns tre defekta objekt i ett urval på 100 artiklar.
Lösning
I det här fallet kan vi använda binomialfördelningen för n = 100 och p = 0,02, vilket får som resultat:
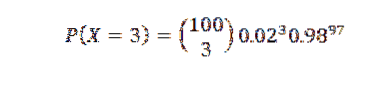
Eftersom p är liten använder vi dock Poisson-approximationen med λ = np = 2. A) Ja,
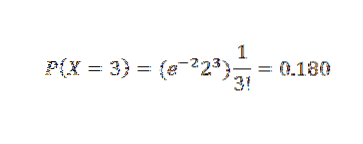
Referenser
- Kai Lai Chung. Elementär möjlighetsteori med stokastiska processer. Springer-Verlag New York Inc.
- Kenneth H. Rosen. Diskret matematik och dess tillämpningar. S.A. MCGRAW-HILL / INTERAMERICANA DE ESPAÑA.
- Paul L. Meyer. Sannolikhet och statistiska tillämpningar. S.A. MEXIKANSKA ALHAMBRA.
- Seymour Lipschutz Ph.D. 2000 Lösta problem med diskret matematik. McGRAW-HILL.
- Seymour Lipschutz Ph.D. Teori och sannolikhetsproblem. McGRAW-HILL.



Ingen har kommenterat den här artikeln än.