Allmän ekvation för en linje vars lutning är lika med 2/3

Den allmänna ekvationen för en linje L är följande: Ax + By + C = 0, där A, B och C är konstanter, x är den oberoende variabeln och och den beroende variabeln.

Lutningen på en linje, generellt betecknad med bokstaven m, som passerar genom punkterna P = (x1, y1) och Q = (x0, y0) är följande kvot m: = (y1-y0) / (x1 -x0 ).

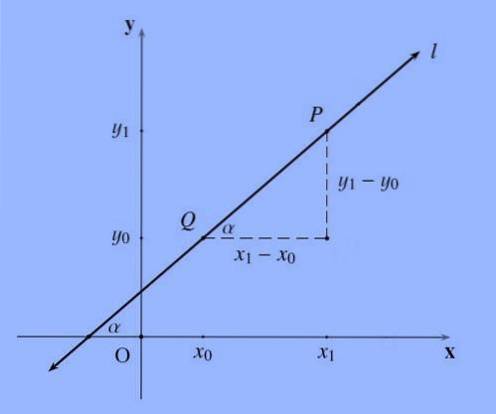
Lutningen på en linje representerar på ett visst sätt lutningen; Mer formellt är linjens lutning tangenten för den vinkel den bildar med X-axeln..

Det bör noteras att ordningen i vilken punkterna är namngivna är likgiltig, eftersom (y0-y1) / (x0-x1) = - (y1-y0) / (- (x1-x0)) = (y1-y0) / (x1-x0).

Lutning av en linje

Om man känner till två punkter genom vilka en linje passerar är det lätt att beräkna dess lutning. Men tänk om dessa punkter inte är kända?

Med tanke på den allmänna ekvationen för en linje Ax + By + C = 0 är dess lutning m = -A / B.

Vad är den allmänna ekvationen för en linje vars lutning är 2/3?

Eftersom linjens lutning är 2/3 fastställs jämställdheten -A / B = 2/3, med vilken vi kan se att A = -2 och B = 3. Så den allmänna ekvationen för en linje med lutning lika med 2/3 är -2x + 3y + C = 0.

Det bör klargöras att om A = 2 och B = -3 väljs kommer samma ekvation att erhållas. I själva verket är 2x-3y + C = 0, vilket är lika med det föregående multiplicerat med -1. Tecknet på C spelar ingen roll eftersom det är en allmän konstant.

En annan observation som kan göras är att för A = -4 och B = 6 erhålls samma linje, trots att deras allmänna ekvation är annorlunda. I detta fall är den allmänna ekvationen -4x + 6y + C = 0.

Finns det andra sätt att hitta linjens allmänna ekvation?

Svaret är ja. Om lutningen på en linje är känd finns det, förutom den föregående, två sätt att hitta den allmänna ekvationen.

För detta används Point-Slope-ekvationen och Shear-Slope-ekvationen..

-Point-Slope-ekvationen: om m är lutningen på en linje och P = (x0, y0) en punkt genom vilken den passerar, så kallas ekvationen y-y0 = m (x-x0) Point-Slope-ekvationen.

-Shear-Slope-ekvationen: om m är lutningen på en linje och (0, b) är linjens skärning med Y-axeln, så kallas ekvationen y = mx + b Shear-Slope-ekvationen.

Med det första fallet erhålls att Point-Slope-ekvationen för en linje vars lutning är 2/3 ges av uttrycket y-y0 = (2/3) (x-x0).

För att komma till den allmänna ekvationen, multiplicera med 3 på båda sidor och alla termer är grupperade på ena sidan av likheten, med vilken man erhåller att -2x + 3y + (2 × 0-3y0) = 0 är den allmänna ekvationen av linjen, där C = 2 × 0-3y0.

Om det andra fallet används erhålls att ekvationen Cut-Slope för en linje vars lutning är 2/3 är y = (2/3) x + b.

Återigen, multiplicera med 3 på båda sidor och gruppera alla variabler, får vi -2x + 3y-3b = 0. Det senare är den allmänna ekvationen för linjen där C = -3b.

Faktiskt, när man tittar noga på båda fallen kan man se att det andra fallet helt enkelt är ett särskilt fall av det första (när x0 = 0).

Referenser

1. Fleming, W., & Varberg, D. E. (1989). Precalculus matematik. Prentice Hall PTR.
2. Fleming, W., & Varberg, D. E. (1989). Precalculus matematik: ett problemlösningstillvägagångssätt (2, Illustrerad utgåva). Michigan: Prentice Hall.
3. Kishan, H. (2005). Integral Calculus. Atlantic Publishers & Distributors.
4. Larson, R. (2010). Precalculus (8 utgåva). Cengage Learning.
5. Leal, J. M., & Viloria, N. G. (2005). Plans analytisk geometri. Mérida - Venezuela: Ledare Venezolana C. A.
6. Pérez, C. D. (2006). Förberäkning. Pearson Education.
7. Saenz, J. (2005). Differential Calculus med tidiga transcendenta funktioner för vetenskap och teknik (Andra upplagan utgåva). Hypotenusa.
8. Sullivan, M. (1997). Förberäkning. Pearson Education.