
Translationsjämviktstillstånd, exempel, övningar
Ett objekt påstås vara i translationell jämvikt när summan av krafterna som verkar på den är noll. Detta betyder inte att det nödvändigtvis finns vila, men rörelsen, om den existerar, skulle vara enhetlig rätlinjig eller uteslutande roterande, när det gäller ett stort föremål..
Villkoren för mekanisk jämvikt är baserade på Newtons mekaniklagar. Den första lagen säger oss faktiskt att ett objekt vilar eller rör sig med enhetlig rätlinjig rörelse MRU, förutsatt att ingen nettokraft verkar på det.

Nu är nettokraften eller den resulterande kraften helt enkelt vektorsumman av alla krafter som verkar på objektet. Enligt Newtons andra lag måste denna summa vara lika med produkten mellan massan och accelerationen, men om objektet inte accelereras försvinner denna summa.
Och i avsaknad av acceleration finns de två ovannämnda möjligheterna: kroppen är i vila, det vill säga den rör sig inte, eller om den gör det måste den vara med MRU. I det första fallet talar vi om statisk transnational jämvikt, och i det andra dynamiska.
Translationsjämvikt är en viktig faktor i många tekniska aspekter, till exempel inom konstruktion. Elementen som utgör en byggnad: balkar, kablar, ramar och mer måste vara i balans för att garantera stabiliteten i höljet.
Translationsbalans eftersträvas också i mobila strukturer, som rulltrappor, transportband och vid utövandet av många sporter..
Artikelindex
- 1 Villkor för translationell jämvikt
- 1.1 Diagram över fria kroppar
- 2 Exempel på translationell jämvikt
- 2.1 Byggnader och vägar
- 2.2 Böcker och föremål i hyllor
- 2.3 Möblerna
- 2.4 Trafikljus
- 2.5 Allmän belysning
- 3 Övningen löst
- 3.1 Lösning
- 4 Referenser
Translationsjämviktstillstånd
Antag att flera krafter verkar på en kropp, vilket vi betecknar som F1, Ftvå, F3... . Fn, med fetstil för att markera det faktum att krafter är vektorer och måste läggas till som sådana.
Vektorsumman för alla dessa krafter kallas resulterande kraft eller nettokraft. Om denna summering resulterar i nollvektorn är villkoret för translationell jämvikt uppfyllt:
F1+ Ftvå+ F3... .+ Fn = 0
Detta villkor kan skrivas kompakt med summeringsnotation:
∑ Fi = 0
När det gäller komponenterna i den resulterande kraften kan ovanstående ekvation, som är vektor, delas upp i tre skalära ekvationer, en för varje komponent i den resulterande kraften:
∑ Fix = 0; ∑ FY = 0 och ∑ Fz = 0
I praktiken är det inte lätt att eliminera summan av krafter, eftersom friktion är en kontaktkraft mellan ytor som knappast helt avbryts av någon annan kraft..
Detta är anledningen till att verkliga föremål nästan aldrig är undantagna från yttre krafter, och det är därför svårt att få translationell jämvikt.
Så ingenjörer använder mekanismer för att minska friktionen, till exempel lager och användning av smörjoljor..
Frikroppsdiagram
Frikroppsdiagrammet är ett diagram där de krafter som verkar på kroppen ritas. När man söker translationell jämvikt måste dessa krafter balanseras. Till exempel, om en vertikal kraft riktad nedåt verkar, såsom vikt, måste det finnas en uppåt vertikal kraft som har exakt samma storlek.
Denna kraft kan levereras av handen som stöder objektet så att det inte faller, ett rep eller helt enkelt bordets yta.
Om det finns en kraft som är tangentiell mot ytan, såsom kinetisk eller statisk friktion, måste det finnas en annan motsatt kraft för att balans ska existera. Låt oss till exempel titta på vikten som hänger från strängarna som visas i följande bild.
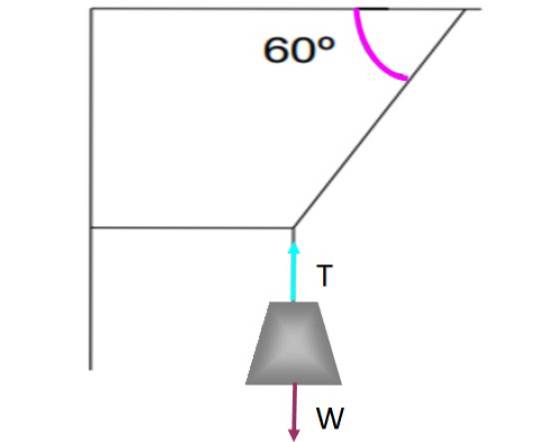
Tyngden hålls i translationell balans och utan att röra sig tack vare det vertikala repet som håller det genom att utöva en spänning T som kompenserar för vikten W. Varje kraft har representerats på vikten av en pil, var och en av samma storlek och med samma riktning, men motsatt riktning..
Balanseringskraften
Antag att en uppsättning krafter verkar på ett objekt. Detta kallas a kraftsystem varifrån den resulterande kan hittas såsom förklarats ovan: genom vektortillsättning av var och en av systemets krafter.
Tja, den motsatta kraften till denna resulterande kallas balanseringskraft. Om den resulterande kraften är FR och balanseringskraften är OCH, sedan:
OCH + FR = 0
Därför:
OCH = - FR
Exempel på translationell jämvikt
Många föremål som vi hittar dagligen, inom och utanför hemmet, är i translationell jämvikt:
Byggnader och vägar
Byggnader och vägar är byggda för att förbli stabila och inte välta eller kollapsa. Men i skyskrapor och i allmänhet mycket höga byggnader är viss flexibilitet nödvändig för att motstå vindens verkan..
Böcker och föremål i hyllor
Böcker i ett bibliotek och produkter i butikshyllorna är föremål som förblir i translationell jämvikt och inte rör sig..
Möblerna
Möblerna, platt-TV: n och bilderna på väggen, samt lamporna som hänger i taket, för att nämna några föremål, är i translationell balans..
Trafikljus
Trafikljusen är fästa med stolpar och kablar så att de inte faller. Ändå vet vi att vinden får dem att svänga.
Allmän belysning
Gatlyktorna är också i translationell balans, fixerade på lampstolparna, som gatubelysningen i huvudbilden..
Övningen löst
Hur stor måste kraften Fs med statisk friktion så att lådan i figuren förblir i vila mitt i det lutande planet i en vinkel α på 37º? Lådans massa är m = 8 kg.
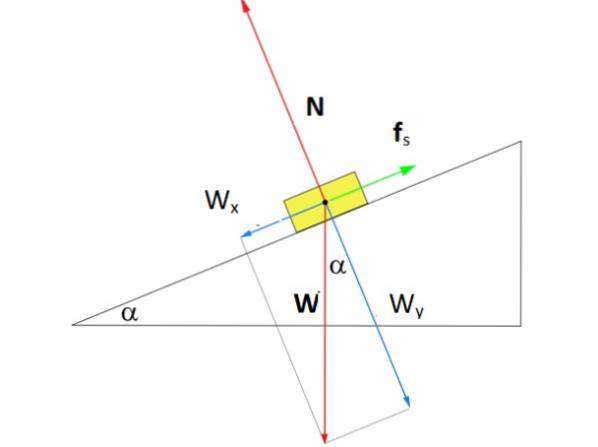
Lösning
Bilden visar frikroppsdiagrammet för lådan på planet. Det finns tre krafter som verkar på det: vikt W, riktad vertikalt nedåt, det normala N, vilket är den vinkelräta kraften som utövas av ytan på planet på lådan och slutligen den statiska friktionskraften Fs som är emot att lådan glider nedåt.
Det translationella jämviktsförhållandet säger att:
W + N + Fs = 0
Men vi måste komma ihåg att detta är en vektorsumma och för att genomföra det är det nödvändigt att bryta ner krafterna i komponenter längs koordinataxlarna.
I figuren har ett koordinatsystem ritats där x-axeln löper parallellt med ytan på det lutande planet. Med detta val faller den statiska friktionen på nämnda axel, medan det normala är på y-axeln. Vikt är den enda kraften som lutar och måste brytas ned med hjälp av trigonometri:
Wx = W. sin α
WY = W. cos α
Summan av krafter längs varje axel är:
∑ FY = N - WY = 0
∑ Fx = fs - Wx = 0
Av denna sista ekvation följer att:
Fs = Wx
Och som Wx = W. sin α och vikten i sin tur är W = m.g, där g är gravitationens värde, då är storleken på den statiska friktionen helt enkelt:
Fs = m⋅g⋅sen α = 8 kg × 9,8 m / stvå × sin 37º = 47,2 N.
Referenser
- Bauer, W. 2011. Fysik för teknik och vetenskap. Volym 1. Mc Graw Hill.
- Figueroa, D. (2005). Serie: Fysik för vetenskap och teknik. Volym 2. Dynamik. Redigerad av Douglas Figueroa (USB).
- Giambattista, A. 2010. Fysik. 2: a. Ed McGraw Hill.
- Serway, R., Jewett, J. (2008). Fysik för naturvetenskap och teknik. Volym 1. 7mamma. Ed. Cengage Learning.
- Tippens, P. 2011. Fysik: begrepp och tillämpningar. 7: e upplagan. Mcgraw hill.



Ingen har kommenterat den här artikeln än.