Konvex spegelkoncept, egenskaper, exempel

De konvex spegel eller divergerande är en böjd spegel, nästan alltid sfärisk i form och med den reflekterande ytan på sfärens yttre sida, såsom julgranens ornament. Tack vare konvexa speglar är det möjligt att uppnå ett stort antal bilder beroende på var objektet ligger och det är anledningen till att de har så många användningsområden.

Till exempel är speglarna som placeras på gatorna för att underlätta transitering av fordon i smala korsningar konvexa, eftersom de ger en bild med ett brett synfält.

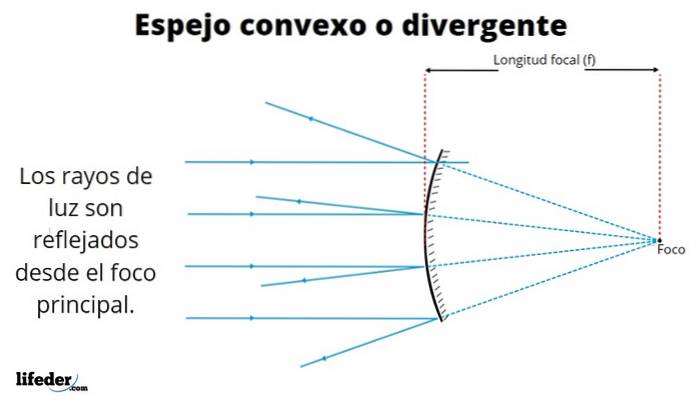
Bilderna som sålunda bildas är olika beroende på platsen där objektet placeras. Bilden ovan visar de parallella strålarna från en avlägsen källa som solen..

Strålarna reflekteras enligt reflektionslagen, vilket indikerar att strålens infallsvinkel är densamma som den reflekteras med. Som vi kan se separerar de reflekterade strålarna - de korsar inte - när de lämnar den speglande ytan, varför denna typ av spegel också kallas avvikande.

När reflektionerna sträcker sig bakom spegeln - streckade linjer i figuren - korsas de vid en punkt F som kallas fokus..

Artikelindex

• 1 Egenskaper för konvexa speglar
• 2 Bildbildning i den konvexa spegeln
• 3 Exempel och tillämpningar
  • 3.1 Speglar för att förhindra trafikolyckor
  • 3.2 Speglar för övervakning
  • 3.3 Backspeglar
  • 3.4 Cassegrain-teleskop
• 4 Ekvationer av den konvexa spegeln
  • 4.1 Förstoring av spegeln
  • 4.2 Förhållandet mellan objektet och dess bild i den konvexa spegeln
• 5 Intressanta ämnen
• 6 Referenser

Funktioner av konvexa speglar

Den konvexa spegeln har följande egenskaper (se bilden ovan):

-Spegelns anmärkningsvärda punkter är:

• C centrum, som sammanfaller med mitten av sfären som spegeln tillhör.
• F fokus, där strålarna reflekteras bakom spegeln konvergerar.
• Dess toppunkt P, som motsvarar mitten av den sfäriska ytan och är i linje med C och F.

-Ha optisk axel eller huvudaxel, vilken är linjen vinkelrät mot den spekulära ytan. Strålar som träffar bara den optiska axeln reflekteras i samma riktning.

-Mitten av sfären som spegeln tillhör är vid punkt C och r är dess radie. A C är känd som krökningscentrum, medan r Är han Krökningsradie och anger hur böjd spegeln är: den mindre r, mer accentuerad är den konvexa formen.

-Skärningspunkten för de reflekterade strålarna är känd som Brännpunkt av spegeln. Avståndet mellan F och P är ungefär r/två:

f = r / 2

Detta uttryck gäller för speglar vars storlek är mycket mindre än deras krökningsradie.

-Bilden som bildas är mindre och också virtuell eftersom den ligger bakom spegeln, som vi kommer att se nedan..

Bildbildning i den konvexa spegeln

För att veta vad bilden bildas i den konvexa spegeln används strålbehandling som består av att representera ljusstrålarna som lämnar objektet med raka linjer.

Dessa strålar reflekteras på spegelytan och de reflekterade strålarna ritas också. Strålmetoden är tillämplig på alla typer av speglar, inte bara konvexa.

Genom att förlänga de reflekterade strålarna skär de vid en viss punkt, och det är just där bilden bildas. Förlängningarna av de reflekterade strålarna som kommer från ett utsträckt föremål som ett träd visas i figuren nedan med streckade linjer.

I figuren nedan dras tre strålar från objektet, mycket speciella och lätta att rita, liksom deras reflektioner:

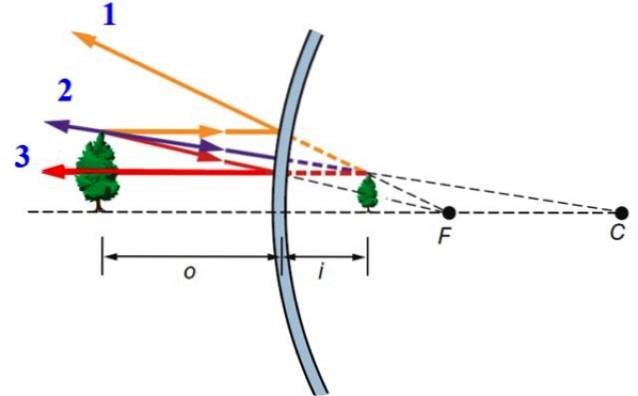
-Stråle 1, infallande parallellt med den optiska axeln.

-Stråle 2, som faller på ett sådant sätt att förlängningen av den reflekterade strålen passerar exakt genom spegelns fokus, det vill säga punkt F. Denna stråle reflekteras i en riktning parallell med den optiska axeln.

-Slutligen stråle 3, som kommer vinkelrätt mot den sfäriska ytan och av denna anledning reflekteras i samma riktning.

I princip tillämpas denna procedur på varje punkt i trädet, men med den information som erhålls från de tre strålarna som dras är det tillräckligt att hitta bilden av föremålet: den bildas bakom spegeln, den är rak och mindre original-.

Exempel och tillämpningar

Många högpolerade sfäriska ytor fungerar som konvexa speglar, till exempel glänsande och silverjulpynt samt glänsande nya stålskedar.

Även konvexa speglar har många praktiska tillämpningar, till exempel:

Speglar för att förhindra trafikolyckor

Konvexa speglar på gator och vägar hjälper till att förhindra olyckor, eftersom de gör att du kan se trafik från hörn.

Speglar för övervakning

Konvexa speglar används ofta i butiker och banker för att upptäcka tjuvar, samt för att undvika kollisioner mellan människor och gaffeltruckar som går genom gångar och mellan hyllor..

Backspeglar

Bilar och motorcyklar har konvexa backspeglar som ger lite mindre bilder men täcker mer synfält än platta speglar..

Cassegrain-teleskop

En av speglarna i det Cassegrain-reflekterande teleskopet, den sekundära spegeln, är konvex, även om den inte är sfärisk och tjänar till att reflektera bilden mot teleskopets huvudspegel..

Konvexa spegelekvationer

Låt oss betrakta de rätta trianglarna i följande figur, bestämd av stråle 1, som kommer från pilens topp, dess reflektion och dess förlängning.

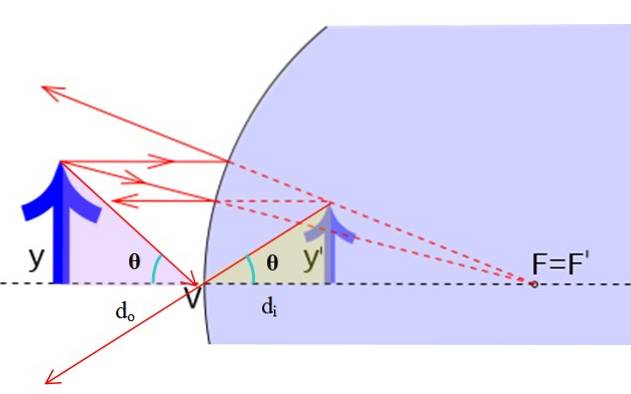
Originalbilden har höjden y, medan höjden på den virtuella bilden är y ' . Är det sant att:

tan θ = y / d_eller = y '/ d_i

Spegelförstoring

Förhållandet mellan höjden på bilden och objektets höjd är spegelförstoring, vilket kallas det, även om den erhållna bilden är mindre än det verkliga objektet. Vi betecknar det med m:

m = y '/ y = d_i / d_eller

Förhållandet mellan objektet och dess bild i den konvexa spegeln

Låt oss nu överväga denna andra figur, där AVF-regionen ungefär kan betraktas som en rätt triangel, eftersom spegelns krökning inte är särskilt accentuerad. Därför:

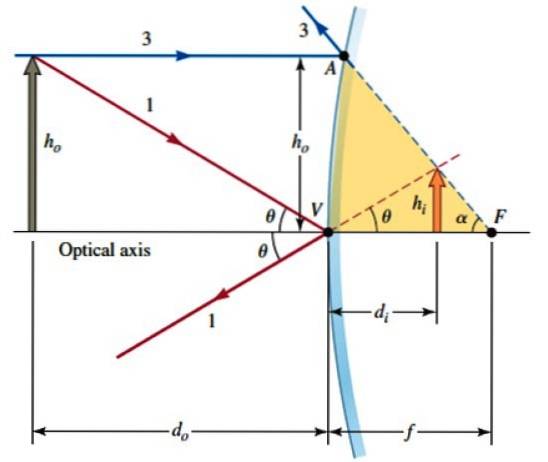
AV ≈ h_eller

Sedan:

tan α = h

1- (d_i / f) = d_i / d_eller

Genom att dela allt med d_i:

Därför, som F Y d_i är bakom spegeln placeras ett minustecken framför dem, medan för avstånd d_eller det är inte nödvändigt, eftersom det är framför spegeln. Således är den tidigare ekvationen:

Teman av intresse

Konkav spegel.

Referenser

1. Bauer, W. 2011. Fysik för teknik och vetenskap. Volym 2. Mc Graw Hill.
2. Giambattista, A. 2010. Fysik. 2: a. Ed McGraw Hill.
3. Katz, D. 2017. Fysik för forskare och ingenjörer. Cengage Learning.
4. Thomas, W. 2008. Konceptuell fysik. Mcgraw hill.
5. Tippens, P. 2011. Fysik: begrepp och tillämpningar. 7: e upplagan. Mcgraw hill.