
Volymflöde
Vad är volymflöde?
De volymflöde den gör det möjligt att bestämma vätskevolymen som passerar genom en sektion av ledningen och ger ett mått på hastigheten med vilken vätskan rör sig genom den. Därför är dess mätning särskilt intressant inom så olika områden som industri, medicin, konstruktion och forskning..
Att mäta en vätskas hastighet (vare sig det är en vätska, en gas eller en blandning av båda) är dock inte så enkelt som att mäta förflyttningshastigheten för en fast kropp. Därför händer det att för att känna till vätskans hastighet är det nödvändigt att känna till dess flöde.
Detta och många andra frågor relaterade till vätskor hanteras av den fysikgren som kallas vätskemekanik. Flöde definieras som hur mycket vätska som passerar genom en sektion av en ledning, vare sig det är en rörledning, en oljeledning, en flod, en kanal, en blodledning, etc., med beaktande av en tidsenhet.
Volymen som passerar genom ett givet område under en tidsenhet beräknas vanligtvis, även kallat volymflöde. Massan eller massflödet som passerar genom ett visst område vid en viss tidpunkt definieras också, även om det används mindre ofta än volymflödet..
Hur beräknas volymflödet?
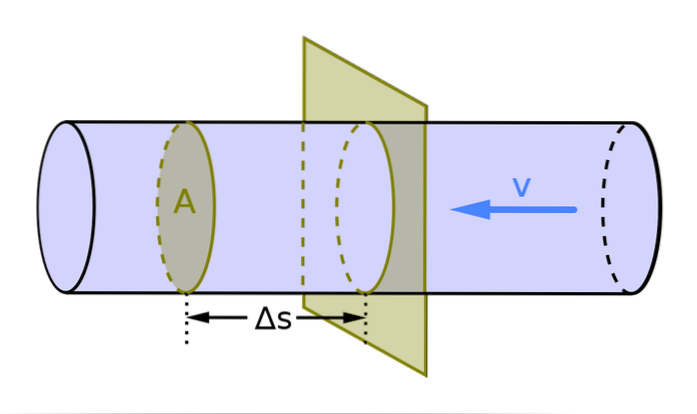
Volymflödet representeras av bokstaven Q. För de fall där flödet rör sig vinkelrätt mot ledarsektionen bestäms det med följande formel:
Q = A = V / t
I denna formel är A sektionen av ledaren (det är medelhastigheten för vätskan), V är volymen och t är tiden. Eftersom det internationella systemet mäter ledarens area eller sektion i mtvå och hastigheten i m / s mäts flödet m3/ s.
För de fall där hastigheten för fluidförskjutningen skapar en vinkel θ med riktningen vinkelrät mot ytsektionen A, är uttrycket för att bestämma flödeshastigheten följande:
Q = A cos θ
Detta överensstämmer med den föregående ekvationen, eftersom när flödet är vinkelrätt mot området A, är θ = 0 och därför cos θ = 1.
Ovanstående ekvationer är bara sanna om vätskans hastighet är likformig och om sektionens area är plan. I annat fall beräknas volymflödet genom följande integral:
Q = ∫∫s v d S
I denna integrerade dS är ytvektorn, bestämd av följande uttryck:
dS = n dS
Där är n enhetsvektorn normal mot kanalytan och dS är ett ytdifferentialelement.
Kontinuitetsekvation
Ett kännetecken för okomprimerbara vätskor är att vätskans massa konserveras med hjälp av två sektioner. Av denna anledning är kontinuitetsekvationen nöjd, vilket etablerar följande förhållande:
ρ1 TILL1 V1 = ρtvå TILLtvå Vtvå
I denna ekvation är ρ vätskans densitet.
För fall av regimer i permanent flöde, där densiteten är konstant och därför är det sant att ρ1 = ρtvå, kokar ner till följande uttryck:
TILL1 V1 = Atvå Vtvå
Detta motsvarar att bekräfta att flödet bevaras och därför:
F1 = Qtvå.
Av observationen av ovanstående följer att vätskor accelererar när de når en smalare del av en ledning, medan de saktar ner när de når en bredare del av en ledning. Detta faktum har intressanta praktiska tillämpningar, eftersom det gör det möjligt att spela med en vätskes rörelsehastighet.
Bernoullis princip
Bernoullis princip bestämmer att för en ideal vätska (det vill säga en vätska som varken har viskositet eller friktion) som rör sig i cirkulation genom en sluten ledning, förblir dess energi konstant under hela förskjutningen..
I slutändan är Bernoullis princip inget annat än formuleringen av lagen om energibesparing för flöde av en vätska. Bernoullis ekvation kan således formuleras enligt följande:
h + vtvå / 2g + P / ρg = konstant
I denna ekvation är h höjden och g är accelerationen på grund av tyngdkraften.
Bernoulli-ekvationen tar hänsyn till energin i en vätska när som helst, en energi som består av tre komponenter.
- En kinetisk komponent som innehåller energi på grund av hastigheten med vilken vätskan rör sig.
- En komponent genererad av gravitationspotentialen som en följd av höjden vid vilken vätskan är.
- En komponent av flödesenergi, vilket är den energi en vätska har på grund av tryck.
I det här fallet uttrycks Bernoullis ekvation enligt följande:
h ρ g + (vtvå ρ) / 2 + P = konstant
I fallet med en riktig vätska uppfylls inte uttrycket för Bernoulli-ekvationen logiskt, eftersom friktionsförluster uppstår i fluidförskjutningen och det är nödvändigt att tillgripa en mer komplex ekvation.
Vad påverkar volymflödet?
Volymflödet påverkas om det finns ett hinder i kanalen.
Dessutom kan volymflödeshastigheten också förändras på grund av variationer i temperatur och tryck i den verkliga vätskan som rör sig genom en ledning, speciellt om detta är en gas, eftersom volymen som en gas upptar varierar som en funktion av temperaturen och trycket på.
Enkel metod för att mäta volymflöde
En riktigt enkel metod för att mäta volymflödet är att låta en vätska strömma in i en doseringstank under en viss tidsperiod..
Denna metod är i allmänhet inte särskilt praktisk, men sanningen är att det är extremt enkelt och mycket illustrativt att förstå innebörden och vikten av att känna till en vätskeflödeshastighet..
På detta sätt tillåts vätskan att strömma in i en mätbehållare under en tidsperiod, den ackumulerade volymen mäts och det erhållna resultatet divideras med förfluten tid.
Referenser
- Flöde (vätska) (n.d.). På Wikipedia. Återställd från es.wikipedia.org.
- Volymflöde (n.d.). På Wikipedia. Återställd från en.wikipedia.org.
- Engineers Edge, LLC. "Fluid Volumetric Flow Rate Equation". Engineers Edge
- Mott, Robert (1996). "1". Tillämpad vätskemekanik (4: e upplagan). Mexiko: Pearson Education.
- Batchelor, G.K. (1967). En introduktion till vätskedynamik. Cambridge University Press.
- Landau, L.D. Lifshitz, E.M. (1987). Flytande mekanik. Kurs för teoretisk fysik (2: a upplagan). Pergamon Press.

Ingen har kommenterat den här artikeln än.