
Definition av övervakningsfunktion, egenskaper, exempel
A förväntningsfunktion är ett förhållande där varje element som tillhör kodmenyn är en bild av minst ett element i domänen. Även känd som funktion på, ingår i klassificeringen av funktioner med avseende på hur deras element är relaterade.
Till exempel en funktion F: A → B definieras av F (x) = 2x
Som lyder "F vad sägs om TILL fram tills B definieras av F (x) = 2x "
Det är dags att definiera start- och finishuppsättningarna A och B.
A: 1, 2, 3, 4, 5 Nu visar värdena eller bilderna som vart och ett av dessa element visas när de utvärderas i F, kommer att vara elementen i koddomen.
F (1) = 2
F (2) = 4
F (3) = 6
F (4) = 8
F (5) = 10
Således bildar helheten B: 2, 4, 6, 8, 10
Man kan då dra slutsatsen att:
F: 1, 2, 3, 4, 5 → 2, 4, 6, 8, 10 definieras av F (x) = 2x Det är en förväntningsfunktion
Varje element i kodmenyn måste vara resultatet av minst en operation av den oberoende variabeln genom funktionen i fråga. Det finns ingen begränsning av bilder, ett element i kodmenyn kan vara en bild av mer än ett element i domänen och fortfarande försöker en förväntningsfunktion.
Bilden visar två exempel med förväntade funktioner.
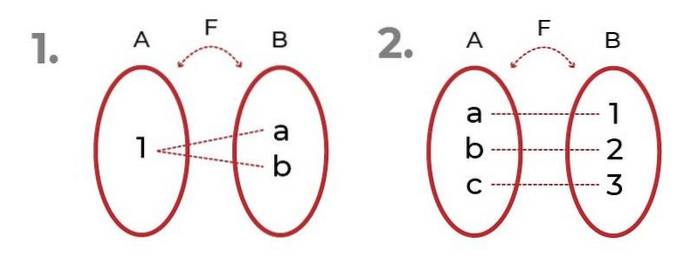
I det första observeras att bilderna kan hänvisas till samma element utan att kompromissa med surjectivity av funktionen.
I den andra ser vi en rättvis fördelning mellan domän och bilder. Detta ger upphov till bijektiv funktion, där kriterierna för injektionsfunktion och surjectivfunktion.
En annan metod för att identifiera förväntade funktioner, är att kontrollera om kodmenyn är lika med funktionsomfånget. Detta innebär att om ankomstuppsättningen är lika med bilderna som tillhandahålls av funktionen vid utvärdering av den oberoende variabeln, funktionen är förväntad.
Artikelindex
- 1 Fastigheter
- 1.1 Funktionskonditionering
- 2 Exempel: lösta övningar
- 2.1 Övning 1
- 2.2 Övning 2
- 2.3 Övning 3
- 2.4 Övning 4
- 2.5 Övning 4
- 2.6 Övning 5
- 3 Föreslagna övningar
- 4 Referenser
Egenskaper
Att överväga förväntningar till en funktion måste följande uppfyllas:
Vara F: DF → CF
∀ b ℮ CF OCH till ℮ DF / F (a) = b
Detta är det algebraiska sättet att fastställa det för alla "b" som tillhör CF det finns ett “a” som tillhör DF så att funktionen F utvärderad i "a" är lika med "b".
Surjektivitet är en egenart hos funktioner, där kodmenyn och intervallet liknar varandra. Således utgör elementen som utvärderas i funktionen ankomstuppsättningen.
Funktionskonditionering
Ibland en funktion som inte är det förväntningar, det kan utsättas för vissa villkor. Dessa nya villkor kan göra det till en förväntningsfunktion.
Alla typer av modifieringar av funktionens domän och kodnamn är giltiga, där målet är att uppfylla surjektivitetsegenskaperna i motsvarande relation.
Exempel: övningar lösta
För att uppfylla villkoren för surjectivity olika konditioneringstekniker måste tillämpas, detta för att säkerställa att varje element i kodmenyn ligger inom bilduppsättningen av funktionen.
Övning 1
- Låt funktionen F: R → R definieras av linjen F (x) = 8 - x
A: [Alla verkliga siffror]
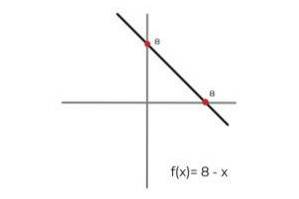
I det här fallet beskriver funktionen en kontinuerlig linje som täcker alla reella tal i både dess domän och intervall. Eftersom funktionsomfånget RF motsvarar codomain R Man kan dra slutsatsen att:
F: R → R definieras av linjen F (x) = 8 - x är en förväntningsfunktion.
Detta gäller för alla linjära funktioner (funktioner vars största variabel är en).
Övning 2
- Studera funktionen F: R → R definieras av F (x) = xtvå : Definiera om det är en förväntningsfunktion. Om inte, visa villkoren som är nödvändiga för att göra det förväntat.
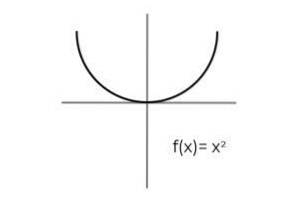
Det första du bör tänka på är codomainen till F, som består av de verkliga siffrorna R. Det finns inget sätt för funktionen att returnera negativa värden, vilket utesluter de verkliga negativen från de möjliga bilderna.
Konditionering av codainen till intervallet [0 , ∞ ]. Det undviks att lämna delar av kodmoden oberoende igenom F.
Bilderna upprepas för par av element av den oberoende variabeln, t.ex. x = 1 Y x = - 1. Men detta påverkar bara injektivitet av funktionen, inte är ett problem för denna studie.
På detta sätt kan man dra slutsatsen att:
F: R →[0, ∞ ) definieras av F (x) = xtvå Det är en förväntningsfunktion
Övning 3
- Definiera villkoren för codomain som de skulle göra förväntningar till funktionerna
F: R → R definieras av F (x) = Sen (x)
F: R → R definieras av F (x) = Cos (x)
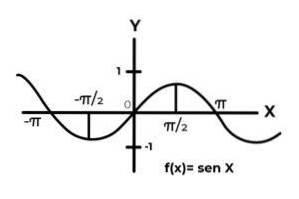
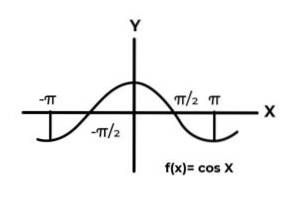
De trigonometriska funktionernas beteende liknar vågorna, vilket är mycket vanligt för att hitta repetitioner av den beroende variabeln mellan bilderna. I de flesta fall är funktionsomfånget begränsat till en eller flera sektorer i den verkliga linjen.
Detta är fallet med Sine- och Cosine-funktionerna. Där deras värden fluktuerar i intervallet [-1, 1]. Detta intervall måste konditionera kodens huvud för att uppnå funktionens överföringsförmåga.
F: R →[-elven] definieras av F (x) = Sen (x) Det är en förväntningsfunktion
F: R →[-elven]definieras av F (x) = Cos (x) Det är en förväntningsfunktion
Övning 4
- Studera funktionen
F: [0, ∞ ) → R definieras av F (x) = ± √x beteckna om det är en förväntningsfunktion
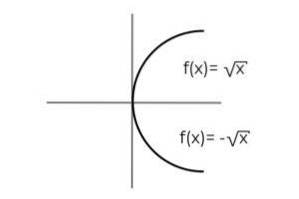
Funktionen F (x) = ± √x Det har det särdrag att det definierar två beroende variabler till varje värde av "x". Det vill säga intervallet tar emot två element för varje som görs i domänen. Ett positivt och negativt värde måste verifieras för varje värde av "x".
När man observerar startuppsättningen noteras det att domänen redan har begränsats, detta för att undvika de obestämmelser som produceras vid utvärdering av ett negativt tal inom en jämn rot.
Vid verifiering av funktionsomfånget noteras att varje värde på kodmoden tillhör intervallet.
På detta sätt kan man dra slutsatsen att:
F: [0, ∞ ) → R definieras av F (x) = ± √x Det är en förväntningsfunktion
Övning 4
- Studera funktionen F (x) = Ln x beteckna om det är en förväntningsfunktion. Konditionera ankomst- och avgångsuppsättningarna för att anpassa funktionen till surjectivity-kriterierna.
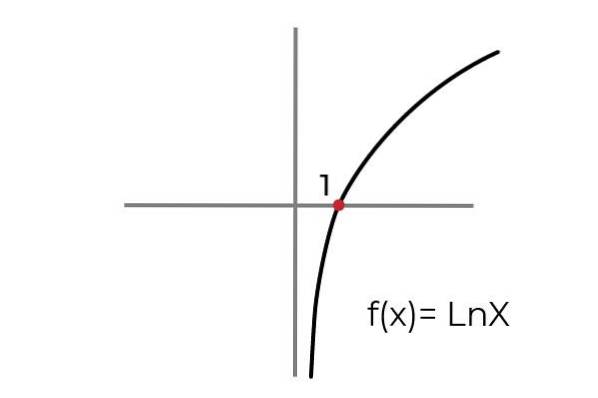
Som visas i diagrammet funktionen F (x) = Ln xden definieras för värden på "x" större än noll. Medan värdena "och" eller bilderna kan ta något verkligt värde.
På detta sätt kan vi begränsa domänen för F (x) = till intervall (0 , ∞ )
Så länge funktionsomfånget kan behållas som en uppsättning av reella tal R.
Med tanke på detta kan man dra slutsatsen att:
F: [0, ∞ ) → R definieras av F (x) = Ln x Det är en förväntningsfunktion
Övning 5
- Studera funktionen absolutvärde F (x) = | x | och ange ankomst- och avgångsuppsättningar som uppfyller kriterierna för surjektivitet.
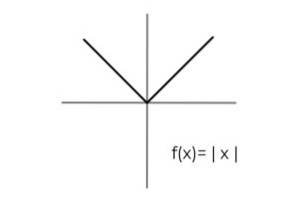
Funktionens domän gäller för alla reella tal R. På detta sätt måste den enda konditioneringen utföras i kodmen, med hänsyn till att absolutvärdesfunktionen endast tar positiva värden..
Vi fortsätter med att fastställa kodens huvudsakliga funktion som motsvarar den
[0 , ∞ )
Nu kan man dra slutsatsen att:
F: [0, ∞ ) → R definieras av F (x) = | x | Det är en förväntningsfunktion
Föreslagna övningar
- Kontrollera om följande funktioner är förväntade:
- F: (0, ∞ ) → R definieras av F (x) = Logg (x + 1)
- F: R → R definieras av F (x) = x3
- F: R →[1, ∞ ) definieras av F (x) = xtvå + 1
- [0, ∞ ) → R definieras av F (x) = Logg (2x + 3)
- F: R → R definieras av F (x) = Sek x
- F: R - 0 → R definieras av F (x) = 1 / x
Referenser
- Introduktion till logik och kritiskt tänkande. Merrilee H. lax. University of Pittsburgh
- Problem i matematisk analys. Piotr Biler, Alfred Witkowski. University of Wroclaw. Polen.
- Element av abstrakt analys. Mícheál O'Searcoid PhD. Institutionen för matematik. University College Dublin, Beldfield, Dublind 4
- Introduktion till logik och metoderna för deduktiva vetenskaper. Alfred Tarski, Oxford i New York. Oxford University press.
- Principer för matematisk analys. Enrique Linés Escardó. Ledare Reverté S. A 1991. Barcelona Spanien.


Ingen har kommenterat den här artikeln än.