
Idealisk gasmodell, beteende, exempel
A idealisk gas eller perfekt gas Det är en där den molekylära attraktionen eller avstötningskraften mellan partiklarna som komponerar den anses vara obetydlig, därför är all dess inre energi kinetisk, det vill säga energi associerad med rörelse.
I en sådan gas är partiklarna vanligtvis ganska långt ifrån varandra, även om de ibland kolliderar med varandra och med behållarens väggar..
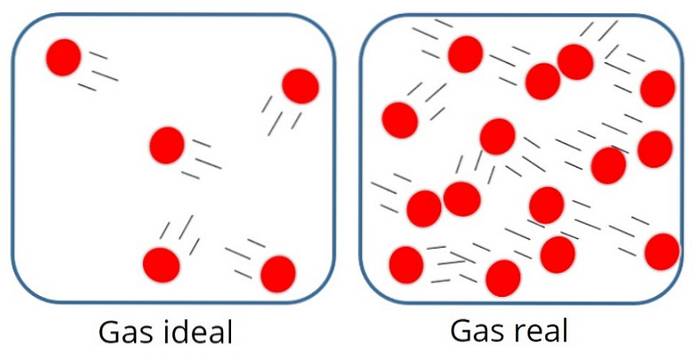
Å andra sidan, i den ideala gasen, har varken partiklarnas storlek eller massa betydelse, eftersom det antas att volymen som upptas av dem är mycket liten jämfört med gasens volym..
Detta är naturligtvis bara en approximation, för i verkligheten finns det alltid en viss grad av interaktion mellan atomer och molekyler. Vi vet också att partiklar upptar utrymme och har massa..
Dessa antaganden fungerar emellertid ganska bra i många fall, såsom gaser med låg molekylvikt, i ett bra tryck- och temperaturområde..
Men gaser med hög molekylvikt, speciellt vid höga tryck eller låga temperaturer, beter sig inte alls som ideala gaser och andra modeller som skapats i syfte att beskriva dem med större precision behövs..
Artikelindex
- 1 Första experiment
- 1.1 De ideala gaslagarna
- 2 Idealisk gasmodell
- 2.1 Idealisk gasekvation för tillstånd
- 2.2 Gaskonstanten
- 3 Uppförande av en idealgas
- 4 Exempel på ideala gaser
- 4.1 Ädelgaser
- 4.2 Luftballongen
- 4.3 Heliumballonger
- 5 Referenser
Första experiment
Lagarna som styr gaser är empiriska, det vill säga de härstammar från experiment. De mest anmärkningsvärda experimenten genomfördes under hela sjutton, arton och tidigt artonhundratalet.
Först är de av Robert Boyle (1627-1691) och Edme Mariotte (1620-1684), som oberoende ändrade Tryck i en gas och registrerade dess ändring av volym, att finna att de var omvänt proportionella: ju högre tryck desto mindre volym.

Jacques Charles (1746-1823) konstaterade för sin del att volymen och temperatur absoluta värden var direkt proportionella så länge trycket förblev konstant.
Amadeo Avogadro (1776-1856) upptäckte att två identiska volymer av olika gaser innehöll samma antal partiklar, så länge som tryck och temperatur var desamma. Och slutligen sa Joseph de Gay Lussac (1778-1850) att genom att hålla volymen fast är trycket i en gas direkt proportionellt mot temperaturen..
De ideala gaslagarna
Dessa upptäckter uttrycks i enkla formler, kallande sid att pressa, V till volym, n till antalet partiklar och T den ideala gastemperaturen:
Boyle-Mariotte lag
Så länge temperaturen är fixerad inträffar följande:
p⋅V = konstant
Charles Law
När gasen är under konstant tryck:
V / T = konstant
Gay Lussacs lag
Att hålla gasen på en fast volym är nöjd med att:
p / T = konstant
Avogadros lag
Identiska gasvolymer, under samma tryck och temperaturförhållanden, har samma antal partiklar. Därför kan vi skriva:
V ∝ n
Där n är antalet partiklar och ∝ är symbolen för proportionalitet.
Idealisk gasmodell
Den ideala gasmodellen beskriver en gas så att:
-När partiklarna interagerar, gör de det under en mycket kort tid, med hjälp av elastiska kollisioner, där momentum och kinetisk energi bevaras..
-Dess beståndsdelar är punktliga, med andra ord, deras diameter är mycket mindre än det genomsnittliga avståndet som de färdas mellan en kollision och en annan..
-Intermolekylära krafter finns inte.
-Kinetisk energi är proportionell mot temperaturen.
Monatomiska gaser - vars atomer inte är bundna ihop - och lågmolekylär vikt, under standardförhållanden för tryck och temperatur (atmosfärstryck och 0 ° C temperatur), har ett sådant beteende att den ideala gasmodellen är en mycket bra beskrivning för dem..
Idealisk gasekvation för tillstånd
De gaslagar som anges ovan kombinerar för att bilda den allmänna ekvationen som styr den ideala gasens beteende:
V ∝ n
V ∝ T
Därför:
V ∝ n⋅T
Från Boyles lag:
V = konstant / p
Så vi kan bekräfta att:
V = (konstant x n⋅T) / p
Konstanten kallas gaskonstant och betecknas med bokstaven R. Med detta val relaterar den ideala gasekvationen för tillstånd fyra variabler som beskriver gasens tillstånd, nämligen n, R, p och T, vilket lämnar:
p⋅V = n⋅R⋅T
Denna relativt enkla ekvation överensstämmer med de ideala gaslagarna. Till exempel, om temperaturen är konstant, minskar ekvationen till Boyle-Mariotte-lagen.
Gaskonstanten
Som vi har sagt tidigare, under standardförhållanden för temperatur och tryck, det vill säga vid 0 ° C (273,15 K) och en tryckatmosfär, är beteendet hos många gaser nära det för den ideala gasen. Under dessa förhållanden är volymen på 1 mol av gasen 22 414 liter.
Isåfall:
R = (p⋅V) / (n⋅T) = (1 atm x 22,414 L) / (1 mol x 273,15 K) = 0,0821 atm ⋅ L / mol ⋅ K
Gaskonstanten kan också uttryckas i andra enheter, till exempel i SI International System är det värt:
R = 8,314 J3 mol-1⋅ K-1
När man löser ett problem med den ideala gaslagen är det bekvämt att vara uppmärksam på de enheter där konstanten uttrycks, eftersom det finns många möjligheter som vi kan se.
Uppförande av en idealgas
Som vi har sagt uppför sig gas under standardförhållanden för tryck och temperatur och som har låg molekylvikt mycket nära den ideala gasen. Därför är ekvationen p⋅V = n⋅R⋅T användbar för att hitta förhållandet mellan de fyra variablerna som beskriver den: n, p, V och T.
På detta sätt kan vi föreställa oss en del idealgas som är innesluten i en behållare och bildad av små partiklar, som från tid till annan kolliderar med varandra och med behållarens väggar, alltid elastiskt..
Detta är vad vi ser i följande animering av en del helium, en monatomisk ädelgas:
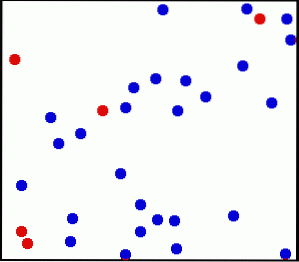
Exempel på ideala gaser
En idealgas är en hypotetisk gas, det vill säga det är en idealisering, men i praktiken beter sig många gaser på ett mycket nära sätt, vilket gör det möjligt för modellen p⋅V = n⋅R arroT att ge mycket bra resultat..
ädelgaser
Exempel på gaser som beter sig som idealiska under standardförhållanden är ädelgaser, liksom lätta gaser: väte, syre och kväve..
Den aerostatiska ballongen

Charles lag kan tillämpas på varmluftsballongen i figur 1: gasen värms upp, därför expanderar luften som fyller ballongen och som en konsekvens stiger den.
Heliumballonger
Helium är, tillsammans med väte, det vanligaste elementet i universum, och ändå är det sällsynt på jorden. Eftersom det är ädelgas är det inert, till skillnad från väte, det är därför heliumfyllda ballonger används i stor utsträckning som dekorativa element..
Referenser
- Atkins, P. 1999. Fysisk kemi. Omega-utgåvor.
- Chang, R. 2013. Kemi. 11: e. Utgåva. Mc Graw Hill utbildning.
- Cengel, Y. 2012. Termodynamik. 7: e upplagan. Mcgraw hill.
- Cimbala, C. 2006. Fluid Mechanics, Fundamentals and Applications. Mc. Graw hill.
- Giambattista, A. 2010. Fysik. 2: a. Ed McGraw Hill.


Ingen har kommenterat den här artikeln än.