Magnetiska induktionsformler, hur den beräknas och exempel

De magnetisk induktion eller magnetisk flödestäthet är en förändring av miljön orsakad av närvaron av elektriska strömmar. De ändrar naturen hos det utrymme som omger dem och skapar en landsbygden vektor.

Vektoren magnetisk induktion, magnetisk flödestäthet Eller bara magnetiskt fält B, den har tre särdrag: en intensitet uttryckt med ett numeriskt värde, en riktning och också en känsla som ges vid varje punkt i rymden. Det är markerat med fet stil för att skilja det från rent numeriska eller skalära kvantiteter.

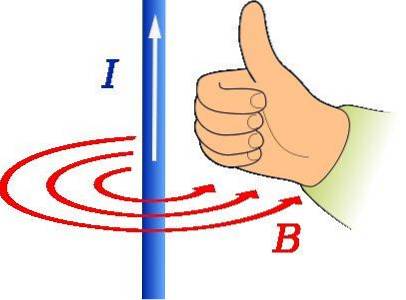
Höger tumregel används för att hitta riktningen och riktningen för magnetfältet som orsakas av en strömbärande tråd, som visas i figuren ovan.

Tummen på höger hand ska peka i strömriktningen. Rotationen av de fyra återstående fingrarna indikerar formen på B, som i figuren representeras av de koncentriska röda cirklarna.

I ett sådant fall är adressen till B är tangentiell för omkretsen koncentrisk med tråden och är moturs.

De magnetisk induktion B I det internationella systemet mäts Tesla (T), men det är oftare att mäta det i en annan enhet som heter Gauss (G). Båda enheterna namngavs respektive för att hedra Nikola Tesla (1856-1943) och Carl Friedrich Gauss (1777-1855) för deras extraordinära bidrag till vetenskapen om elektricitet och magnetism..

Artikelindex

• 1 Vilka egenskaper har magnetisk induktion eller magnetisk flödestäthet??
• 2 Biot-Savarts lag
• 3 formler
• 4 Hur beräknas det?
  • 4.1 Exempel
• 5 Referenser

Vilka egenskaper har magnetisk induktion eller magnetisk flödestäthet?

En kompass som placeras nära strömförande tråd kommer alltid att passa in B. Den danska fysikern Hans Christian Oersted (1777-1851) var den första som märkte detta fenomen i början av 1800-talet.

Och när strömmen upphör, pekar kompassen som alltid på geografisk norr. Genom att noggrant ändra kompassens position erhålls en karta över magnetfältets form.

Denna karta har alltid formen av cirklar koncentriska till tråden, som beskrivs i början. På detta sätt kan du visualisera B.

Även om tråden inte är rak, vektorn B den kommer att bilda koncentriska cirklar runt den. För att bestämma fältets form, föreställ dig bara mycket små trådsegment, så små att de verkar rätlinjiga och omges av koncentriska cirklar..

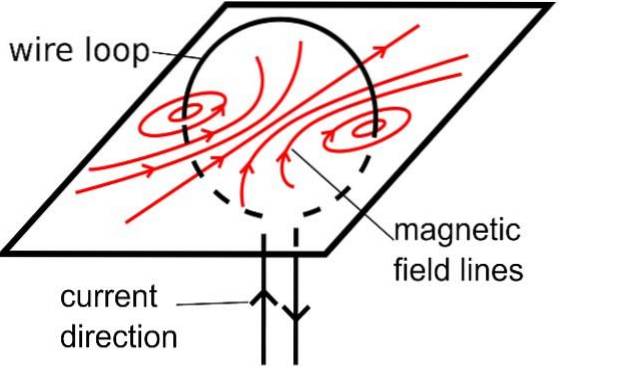
Detta pekar på en viktig egenskap hos magnetfältlinjer. B: de har ingen början eller slut, de är alltid slutna kurvor.

Biot-Savarts lag

1800-talet markerade början på tidsåldern för elektricitet och magnetism inom vetenskapen. Runt 1820 upptäckte de franska fysikerna Jean Marie Biot (1774-1862) och Felix Savart (1791-1841) lagen som bär deras namn och som gör att vi kan beräkna vektorn B.

De gjorde följande observationer om bidraget till magnetfältet som produceras av ett trådsegment med differentiell längd dl som bär en elektrisk ström Jag:

• Storleken på B minskar med den inversa kvadraten på avståndet till tråden (detta är vettigt: bort från tråden intensiteten på B måste vara mindre än nära punkter).
• Storleken på B är proportionell mot strömens intensitet Jag som går genom tråden.
• Adressen till B är tangentiellt för radieomkretsen r centrerad på tråden och känslan av B ges, som vi sa, genom regeln om höger tumme.

Korsprodukten eller korsprodukten är det lämpliga matematiska verktyget för att uttrycka den sista punkten. För att skapa en vektorprodukt behövs två vektorer som definieras enligt följande:

• dl är vektorn vars storlek är differenssegmentets längd dl
• r är vektorn som går från ledningen till den punkt där du vill hitta fältet

Formler

Allt detta kan kombineras till ett matematiskt uttryck:

Den konstanta proportionalitet som krävs för att upprätta jämställdhet är magnetisk permeabilitet av fritt utrymme μ_eller  = 4π.10^-7 T.m / A

Detta uttryck är Biot och Savart-lagen, som gör det möjligt för oss att beräkna magnetfältet för ett aktuellt segment.

Ett sådant segment måste i sin tur vara en del av en större och mer sluten krets: en strömfördelning.

Villkoret att kretsen är stängd är nödvändig för att en elektrisk ström ska kunna strömma. Elektrisk ström kan inte strömma i öppna kretsar.

Slutligen, för att hitta det totala magnetfältet för nämnda strömfördelning, läggs alla bidrag till varje differentiellt segment till dl. Detta motsvarar att integrera över hela distributionen:

För att tillämpa Biot-Savart-lagen och beräkna den magnetiska induktionsvektorn är det nödvändigt att överväga några mycket viktiga viktiga punkter:

• Korsprodukten mellan två vektorer resulterar alltid i en annan vektor.

• 

• Det är bekvämt att hitta vektorprodukten innan för att övergå till upplösningen av integralen löses integralen för var och en av de komponenter som erhålls separat.
• Det är nödvändigt att rita en bild av situationen och upprätta ett lämpligt koordinatsystem.
• Närhelst förekomsten av någon symmetri observeras, bör den användas för att spara beräkningstid.
• När det finns trianglar är Pythagoras sats och kosinosats till stor hjälp för att fastställa det geometriska förhållandet mellan variablerna.

Hur beräknas det?

Med ett praktiskt exempel på beräkning av B för en rak tråd gäller dessa rekommendationer.

Exempel

Beräkna magnetfältvektorn som en mycket lång rätlinjig tråd producerar vid en punkt P i rymden, enligt figuren som visas.

Från figuren måste du:

• Tråden riktas i vertikal riktning, med ström I som flyter uppåt. Denna riktning är + y i koordinatsystemet, vars ursprung är vid punkt O.

• 

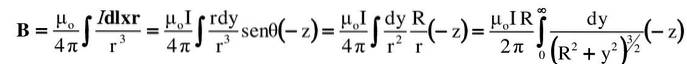
• I ett sådant fall, enligt regeln för höger tumme, B vid punkt P är den riktad mot pappersinsidan, det är därför den betecknas med en liten cirkel och ett "x" i figuren. Denna adress tas som -z.
• Den högra triangeln vars ben är Y Y R, relatera båda variablerna enligt Pythagoras sats: r^två= R^två+Y^två

Allt detta ersätts med integralen. Korsprodukten eller korset indikeras av dess storlek plus dess riktning och dess känsla:

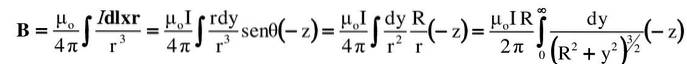
Den föreslagna integralen finns i en tabell över integraler eller löses genom en lämplig trigonometrisk ersättning (läsaren kan kontrollera resultatet med y = Rtg θ):

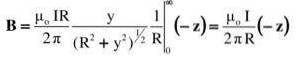
Resultatet överensstämmer med vad som förväntades: fältets storlek minskar med avståndet R och ökar proportionellt med intensiteten för strömmen I.

Även om en oändligt lång tråd är en idealisering är det erhållna uttrycket en mycket bra approximation för fältet för en lång tråd.

Med Biot och Savarts lag är det möjligt att hitta magnetfältet för andra mycket symmetriska fördelningar, såsom en cirkulär slinga som bär ström, eller böjda trådar som kombinerar rätlinjiga och krökta segment..

För att analytiskt kunna lösa den föreslagna integralen måste problemet naturligtvis ha en hög grad av symmetri. Annars är alternativet att lösa integralen numeriskt.

Referenser

1. Serway, R., Jewett, J. (2008). Fysik för naturvetenskap och teknik. Volym 2. Mexiko. Cengage Learning Editors. 367-372.