De Faradays lag i elektromagnetism säger att ett föränderligt magnetfältflöde kan inducera en elektrisk ström i en sluten krets.
1831 experimenterade den engelska fysikern Michael Faraday med rörliga ledare inom ett magnetfält och även olika magnetfält som passerade genom fasta ledare..
Faraday insåg att om han varierade magnetfältflödet över tiden kunde han skapa en spänning som var proportionell mot den variationen. Om ε är spänningen eller inducerad elektromotorisk kraft (inducerad emf) och Φ är magnetfältets flöde, i matematisk form kan det uttryckas:
| ε | = Aj / At
Där symbolen Δ anger variation av kvantiteten och staplarna i emf indikerar absolutvärdet för detta. Eftersom det är en sluten krets kan strömmen strömma i ena riktningen eller den andra.
Magnetiskt flöde, producerat av ett magnetfält över en yta, kan variera på ett antal sätt, till exempel:
-Flytta en stavmagnet genom en cirkulär slinga.
-Öka eller minska intensiteten hos magnetfältet som passerar genom slingan.
-Lämna fältet fast, men med hjälp av någon mekanism ändra området på slingan.
-Kombinera ovanstående metoder.
Artikelindex
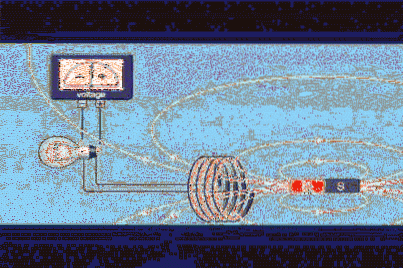
Antag att du har en sluten krets av område A, till exempel en cirkulär slinga eller lindning lika med den i figur 1, och att du har en magnet som producerar ett magnetfält B.
Magnetfältflödet Φ är en skalär kvantitet som hänvisar till antalet fältlinjer som passerar område A. I figur 1 är de vita linjerna som lämnar magnetens nordpol och återgår genom söder..
Fältets intensitet kommer att vara proportionell mot antalet linjer per ytenhet, så vi kan se att det vid polerna är mycket intensivt. Men vi kan ha ett mycket intensivt fält som inte producerar flöde i slingan, vilket vi kan uppnå genom att ändra orienteringen på detta (eller magneten).
För att ta hänsyn till orienteringsfaktorn definieras magnetfältflödet som den skalära produkten mellan B Y n, varelse n enhetens normala vektor mot slingans yta och som indikerar dess orientering:
Φ = B•n A = BA.cosθ
Där θ är vinkeln mellan B Y n. Om till exempel B Y n är vinkelräta är magnetfältflödet noll, för i så fall är fältet tangent till slingans plan och kan inte passera genom dess yta.
Istället ja B Y n är parallella betyder det att fältet är vinkelrätt mot slingans plan och linjerna passerar genom det så långt som möjligt.
Enheten i det internationella systemet för F är webber (W), där 1 W = 1 T.mtvå (läs "tesla per kvadratmeter").
I figur 1 kan vi se att spänningens polaritet ändras när magneten rör sig. Polariteten fastställs av Lenzs lag, som säger att den inducerade spänningen måste motsätta sig variationen som producerar den.
Om till exempel det magnetiska flöde som produceras av magneten ökar, upprättas en ström i ledaren som cirkulerar och skapar sitt eget flöde, vilket motsätter sig denna ökning..
Om tvärtom det flöde som skapas av magneten minskar cirkulerar den inducerade strömmen på ett sådant sätt att dess eget flöde motverkar nämnda minskning..
För att ta hänsyn till detta fenomen placeras ett negativt tecken före Faradays lag och det är inte längre nödvändigt att placera de absoluta värdet staplar:
e = -Aj / At
Detta är Faraday-Lenz-lagen. Om flödesvariationen är oändlig, ersätts deltorna med differentier:
e = -d2 / dt
Ovanstående ekvation är giltig för en slinga. Men om vi har en spole med N-varv är resultatet mycket bättre, eftersom EMF multipliceras N gånger:
ε = - N (dl / dt)
För att strömmen ska kunna slå på lampan som ska produceras måste det finnas relativ rörelse mellan magneten och slingan. Detta är ett av sätten på vilket flödet kan variera, för på detta sätt förändras fältets intensitet genom slingan..
Så snart magnetens rörelse upphör, slocknar lampan, även om magneten står stilla i mitten av öglan. Det som behövs för att cirkulera strömmen som tänder lampan är att fältflödet varierar.
När magnetfältet varierar med tiden kan vi uttrycka det som:
B = B (t).
Genom att hålla slingans område A konstant och låta det vara fixerat i en konstant vinkel, som för figuren är 0º, då:
Om det är möjligt att ändra slingans område, lämna orienteringen fast och placera den i mitten av ett konstant fält, ges den inducerade emk av:
Ett sätt att uppnå detta är att sätta en stång som glider på en ledarskena med en viss hastighet, som visas i följande bild.
Stången och skenan, plus en glödlampa eller ett motstånd anslutet med ledande ledningar, bildar en sluten krets i form av en rektangulär slinga..
När du skjuter stången, längden x ökar eller minskar, och därmed ändras slingans område, vilket är tillräckligt för att skapa ett variabelt flöde.
Som vi sa tidigare, om vinkeln mellan B och slingans normala ändras, fältflödet ändras enligt:
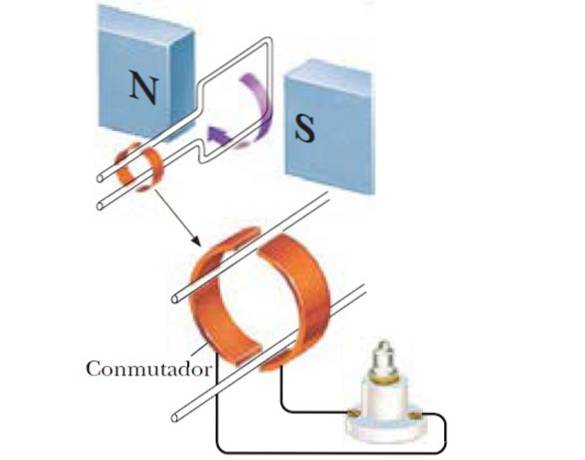
Sålunda erhålls en sinusformad generator, och om istället för en enda spole används ett antal N-spolar, är den inducerade emgen större:
En cirkulär spole med N-varv och radie R, roterar med vinkelfrekvensen ω mitt i ett magnetfält av storlek B. Hitta ett uttryck för den maximala emf som induceras i spolen.
Uttrycket för emf inducerad av rotation appliceras när spolen har N-varv, med vetskap om att:
-Spolens yta är A = πRtvå
-Vinkeln θ varierar som en funktion av tiden som θ = ωt
Det är viktigt att notera att först θ = ωt ersätts i Faradays lag och snart härleds med avseende på tid:
ε = -NBA (cos θ) '= -NB (πRtvå[cos (ωt)] '= NBω (πRtvå) synd (ωt)
Eftersom maximal emf begärs inträffar det när sin ωt = 1, så slutligen:
εmax = NBω (πRtvå)
Ingen har kommenterat den här artikeln än.