De Hookes lag påpekar att deformationen av ett elastiskt föremål är direkt proportionell mot den kraft som appliceras på det. Proportionalitetskonstanten beror på objektets natur, dess geometri och materialet med vilket det är tillverkat..
Alla material har elastiska egenskaper i mer eller mindre utsträckning, så de överensstämmer med Hookes lag så länge de återgår till sina ursprungliga dimensioner, när kraften upphör. Fjädrar och gummiband är bra exempel på föremål som uppfyller Hookes lag, men det är även stålstift som ingår i en bro.
Att ta en fjäder eller fjäder som ett exempel för att hålla den sträckt eller komprimerad är det nödvändigt att applicera en kraft vars storlek är F. Enligt Hookes lag kommer fjädern att uppleva en deformation x:
F ∝ x
Den konstanta proportionaliteten, som kallas en fjäder fjäderstyvhet konstant, betecknas som k, därför:
F = k⋅x
I enheterna i det internationella systemet är kraften i newton (N) och deformationen i meter (m). Fjäderkonstanten har därför enheterna N / m. Fjäderkonstanten representerar den kraft som måste appliceras för att deformera den med 1 m längd.
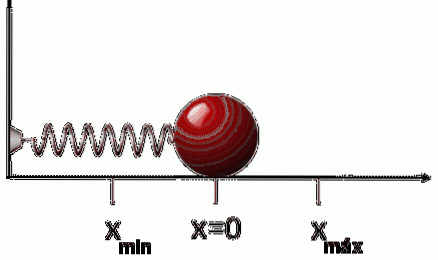
Om den, efter sträckning eller komprimering av fjädern, släpps, kommer den att röra sig i motsatt riktning till den applicerade kraften. Det betyder att om vi sträcker det komprimerar det och tvärtom. Därav styrkan FR Vad fjädern utövar det är:
FR = -k⋅x
Det negativa tecknet indikerar det ovan nämnda: att styrkan motsätter sig förskjutningen, därför är denna kraft känd som återställande kraft.
Artikelindex
Förhållandet mellan kraft och förskjutning under en vår upptäcktes av Robert Hooke (1635-1703), en anmärkningsvärd engelsk fysiker känd för sin rivalitet med Isaac Newton. Hooke var en mångsidig forskare som framgångsrikt vågade sig in i olika vetenskapsområden: mekanik, biologi, astronomi och arkitektur..
Hooke insåg att om kraften som appliceras på en fjäder inte är så stor, deformeras fjäderna proportionellt mot kraften, och när den kraften försvinner återgår fjädern till sin naturliga längd.
Således är Hookes lag i grafisk form i form av en rak linje vars lutning är fjäderkonstant. Följande bild visar den kraft som utövas på fjädern för att sträcka ut den - eller komprimera den - som en funktion av position x. Observera också att kraften inte beror på fjäderns naturliga längd utan på dess förskjutning..
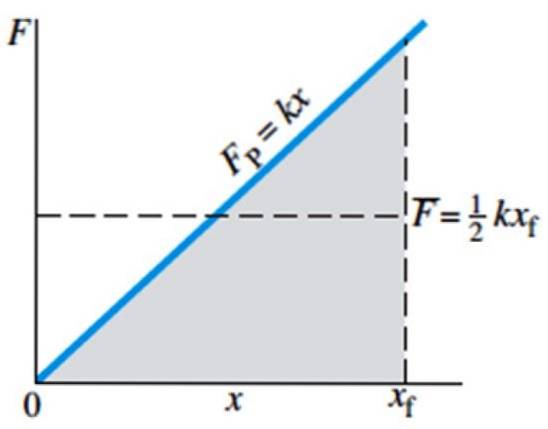
Medelkraften anges i diagrammet med stapeln F och är lika med ½ kxF, där xF är vårens slutposition.
Både den kraft som utövas på fjädern och den kraft den utövar på ett föremål som är knuten till den är variabla krafter. Ju mer du vill sträcka eller komprimera fjädern, desto mer kraft måste du använda för att uppnå den..
När en deformerande kraft appliceras på fjädern utförs arbete som lagras på våren och kan användas senare..
Mekaniskt arbete definieras som området under grafen för kraft F som en funktion av position x. För att beräkna arbetet W som en variabel kraft F (x) gör när ett objekt flyttas från position x1 upp till position xtvå vi måste beräkna den bestämda integralen:
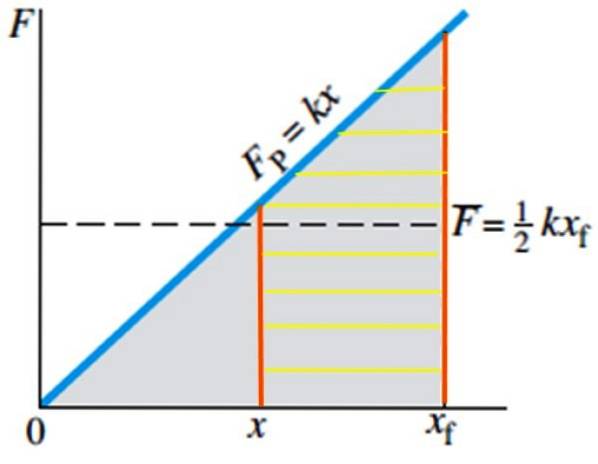
När det gäller arbetet som krävs för att föra en fjäder från dess jämviktsposition till position xF Det är väldigt enkelt, eftersom området som ska beräknas är det för den grå färgade triangeln i figur 4, vars formel är känd:
Area av triangeln = ½ bas. höjd
Därför är det nödvändiga arbetet:
W = ½ xF . (kxF) = ½ k (xF)två
Och om du vill beräkna det arbete som krävs för att föra fjädern från position x till position xF, skulle motsvara att beräkna ytan för den kläckta trapesformen i figur 5:
W = ½ k (xF)två - ½ k xtvå
Beroende på vilken applikation de är avsedda för kan fjädrarna vara spiralformade, cylindriska, koniska, spiralformiga, med ett cirkulärt tvärsnitt (den vanligaste), fyrkantiga eller rektangulära..
En klassificering som används i stor utsträckning är beroende på vilken typ av ansträngning de kommer att utsättas för: det finns vridnings-, flexions-, kompressions- och förlängningsfjädrar. De senare används i stor utsträckning och vissa fungerar lika för spänning och kompression..
Ett exempel på en tryckfjäder är den som används i leksaken pogo eller hoppstift. Dessa fjädrar lagrar mycket potentiell energi när de komprimeras och släpper ut den lite efterhand när de återgår till jämviktspositionen. På detta sätt är rebounds inte alltför plötsliga.
Trampolinfjädrar är förlängningsfjäder och tillverkas med tätt lindade spolar, med två krokar i ändarna. De kan behålla mycket potentiell energi, som de sedan släpper ut när någon klättrar upp och börjar hoppa på mattan, som också har sitt eget elastiska svar, som alla material..
Torsionsfjädrar är mycket vanliga eftersom de används för att göra klädnypor. Istället för krokar i ändarna böjer de sig i en vinkel för att motstå vridkrafter.
De mest lämpliga materialen för att tillverka fjädrar är de med en ultimat motstånd (slutligt motstånd) högt, det vill säga de stöder en stor ansträngning innan de går sönder. Det är också önskvärt att materialet har en hög sträckgräns så att det inte förlorar sina elastiska egenskaper med små ansträngningar..
Kraftiga fjädrar är tillverkade av legeringar inklusive högkolstål, koppar, nickel och brons.
Eftersom fjädrar har dygden att lagra potentiell energi när de sträcks eller komprimeras, kan de göra arbete genom att flytta saker som mekanismer..
På detta sätt har fjädrarna en mängd applikationer, från små och vardagliga föremål, via bilar, till maskiner av alla slag. Fjädrarna används för att:
-Dämpa vibrationer.
-Tillverkning utdragbara mekanismer: pennor, klädnypor, hårspännen.
-Gör fjädervåg eller dynamometrar
Och de är också en del av mekanismen för:
-Klockor.
-Trampoliner.
-Lås.
-Leksaker.
-Vapen.
-Nålmätare, till exempel galvanometern, används för att mäta strömmar, spänningar och motstånd.
En kraft av magneten 5,0 N appliceras på en fjäder, vilket får en längd på 3,5 cm att sträckas från sin naturliga längd..
a) Hur mycket sträcker det sig när den applicerade kraften är 7 N?
b) Hitta det arbete som utförts av den applicerade kraften för att sträcka fjädern 3,5 cm från sin naturliga längd.
Att veta att fjädern sträcks 3,5 cm genom att applicera 5,0 N kan vi beräkna dess konstant:
k = F / x = 5,0 N / 3,5 cm = 1,43 N / cm.
När en kraft på 7 N appliceras erhålls följande sträcka:
x = F / k = 7,0 N / 1,43 N / m = 4,9 cm
Arbetet som krävs för att deformera en fjäder ges av:
W = ½ kxtvå = 0,5 x 1,43 N / cm x (3,5 cm)två = 8,76 N. cm = 8,76 N. 1 x 10 -två m = 0,0876 J.
En fjäder med försumbar massa och 10 cm lång hängs upp från ett stöd. Om en massa på 2 kg hängs på den sträcks fjädern till 15 cm. Beräkna:
a) Fjäderkonstanten
b) Fjäderstorleken när en massa på 3 kg hängs upp.
Fjädersträckan är x = 15 - 10 cm = 5 cm
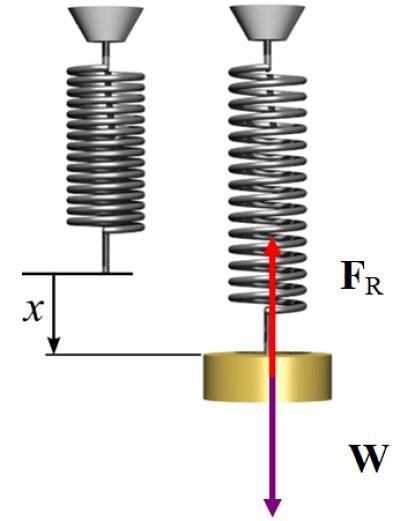
Eftersom systemet är i statisk jämvikt riktas fjäderns kraft vid sträckning vertikalt uppåt för att kompensera för vikten, som riktas nedåt, och sedan:
FR = W → kx = mg
k = 2 x 9,8 N / 5 x 10 -två m = 392 N / m
När en vikt på 3 kg är upphängd är den nya kraften W = 3 x 9,8 N = 29,4 N
I ett sådant fall är sträckan:
x = mg / k = 29. 4 N / 392 N / m = 0,075 m = 7,5 cm
Ingen har kommenterat den här artikeln än.