Blockera algebraelement, exempel, lösta övningar

De blockera algebra hänvisar till uppsättningen operationer som utförs genom block. Dessa och några andra element tjänar till att schematiskt representera ett system och enkelt visualisera dess svar på en given ingång..

I allmänhet innehåller ett system olika elektriska, elektroniska och elektromekaniska element, och var och en av dem, med sin respektive funktion och position i systemet, liksom hur de är relaterade, skisseras genom funktionella block.

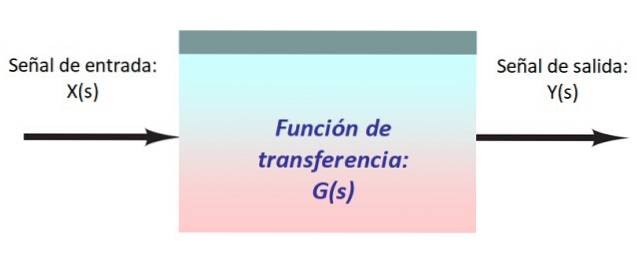
I figuren ovan finns ett mycket enkelt system, bestående av en insignal X (s), som kommer in i blocket med överföringsfunktionen G (s) som modifierar den och producerar utgången Y (s).

Det är bekvämt att representera signalerna och deras väg genom systemet med hjälp av pilar som går in och lämnar varje block. Vanligtvis riktas signalflödet från vänster till höger.

Fördelen med denna typ av schematisk är det visuella hjälpmedel som det ger för att förstå systemet, även om det inte är en fysisk representation av systemet. I själva verket är blockdiagrammet inte unikt, för beroende på synvinkeln kan flera diagram av samma system till och med ritas..

Det kan också hända att samma diagram tjänar flera system som inte nödvändigtvis är relaterade till varandra, så länge det adekvat beskriver deras beteende. Det finns olika system vars svar är lika i många avseenden, till exempel en LC-krets (induktorkondensator) och ett massfjädersystem..

Artikelindex

• 1 Vad är ett blockschema?
• 2 Delar av blockschemat
  • 2.1 Signalen
  • 2.2 Blocket
  • 2.3 Summa poäng
  • 2.4 Grenpunkt
• 3 Exempel på blockalgebraregler
  • 3.1 Kaskadblock
  • 3.2 Block parallellt
  • 3.3 Flytta en adderare åt vänster
  • 3.4 Flytta en adderare till höger
  • 3.5 Flytta en förgreningspunkt från vänster till höger
  • 3.6 Flytta en förgreningspunkt från höger till vänster
  • 3.7 Återkopplingssystem
  • 3.8 System med feedback och givare
• 4 Lösta övningar
  • 4.1 Övning 1
  • 4.2 Övning 2
• 5 Referenser

Vad är ett blockschema?

Systemen är i allmänhet mer komplicerade än den i figur 1, men blockalgebra ger en serie enkla regler för att manipulera systemschemat och reducera det till sin enklaste version..

Som förklarats i början använder diagrammet block, pilar och cirklar för att fastställa förhållandet mellan varje komponent i systemet och flödet av signaler som går igenom det..

Blockalgebra låter dig jämföra två eller flera signaler genom att addera, subtrahera och multiplicera dem, samt analysera det bidrag som varje komponent ger till systemet.

Tack vare detta är det möjligt att reducera hela systemet till en enda insignal, en enda överföringsfunktion som fullständigt beskriver systemets verkan och motsvarande utgång..

Blockdiagramelement

Elementen i blockschemat är som följer:

Signalen

Signalerna är av mycket varierande natur, till exempel är det vanligt att det är en elektrisk ström eller en spänning, men det kan vara ljus, ljud och mer. Det viktiga är att den innehåller information om ett visst system.

Signalen betecknas med stora bokstäver om det är en funktion av variabeln s av Laplace-transformationen: X (s) (se figur 1) eller med gemener om det är en funktion av tiden t, som x (t).

I blockschemat representeras ingångssignalen av en pil riktad mot blocket, medan utsignalen, betecknad Y (s) eller y (t), indikeras av en utgående pil.

Både ingångs- och utgångssignalerna är unika och riktningen som informationen flödar bestäms av pilens riktning. Och algebra är densamma för någon av de två variablerna.

Kvarteret

Blocket representeras av en kvadrat eller en rektangel (se figur 1) och kan användas för att utföra operationer eller implementera överföringsfunktionen, som vanligtvis betecknas med versalen G. Denna funktion är en matematisk modell som använder svaret erbjuds av systemet till en insignal.

Överföringsfunktionen kan uttryckas i termer av tid t som G (t) eller variabeln s som G (s).

När insignalen X (er) når blocket multipliceras den med överföringsfunktionen och transformeras till utsignalen Y (s). Matematiskt uttrycks det så här:

Y (s) = X (s). G (s)

På motsvarande sätt är överföringsfunktionen förhållandet mellan Laplace-transformation av utsignalen och Laplace-transformation av insignalen, förutsatt att systemets initiala förhållanden är noll:

G (s) = Y (s) / X (s)

Summa poäng

Tilläggspunkten, eller adderaren, symboliseras av en cirkel med ett kors inuti. Den används för att kombinera två eller flera signaler med hjälp av addition och subtraktion. I slutet av pilen som symboliserar tecknet placeras ett + -tecken direkt om nämnda tecken läggs till eller ett - tecken om det subtraheras..

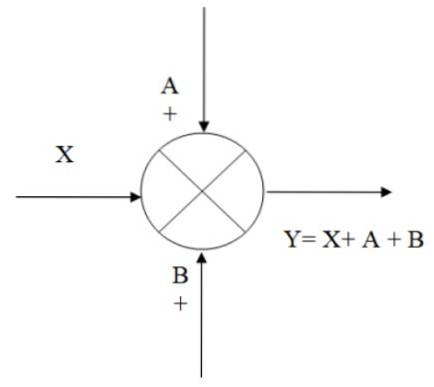
I följande figur finns ett exempel på hur adderaren fungerar: vi har ingångssignalen X, till vilken signalerna A och B läggs till, vilket resulterar i utgången Y, som är algebraiskt ekvivalent med:

Y = X + A + B

Grenpunkt

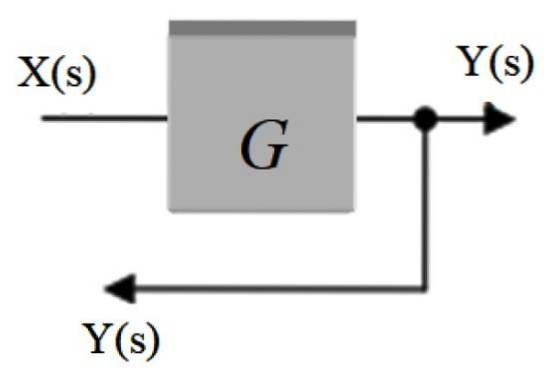
Det kallas också förgreningspunkt. I den distribueras signalen som kommer ut ur ett block till andra block eller till en adderare. Den representeras av en punkt placerad på signalpilen och en annan pil kommer ut ur den som omdirigerar signalen till en annan del.

Exempel på blockalgebraregler

Som förklarats tidigare är tanken att uttrycka systemet med hjälp av blockschemat och minska det för att hitta överföringsfunktionen som beskriver det. Följande är blockalgebra regler för att förenkla diagram:

Kaskad block

När du har en signal som passerar successivt genom G-blocken₁, G_två, G₃..., reduceras till ett enda block vars överföringsfunktion är produkten av G₁, G_två, G₃...

I följande exempel kommer signalen X (s) in i det första blocket och dess utgång är:

Y₁(s) = X (s) .G₁(s)

Vrid Y₁(s) ange block G_två(s), vars produktion är:

Y_två(s) = X (s) .G₁(s). G_två(s)

Proceduren är giltig för n kaskadblock:

Y_n (s) = X (s). G₁(s) .G_två(s) ... G_n(s)

Parallella block

I diagrammet till vänster förgrenar sig signalen X för att komma in i G-blocken₁(s) och G_två(s):

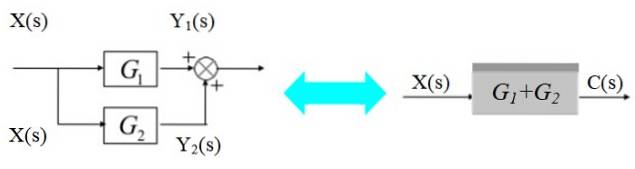
De respektive utsignalerna är:

Y₁(s) = X (s) .G₁(s)

Y_två(s) = X (s) .G_två(s)

Dessa signaler läggs samman för att erhålla:

C (s) = Y₁(s) + Y_två(s) = X (s). [G₁(s) + G_två(s)]

Som visas i diagrammet till höger.

Flytta en adderare åt vänster

En adderare kan flyttas till vänster om blocket enligt följande:

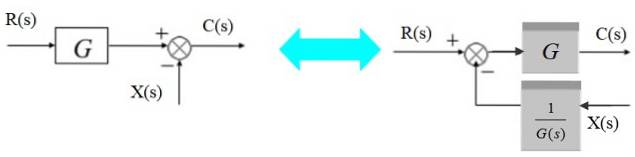
Till vänster är utsignalen:

C (s) = R (s). G (s) - X (s)

Motsvarande till höger:

C (s) = [R (s) - X (s) / G (s)]. G (s)

Flytta en adderare till höger

Adderaren kan flyttas till höger om blocket så här:

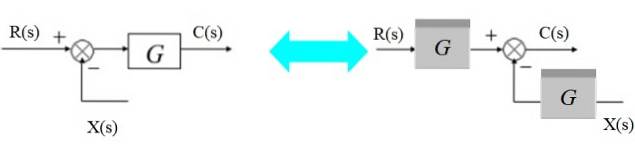
Till vänster har vi: [R (s) - X (s)]. G (s) = C (s)

Och till höger:

R (s). G (s) - X (s). G (s) = C (s)

Flytta en förgreningspunkt från vänster till höger

För att flytta förgreningspunkten från vänster till höger om blocket, observera bara att utgången C (s) till höger är produkten X (s) .G (s). Eftersom du vill konvertera den till X (s) igen, multiplicera med den inversa av G (s).

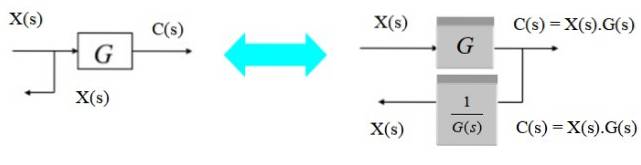
Flytta en förgreningspunkt från höger till vänster

Alternativt kan förgreningspunkten flyttas från höger till vänster enligt följande:

Eftersom vi vid utgången av grenen vill få C (s), sätter du helt enkelt in ett nytt block G (s) vid en grenpunkt till vänster om originalblocket.

Återkopplingssystem

I följande system matas utgångssignalen C (s) tillbaka genom adderaren till vänster:

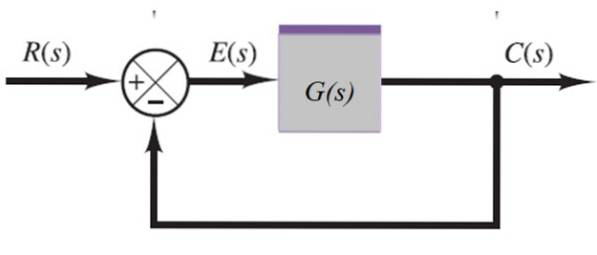
C (s) = E (s). G (s)

Men:

E (s) = R (s) -C (s)

Genom att ersätta detta uttryck i den föregående ekvationen förblir det: C (s) = [R (s) -C (s)]. G (s), från vilken C (s) kan lösas:

C (s) + C (s) .G (s) = R (s) .G (s) → C (s). [1 + G (s)] = R (s). G (s)

C (s) = R (s). G (s) / [1 + G (s)]

Eller alternativt:

C (s) / R (s) = G (s) / [1 + G (s)]

I grafisk form kvarstår det efter förenkling:

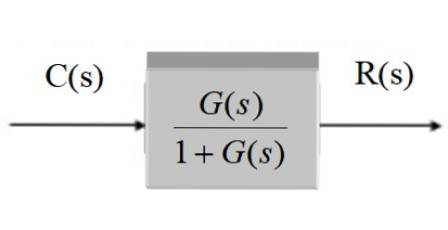
System med feedback och givare

Givaren består av överföringsfunktionen H (s):

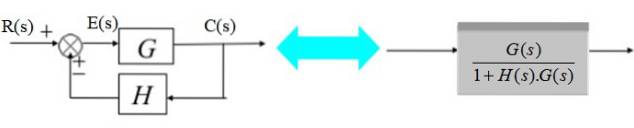
I diagrammet till höger är utsignalen C (s):

C (s) = E (s). G (s) med E (s) = R (s) - C (s). H (s)

Sedan:

C (s) = [R (s) - C (s). H (s)]. G (s)

C (s) [1+ H (s) .G (s)] = R (s) .G (s)

Därför kan C (s) lösas genom:

C (s) = G (s). R (s) / [1+ H (s) .G (s)]

Och överföringsfunktionen kommer att vara:

G (s) / [1+ H (s). G (s)]

Som visas i det förenklade diagrammet till höger.

Lösta övningar

Övning 1

Hitta överföringsfunktionen för följande system:

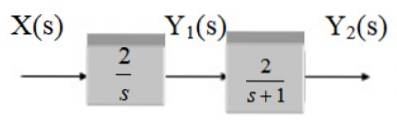
Lösning

Den behandlar två block i kaskad, därför är överföringsfunktionen produkten av funktionerna G₁ och G_två.

Det måste:

G₁ = 2 / s

G_två = 2 / (s + 1)

Därför är den eftersträvade överföringsfunktionen:

G (s) = 4 / [s (s + 1)]

Övning 2

Minska följande system:

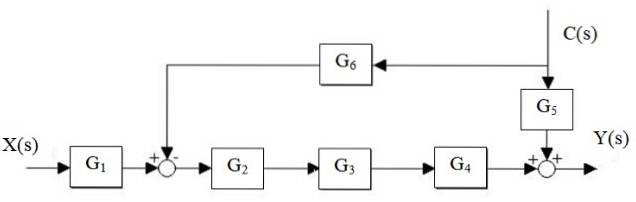
Lösning

Först reduceras G-kaskaden_två, G₃ och G_4, och parallellen G separeras₅ och G₆:

Sedan adderaren till vänster om block G_två ⋅G₃ ⋅ G₄ flyttar till höger:

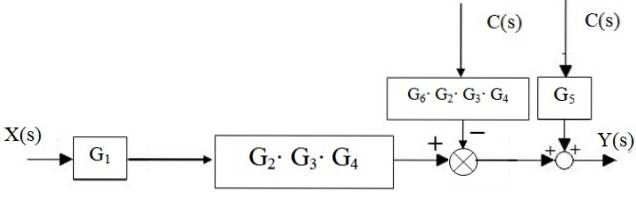
Tilläggarna till höger reduceras till bara en, liksom kaskadblocken:

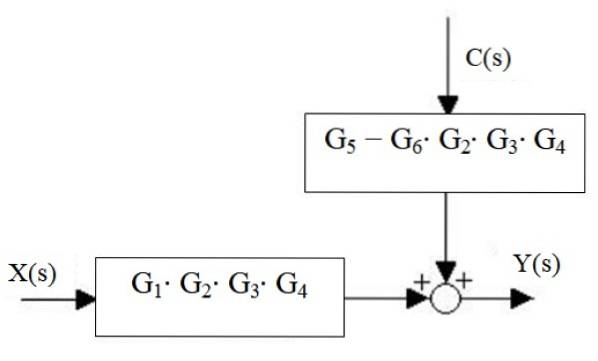
Slutligen är systemets utdata:

Y (s) = X (s) ⋅G₁⋅ G_två ⋅G₃ ⋅ G₄ + C (s) ⋅ [G₅ - G₆ ⋅ G_två ⋅G₃ ⋅ G₄]

Referenser

1. Alaydi, J. Kontrollsystems blockschema. Återställd från: site.iugaza.edu.ps.
2. Bolton, W. 2006. Kontrollteknik. 2: a. Utgåva. Alpha Omega.
3. Cwalinsky, J. Introduktion till systemblockalgebra. Återställd från: cedengineering.com.
4. Dademuchconnection. Blockdiagram. Återställd från: dademuch.com.
5. Ogata, K. 2010. Modern styrteknik. 5: e. Utgåva. Pearson.