De skalär storlek Det är den mängd som vi kan mäta av en viss egenskap som inte beror på dess riktning eller position i rymden. De vektor storlek är den mängd som vi kan mäta som beror på riktning eller position i rymden.
Till exempel kommer ett fordon som reser från Mexico City till Merida att resa en distans 1323 km (skalarstorlek) men kommer att ha en förflyttning 1007 km (vektorstorlek).
| Tecknad vektor | Scalars | |
|---|---|---|
| Definition | Mängd som har storlek och riktning. | Mängd som bara har storlek. |
| Belopp | Vektorsumma eller geometrisk resultant. | Aritmetisk summa. |
| Exempel | Förskjutning, hastighet, vikt, kraft. | Längd, hastighet, massa, densitet, temperatur. |
Vissa fysiska kvantiteter kan uttryckas med ett tal och dess motsvarande enhet. En skalär är en kvantitet som har en storlek men ingen riktning. Skalarstorlek hänvisar till mätningen som sådan.
När vi har två skalar av samma egenskap lägger de till aritmetiskt som vi normalt skulle göra. Till exempel: 2 kg äpplen plus 4 kg äpplen motsvarar totalt 6 kg.
Massa är egenskapen som mäter mängden materia i en kropp och också karakteriserar dess tröghetsegenskaper. Ju större massa, desto större måste kraften appliceras för att få den att accelerera. Det är en skalär kvantitet eftersom kroppens massa inte förändras med den riktningsförändring som kroppen kan uppleva..
Massan uttrycks i gram och dess multiplar och submultipler: milligram, kg, ton, etc..
Avståndet eller längden är mätningen som finns mellan två punkter. Det uttrycks i meter eller multiplar därav: millimeter, centimeter, kilometer etc. Det är en skalär storlek eftersom avståndet blir detsamma om vi mäter det från höger till vänster eller vice versa..
Hastighet är avståndet som ett objekt färdas under en given tid. Det är en skalär kvantitet, som i kombination med riktning utgör den vektormängd som vi känner som hastighet. Till exempel kommer en simmare som gör två pooler fram och tillbaka (50 mx 2 = 100 m) på 50 sekunder, har en hastighet på 100 m / 50 s = 2 m / s men hans hastighet är lika med noll eftersom han återvände till utgångspunkten.
Vektor är ordet som definierar en kvantitet som har både riktning och storlek. Vektorstorleken skulle vara hur mycket vektorn mäter.
En vektor representeras av en enda fet kursiv bokstav med en uppåtpil:
När vi vill beteckna vektorstorleken gör vi det med samma bokstav som vi använder för vektorn men i normal kursiv utan uppåtpilen eller innesluten mellan två vertikala staplar:
Summan av vektorer kräver en geometrisk behandling, där vektorerna representeras grafiskt och summan kommer att vara lika med en ny eller resulterande vektor, som börjar från den ursprungliga punkten till den slutliga punkten..
I denna mening är summan av vektorstorlekarna inte lika med den aritmetiska summan av skalarstorlekarna och beror på storleken på de involverade vektorerna och vinkeln de bildar med varandra. Till exempel, om ett fordon färdas 3 km österut och därefter norrut 3 km mer, kommer summan av vektorstorlekarna inte att vara 6 km utan 4,24 km.
En förskjutning är helt enkelt en förändring i positionen för en punkt. Det är det raka segmentet riktat från startpunkten till slutpunkten, även om banan är böjd. Det är en vektormängd eftersom vi måste uttrycka längden eller avståndet mellan de två punkterna och förändringens riktning.
Det är till exempel inte samma sak att säga att vi går 3 km österut än 3 km västerut; i båda fallen har vi samma storlek (3 km) men riktningarna är motsatta.
En kropps vikt är en vektormängd, det är den kraft som utövas på kroppen av jordens attraktion. Storleken på kroppens vikt (w) av deg m är lika med:
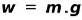
var g är storleken på accelerationen på grund av tyngdkraften, lika med 9,8 m / stvå. Vikt uttrycks i kraftenheter, Newton.
Hastighet är en fysisk kvantitet som anger avståndet som en partikel färdas i en given tid och riktning. Till exempel kommer en simmare som gör två pooler fram och tillbaka (50 m x 2 = 100 m) på 50 sekunder, har en hastighet som är lika med noll eftersom han återvände till startpunkten.
Du kanske är intresserad av att känna till skillnaderna mellan:
Ingen har kommenterat den här artikeln än.