
Youngs modulberäkning, applikationer, exempel, övningar
De Youngs modul o Elasticitetsmodul är den konstant som relaterar drag- eller kompressionsspänningen med respektive ökning eller minskning i längd för objektet som utsätts för dessa krafter.
Externa krafter som appliceras på föremål kan inte bara ändra deras rörelsetillstånd utan kan också ändra form eller till och med bryta eller bryta dem..

Youngs modul används för att studera de förändringar som produceras i ett material när en drag- eller tryckkraft appliceras externt. Det är mycket användbart i ämnen som teknik eller arkitektur.
Modellen har sitt namn till den brittiska forskaren Thomas Young (1773-1829), som var den som utförde studier av material som föreslog ett mått på styvheten hos olika material.
Artikelindex
- 1 Vad är Youngs modell?
- 2 Hur beräknas det?
- 2.1 Från ursprung till punkt A
- 2.2 Från A till B
- 2.3 Från B till C
- 2.4 Från C
- 2.5 Formler
- 2.6 Ekvation för att beräkna deformation
- 3 Exempel
- 4 Lösta övningar
- 4.1 Övning 1
- 4.2 Övning 2
- 5 Om Thomas Young
- 6 Referenser
Vad är Youngs modell?
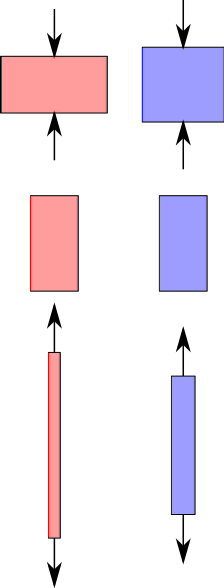
Hur mycket kan ett objekt deformeras? Detta är något som ingenjörer ofta vill veta. Svaret beror på materialets egenskaper och dimensionerna.
Du kan till exempel jämföra två stänger av aluminium med olika dimensioner. Var och en har olika tvärsnittsarea och längd och båda utsätts för samma dragkraft..
Det förväntade beteendet kommer att vara följande:
- Ju större tjocklek (tvärsnitt) av stången, desto mindre sträckning.
- Ju längre initiallängden är, desto större blir den slutliga sträckan.
Detta är vettigt, för trots allt visar erfarenheten att försöka deformera ett gummiband inte är detsamma som att försöka göra det med en stålstav..
En parameter som kallas materialets elasticitetsmodul är en indikation på dess elastiska respons.
Hur beräknas det?
Som läkare ville Young veta vilken roll artärernas elasticitet spelar för att blodcirkulationen ska fungera bra. Från sina erfarenheter drog han följande empiriska förhållande:
Spänningen är proportionell mot deformationen så länge materialets elastiska gräns inte överskrids.
Det är möjligt att grafiskt representera beteendet hos ett material vid applicering av en stress, som visas i följande bild.
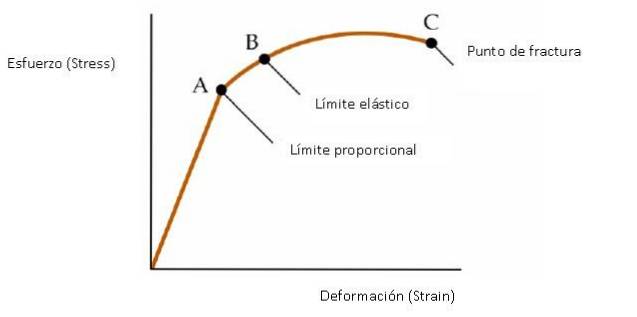
Från ursprung till punkt A
I det första avsnittet, som går från ursprung till punkt A, är grafen en rak linje. Hookes lag är giltig där:
F = kx
Var F är storleken på den kraft som återför materialet till sitt ursprungliga tillstånd, x är den deformation som den upplever och k är en konstant som beror på föremålet som utsätts för stress.
De här deformationerna är små och beteendet är helt elastiskt..
Från A till B
Från A till B uppträder materialet också elastiskt, men förhållandet mellan stress och belastning är inte längre linjärt.
Från B till C
Mellan punkterna B och C genomgår materialet en permanent deformation, eftersom det inte kan återgå till sitt ursprungliga tillstånd.
Från C
Om materialet fortsätter att sträcka sig från punkt C, går det så småningom sönder.
Matematiskt kan Youngs observationer sammanfattas enligt följande:
Stress ∝ Stam
Där proportionalitetskonstanten exakt är materialets elasticitetsmodul:
Stress = Elasticitetsmodul x Deformation
Det finns många sätt att deformera material. De tre vanligaste typerna av stress som ett objekt utsätts för är:
- Spänning eller stretching.
- Kompression.
- Klipp eller klipp.
En belastning som material ofta utsätts för, till exempel i civila konstruktioner eller bildelar, är dragkraft.
Formler
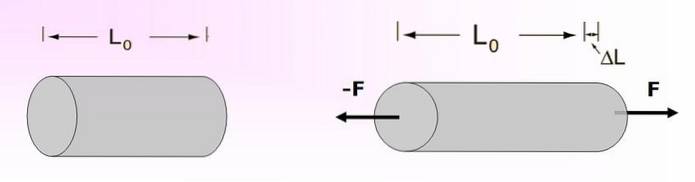
När ett objekt med längden L sträcks eller spänns utsätts det för ett drag som orsakar en variation i dess längd. Ett diagram över denna situation visas i figur 3.
Detta kräver att en kraft av storleken F appliceras per ytenhet till dess ändar för att orsaka sträckning, på ett sådant sätt att dess nya längd blir L + DL.
Ansträngningarna som görs för att deformera objektet kommer att vara just denna kraft per ytenhet, medan anstränga erfaren är ΔL / L.
Betecknar Youngs modul som Y, och enligt det ovan nämnda:
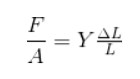
Svaret ligger i det faktum att töjningen anger töjningen relativt den ursprungliga längden. Det är inte samma sak som en bar på 1 m sträcker sig eller krymper 1 cm, en struktur med en längd på 100 meter deformeras också 1 cm.
För att delar och konstruktioner ska fungera korrekt finns det en tolerans beträffande tillåtna relativa deformationer.
Ekvation för att beräkna deformation
Om ovanstående ekvation analyseras enligt följande:
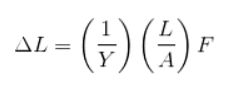
- Ju större tvärsnittsarea, desto mindre deformation.
- Ju längre längd desto större blir deformationen.
- Ju högre Youngs modul, desto lägre blir deformationen.
Enheter av stress motsvarar newton / kvadratmeter (N / mtvå). De är också enheterna för tryck, som i det internationella systemet bär namnet Pascal. Töjningen AL / L är å andra sidan dimensionell eftersom den är kvoten mellan två längder.
Enheterna i det engelska systemet är lb / in.två och de används också mycket ofta. Omvandlingsfaktorn för att gå från en till en annan är: 14,7 lb / in.två = 1.01325 x 105 Pa
Detta leder till att Youngs modul också har tryckenheter. Slutligen kan ovanstående ekvation uttryckas för att lösa Y:
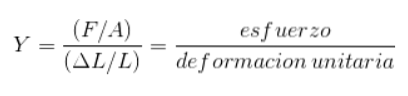
Inom materialvetenskapen är det elastiska svaret på dessa på olika ansträngningar viktigt för att välja det som är lämpligast för varje applikation, oavsett om det är tillverkning av en flygplansvinge eller ett billager. Egenskaperna hos det material som ska användas är avgörande för det svar som förväntas av det..
För att välja det bästa materialet är det nödvändigt att känna till de ansträngningar som en viss bit kommer att utsättas för; och välj därför det material som har de egenskaper som är mest i linje med designen.
Till exempel måste flygplanets vinge vara stark, lätt och flexibel. Materialen som används vid byggandet av byggnader måste till stor del motstå seismiska rörelser, men de måste också ha en viss flexibilitet.
Ingenjörer som konstruerar flygplansvingar, och även de som väljer byggmaterial, måste använda spänningsbelastningsdiagram som den som visas i figur 2..
Mätningar för att bestämma de mest relevanta elastiska egenskaperna hos ett material kan utföras i specialiserade laboratorier. Således finns det standardiserade tester som proverna utsätts för, på vilka olika spänningar appliceras, vilket senare mäter de resulterande deformationerna..
Exempel
Som redan nämnts ovan, Y beror inte på objektets storlek eller form utan på materialets egenskaper.
En annan mycket viktig anmärkning: för att ekvationen ovan ska vara tillämplig måste materialet vara isotrop, det vill säga dess egenskaper måste vara oförändrade under hela dess förlängning.
Inte alla material är isotropa: det finns sådana vars elastiska svar beror på vissa riktningsparametrar.
Deformationen som analyserats i de tidigare segmenten är bara en av många som ett material kan utsättas för. Exempelvis i termer av kompressionsspänning är det motsatsen till dragspänning.
De angivna ekvationerna gäller för båda fallen och nästan alltid värdena för Y är samma (isotropa material).
Ett anmärkningsvärt undantag är betong eller cement, som motstår kompression bättre än dragkraft. Därför måste den förstärkas när motstånd mot sträckning krävs. Stål är det material som anges för detta, eftersom det motstår sträckning eller dragning mycket bra..
Exempel på strukturer som utsätts för stress inkluderar att bygga pelare och bågar, klassiska byggnadselement i många gamla och moderna civilisationer..

Lösta övningar
Övning 1
En 2,0 m lång ståltråd i ett musikinstrument har en radie på 0,03 mm. När kabeln har en spänning på 90 N: hur mycket ändras dess längd?Faktum: Youngs modul av stål är 200 x 109 N / mtvå
Lösning
Det är nödvändigt att beräkna tvärsnittsarean A = πRtvå = π. (0,03 x 10-3 m)två = 2,83 x 10-9 mtvå
Stress är stress per ytenhet:

Eftersom repet är under spänning innebär det att det förlängs.
Den nya längden är L = L.eller + DL, där Leller är den ursprungliga längden:
L = 2,32 m
Övning 2
En marmorpelare vars tvärsnittsarea är 2,0 mtvå stöder en massa på 25 000 kg. Hitta:
a) Ansträngningen i ryggraden.
b) Sil.
c) Hur mycket förkortas kolonnen om dess höjd är 12 m?
Faktum: Youngs marmormodul är 50 x 109 N / mtvå
Lösning
a) Ansträngningen i kolonnen beror på vikten på 25000 kg:
P = mg = 25000 kg x 9,8 m / stvå = 245 000 N.
Därför är ansträngningen:
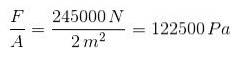
b) Töjningen är AL / L:
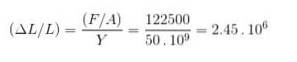
c) ΔL är variationen i längden, ges av:
AL = 2,45 x 10-6 x 12 m = 2,94 x 10-5 m = 0,0294 mm.
Marmorkolonnen förväntas inte krympa väsentligt. Observera att även om Youngs modul är lägre i marmor än i stål, och att pelaren också stöder en mycket större kraft, varierar dess längd nästan inte..
Å andra sidan, i repet i föregående exempel är variationen mycket mer märkbar, även om stålet har en mycket högre Young-modul.
Dess stora tvärsnittsarea griper in i kolonnen och är därför mycket mindre deformerbar.
Om Thomas Young

Elasticitetsmodulen är uppkallad efter Thomas Young (1773-1829), en mångsidig brittisk forskare som gjorde stora bidrag till vetenskapen på många områden.
Som fysiker studerade Young inte bara ljusets vågkaraktär som avslöjades av det berömda dubbelslitsexperimentet, utan han var också läkare, lingvist och hjälpte till och med att dechiffrera en del av de egyptiska hieroglyferna på den berömda Rosetta-stenen..
Han var medlem i Royal Society, Royal Swedish Academy of Sciences, American Academy of Arts and Sciences eller French Academy of Sciences, bland andra nobla vetenskapliga institutioner..
Det bör dock noteras att konceptet med modellen tidigare utvecklades av Leonhar Euler (1707-1873), och att forskare som Giordano Riccati (1709-1790) redan genomförde ett experiment som skulle ha genomfört Youngs modell i praktiken..
Referenser
- Bauer, W. 2011. Fysik för teknik och vetenskap. Volym 1. Mac Graw Hill. 422-527.
- Giancoli, D. 2006. Fysik: principer med tillämpningar. Sjätte upplagan. Prentice Hall. 238-249.



Ingen har kommenterat den här artikeln än.