Mått på position, central tendens och spridning

De mått på central tendens, spridning och position, är värden som används för att korrekt tolka en uppsättning statistiska data. Dessa kan bearbetas direkt, eftersom de erhålls från den statistiska studien, eller de kan organiseras i grupper av lika frekvens, vilket underlättar analysen..

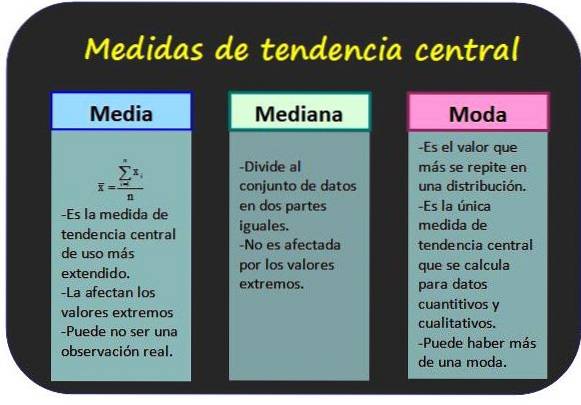
Mått på centrala tendenser

De gör det möjligt att veta vilka värden de statistiska uppgifterna är grupperade.

Aritmetiskt medelvärde

Det är också känt som medelvärdet av värdena för en variabel och erhålls genom att lägga till alla värden och dela resultatet med det totala antalet data.

• Aritmetiskt medelvärde för icke-grupperade data

Låt vara en variabel x som vi har n data utan att organisera eller gruppera, dess aritmetiska medel beräknas enligt följande:

Och i summeringsnotation:

Exempel

Ägarna till ett bergsturistjänst har för avsikt att veta hur många dagar i genomsnitt besökarna stannar i anläggningarna. För detta hölls ett register över varaktighetens dagar för 20 grupper av turister, med följande uppgifter:

1; 1; två; två; 1; 4; 5; 1; 3; 4; 5; 4; 3; 1; 1; två; två; 3; 4; 1

Det genomsnittliga antalet dagar som turister stannar är:

• Aritmetiskt medelvärde för grupperade data

Om variabelns data är organiserade i en tabell över absoluta frekvenser f_i och klasscentren är x₁, x_två,..., x_n, medelvärdet beräknas av:

Sammanfattningsnotation:

Median

Medianen för en grupp av n-värden för variabeln x är gruppens centrala värde, förutsatt att värdena ordnas i ökande ordning. På detta sätt är hälften av alla värden mindre än läget och den andra hälften är större..

• Median av icke-grupperade data

Följande fall kan uppstå:

-Antal n av värdena för variabeln x  udda: medianen är det värde som ligger mitt i värdegruppen:

-Antal n av värdena för variabeln x par: i detta fall beräknas medianen som genomsnittet av de två centrala värdena i datagruppen:

Exempel

För att hitta medianen för data från turisthemmet beställs de först från lägsta till högsta:

1; 1; 1; 1; 1; 1; 1; två; två; två; två; 3; 3; 3; 4; 4; 4; 4; 5; 5

Antalet data är jämnt, därför finns det två centrala data: X₁₀ och X_elva och eftersom båda är värda 2 är deras genomsnitt också.

Median = 2

• Median av samlade data

Följande formel används:

Symbolerna i formeln betyder:

-c: bredden på intervallet som innehåller medianen

-B_M: nedre gräns för samma intervall

-F_m: antal observationer som ingår i det intervall som medianen tillhör.

-n: totala data.

-F_BM: antal observationer innan av intervallet som innehåller medianen.

mode

Läget för icke-grupperade data är värdet med den högsta frekvensen, medan det för grupperade data är den klass med den högsta frekvensen. Mode anses vara den mest representativa data eller klass för distributionen.

Två viktiga kännetecken för detta mått är att en datamängd kan ha mer än ett läge och läget kan bestämmas för både kvantitativa och kvalitativa data..

Exempel

Fortsätt med informationen från turistparadorn, den som upprepas mest är 1, därför är det vanligaste att turister stannar 1 dag i parador.

Åtgärder för spridning

Mått på spridning beskriver hur grupperade uppgifterna är kring de centrala måtten.

Rang

Den beräknas genom att subtrahera de största och de minsta uppgifterna. Om denna skillnad är stor är det ett tecken på att data är spridda, medan små värden indikerar att data ligger nära medelvärdet..

Exempel

Räckvidden för data från turistparadorn är:

Område = 5−1 = 4

Variation

• Varians för icke-grupperade data

För att hitta variansen s^två Det krävs att man först känner till det aritmetiska medelvärdet, sedan beräknas den kvadratiska skillnaden mellan varje datastycke och medelvärdet, alla läggs till och divideras med det totala antalet observationer. Dessa skillnader är kända som avvikelser.

Variansen, som alltid är positiv (eller noll), anger hur långt observationerna är från medelvärdet: om variansen är hög är värdena mer spridda än när variansen är liten.

Exempel

Variansen för data från turisthemmet är:

1; 1; två; två; 1; 4; 5; 1; 3; 4; 5; 4; 3; 1; 1; två; två; 3; 4; 1

• Varians för grupperade data

För att hitta variansen för en grupperad datamängd krävs följande: i) medelvärdet, ii) frekvensen f_i  vilket är den totala datan i varje klass och iii) x_i  eller klassvärde:

Standardavvikelsen är den positiva kvadratroten av variansen, så den har en fördel framför variansen: den kommer i samma enheter som variabeln som studeras och därmed har du en mer direkt uppfattning om hur nära eller långt variabeln är från genomsnittet.

• Standardavvikelse för icke-grupperade data

Det bestäms helt enkelt genom att hitta kvadratroten av variansen för icke-grupperade data:

Standardavvikelsen för data från turisthemmet är:

s = √ (s^två) = √1.95 = 1.40

• Standardavvikelse för grupperade data

Det beräknas genom att hitta kvadratroten av variansen för grupperade data:

Positionsmätningar

Mätningar av position delar upp en ordnad uppsättning data i delar av samma storlek. Medianen, förutom att vara ett mått på central tendens, är också ett mått på position, eftersom det delar upp helheten i två lika delar. Men mindre delar kan erhållas med kvartiler, deciler och percentiler.

Kvartiler

Kvartilerna delar uppsättningen i fyra lika delar, var och en innehåller 25% av data. De betecknas som Q₁, F_två och Q₃ och medianen är kvartilen Q_två. På detta sätt ligger 25% av uppgifterna under Q-kvartilen.₁, 50% under Q-kvartilen_två eller median och 75% under Q-kvartilen₃.

• Kvartiler för icke-grupperade data

Data beställs och summan delas in i fyra grupper med samma antal data vardera. Positionen för den första kvartilen hittas av:

F₁ = (n + 1) / 4

Där n är den totala datan. Om resultatet är ett heltal lokaliseras data som motsvarar den positionen, men om det är decimalt, är det data som motsvarar heltalets medelvärde med nästa, eller för större precision interpoleras det linjärt mellan nämnda data.

Exempel

Positionen för den första kvartilen Q₁ för uppgifterna om turistparadoren är:

F₁ = (n + 1) / 4 = (20 + 1) / 4 = 5,25

Detta är positionen för kvartil 1 och eftersom resultatet är decimalt söks data X₅ och X_6, som är respektive X₅ = 1 och X₆ = 1 och är genomsnittliga, vilket resulterar i:

Första kvartilen = 1

1; 1; 1; 1; 1; 1; 1; två; två; två; två; 3; 3; 3; 4; 4; 4; 4; 5; 5.

Positionen för den andra kvartilen Q_två det är:

F_två = 2 (n + 1) / 4 = 10,5

Vad är genomsnittet mellan X₁₀ och X_elva och matchar medianen:

Andra kvartilen = Median = 2

Positionen för den tredje kvartilen beräknas av:

F₃ = 3 (n + 1) / 4 = 3 (20 + 1) / 4 = 15,75

Det är också decimal, därför är X ett medelvärde_femton och X₁₆:

1; 1; 1; 1; 1; 1; 1; två; två; två; två; 3; 3; 3; 4; 4; 4; 4; 5; 5.

Men eftersom båda är värda 4:

Tredje kvartilen = 4

Den allmänna formeln för placeringen av kvartiler i icke-grupperade data är:

F_k = k (n + 1) / 4

Med k = 1,2,3.

• Kvartiler för grupperade data

De beräknas på samma sätt som medianen:

Förklaringarna till symbolerna är:

-B_F: nedre gräns för intervallet som innehåller kvartilen

-c: bredden på det intervallet

-F_Vad: antal observationer som ingår i kvartilintervallet.

-n: totala data.

-F_BQ: antal data innan av intervallet som innehåller kvartilen.

Deciler och percentiler

Decilerna och percentilerna delar datauppsättningen i 10 lika delar och 100 lika delar respektive, och deras beräkning utförs på samma sätt som kvartilen.

• Deciler och percentiler för icke-grupperade data

Formlerna används respektive:

D_k = k (n + 1) / 10

Med k = 1,2,3 ... 9.

Decil D₅ måste vara lika med medianen.

P_k = k (n + 1) / 100

Med k = 1,2,3… 99.

P-percentilen_femtio måste vara lika med medianen.

Exempel

I exemplet med turisthemmet, D: s position₃ det är:

D₃ = 3 (20 + 1) / 10 = 6,3

Eftersom det är ett decimaltal beräknas X i genomsnitt₆ och X_7, båda lika med 1:

1; 1; 1; 1; 1; 1; 1; två; två; två; två; 3; 3; 3; 4; 4; 4; 4; 5; 5

Det betyder att 3 tiondelar av uppgifterna är under X₇ = 1 och de återstående ovan.

• Deciler och percentiler för grupperade data

Formlerna är analoga med dem för kvartiler. D används för att beteckna deciler och P för percentiler, och symbolerna tolkas på samma sätt:

Den empiriska regeln

När data distribueras symmetriskt och distributionen är unimodal finns det en regel som kallas  empirisk regel eller regel 68 - 95 - 99, som grupperar dem i följande intervall:

• 68% av uppgifterna ligger inom intervallet:

• 95% av uppgifterna ligger inom intervallet:

• 99% av uppgifterna ligger inom intervallet:

Exempel

I vilket intervall är 95% av uppgifterna från turistparadorn?

De ligger i intervallet: [2.5−1.40; 2,5 + 1,40] = [1,1; 3.9].

Referenser

1. Berenson, M. 1985. Statistik för management och ekonomi. Interamericana S.A.
2. Devore, J. 2012. Sannolikhet och statistik för teknik och vetenskap. 8: e. Utgåva. Cengage.
3. Levin, R. 1988. Statistik för administratörer. 2: a. Utgåva. Prentice hall.
4. Spiegel, M. 2009. Statistik. Schaum-serien. 4: e Utgåva. Mcgraw hill.
5. Walpole, R. 2007. Sannolikhet och statistik för teknik och vetenskap. Pearson.