
Dirac Jordan atommodellegenskaper och postulat

De Atommodell från Dirac-Jordanien är den relativistiska generaliseringen av den Hamilton-operatören i ekvationen som beskriver elektronens kvantvågfunktion. Till skillnad från den tidigare modellen, Schrodinger, är det inte nödvändigt att införa snurret med hjälp av Pauli-uteslutningsprincipen, eftersom det verkar naturligt.
Dessutom innehåller Dirac-Jordan-modellen relativistiska korrigeringar, spin-orbit-interaktionen och Darwin-termen, som står för den fina strukturen i atomens elektroniska nivåer..

Från och med 1928, forskarna Paul A. M. Dirac (1902-1984) och Pascual Jordan (1902-1980), planerade att generalisera den kvantmekanik som utvecklats av Schrodinger för att inkludera Einsteins korrigeringar av särskild relativitet..
Dirac startar från Schrodinger-ekvationen, som består av en differentiell operatör, kallad Hamiltonian, som arbetar med en funktion som kallas elektronvågfunktionen. Schrodinger tog dock inte hänsyn till de relativistiska effekterna.
Lösningarna för vågfunktionen tillåter oss att beräkna de regioner där elektronen kommer med en viss grad av sannolikhet att finnas runt kärnan. Dessa regioner eller zoner kallas orbitaler och beror på vissa diskreta kvantnummer, som definierar elektronens energi och vinkelmoment.
Artikelindex
- 1 Postulat
- 1.1 Diracs fyra postulat
- 2 Dirac-ekvationen
- 2.1 Dirac-Jordan-atomen
- 2.2 Relativistiska korrigeringar av energispektret
- 3 Intressanta artiklar
- 4 Referenser
Postulat
I kvantmekaniska teorier, oavsett om de är relativistiska eller inte, finns det inget begrepp om banor, eftersom varken elektronens position eller hastighet kan specificeras samtidigt. Och dessutom leder specificering av en av variablerna till total osäkerhet i den andra..
Hamiltonian är å sin sida en matematisk operatör som verkar på kvantvågfunktionen och är byggd från elektronens energi. Till exempel har en fri elektron total energi E som beror på dess linjära momentum sid Således:
E = (sidtvå) / 2m
För att konstruera Hamiltonian startar vi från detta uttryck och ersätter sid av kvantoperatören för fart:
sid = -i ħ ∂ / ∂r
Det är viktigt att notera att villkoren sid Y sid är olika, eftersom det första är fart och det andra är differentiell operatör associerad med fart.
Dessutom är jag den imaginära enheten och ħ Planck-konstanten dividerad med 2π, på detta sätt erhålls den Hamiltonian-operatören H för den fria elektronen:
H = (ħtvå/ 2m) ∂två / ∂rtvå
För att hitta Hamiltonens elektron i atomen, lägg till interaktionen mellan elektronen och kärnan:
H = (ħ2 / 2m) ∂två / ∂rtvå - eΦ (r)
I det föregående uttrycket -e är elektronens elektriska laddning och Φ (r) är den elektrostatiska potentialen som produceras av den centrala kärnan.
Nu agerar operatören H på vågfunktionen ψ enligt Schrodinger-ekvationen, som skrivs så här:
H ψ = (i ħ ∂ / ∂t) ψ
Diracs fyra postulat
Första postulatet: Den relativistiska vågekvationen har samma struktur som Schrodinger-vågekvationen, det som förändras är H:
H ψ = (i ħ ∂ / ∂t) ψ
Andra postulatet: Hamilton-operatören är konstruerad med utgångspunkt från Einsteins energimomentförhållande, som skrivs enligt följande:
E = (mtvå c4 + sidtvå ctvå)1/2
I det föregående förhållandet, om partikeln har momentum p = 0 så har vi den berömda ekvationen E = mctvå som relaterar restenergin för varje partikel med massa m till ljusets hastighet c.
Tredje postulatet: för att erhålla den Hamilton-operatören används samma kvantiseringsregel som används i Schrodinger-ekvationen:
sid = -i ħ ∂ / ∂r
I början var det inte klart hur man skulle hantera denna differentiella operatör som agerade inom en kvadratrot, så Dirac satte sig för att få en linjär Hamilton-operatör på momentoperatören och därifrån uppstod hans fjärde postulat.
Fjärde postulatet: för att bli av med kvadratroten i den relativistiska energiformeln föreslog Dirac följande struktur för Etvå:
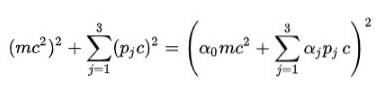
Naturligtvis är det nödvändigt att bestämma alfakoefficienterna (α0, α1, α2, α3) för att detta ska vara sant.
Diracs ekvation
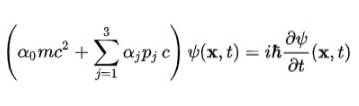
I sin kompakta form anses Dirac-ekvationen vara en av de vackraste matematiska ekvationerna i världen:
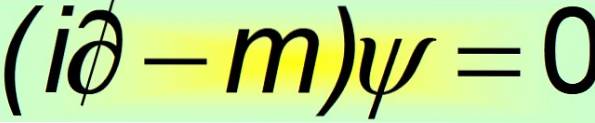
Och det är då det blir klart att den konstanta alfa inte kan vara skalära mängder. Det enda sättet att jämställdheten för det fjärde postulatet uppfylls är att de är 4 × 4 konstanta matriser, som är kända som Dirac-matriser:
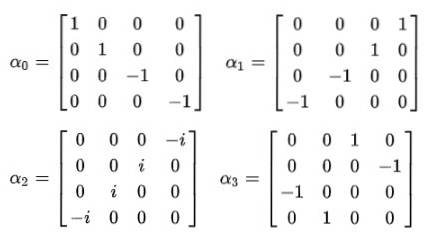
Det observeras omedelbart att vågfunktionen upphör att vara en skalarfunktion och blir en fyrkomponentsvektor som kallas spinor:
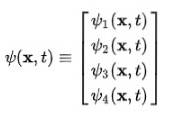
Dirac-Jordan-atomen
För att erhålla atommodellen är det nödvändigt att gå från ekvationen för den fria elektronen till den för elektronen i det elektromagnetiska fält som produceras av atomkärnan. Denna interaktion tas med i beräkningen genom att integrera den skalära potentialen Φ och vektorpotentialen TILL i Hamiltonian:
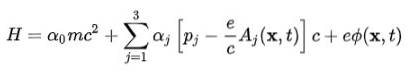
Vågfunktionen (spinor) som härrör från införandet av denna Hamilton har följande egenskaper:
- Den uppfyller speciell relativitet, eftersom den tar hänsyn till elektronens inneboende energi (första termen för den relativistiska Hamiltonian)
- Den har fyra lösningar som motsvarar de fyra komponenterna i spinor
- De två första lösningarna motsvarar en att snurra + ½ och den andra att snurra - ½
- Slutligen förutsäger de andra två lösningarna förekomsten av antimateria, eftersom de motsvarar positroner med motsatta snurr..
Den stora fördelen med Dirac-ekvationen är att korrigeringarna till grundläggande Schrodinger Hamiltonian H (o) kan delas upp i flera termer som vi kommer att visa nedan:
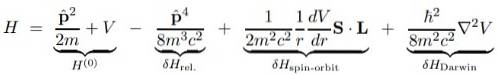
I det föregående uttrycket är V den skalära potentialen, eftersom vektorpotentialen TILL är noll om det centrala protonet antas vara stillastående och därför inte visas.
Anledningen till att Dirac-korrigeringarna till Schrodinger-lösningarna i vågfunktionen är subtila. De härrör från det faktum att de sista tre termerna för den korrigerade Hamiltonianen delas av ljusets hastighet c i kvadrat, ett enormt antal, vilket gör dessa termer numeriskt små.
Relativistiska korrigeringar av energispektret
Med hjälp av Dirac-Jordan-ekvationen hittar vi korrigeringar till elektronens energispektrum i väteatomen. Korrigeringar för energi i atomer med mer än en elektron i ungefärlig form finns också genom en metod som kallas störningsteori..
På liknande sätt tillåter Dirac-modellen att hitta den fina strukturkorrigeringen i vätgenerginivåer..
Emellertid erhålls ännu mer subtila korrigeringar som hyperfin struktur och Lamb shift från mer avancerade modeller som kvantfältsteori, som föddes just av bidrag från Dirac-modellen.
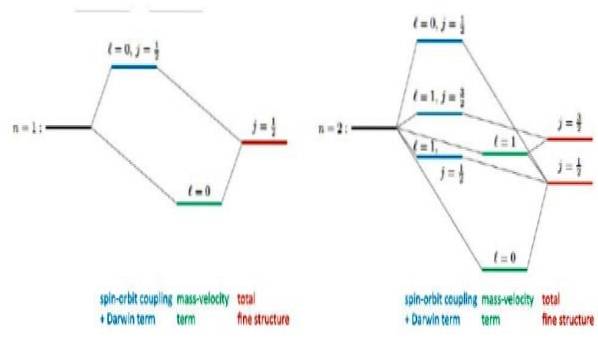
Följande bild visar hur Diracs relativistiska korrigeringar av energinivåer ser ut:
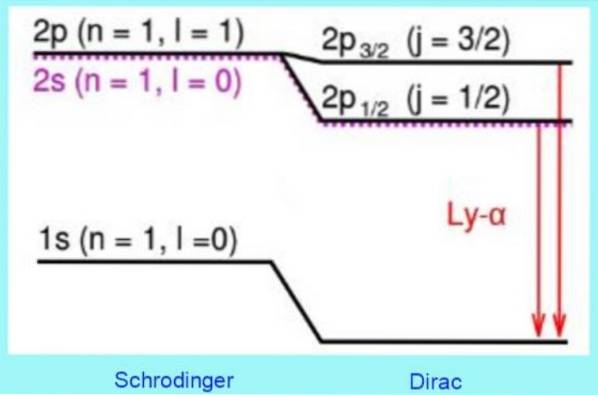
Exempelvis förutsäger lösningar på Dirac-ekvationen ett observerat skift på nivå 2s. Det är den välkända finstrukturkorrektionen i Lyman-alfa-linjen i vätespektrumet (se figur 3).
Förresten, den fina strukturen är namnet i atomfysiken för fördubbling av linjerna i atomens utsläppsspektrum, vilket är en direkt konsekvens av elektronisk snurrning..
Artiklar av intresse
Atomic de Broglie-modellen.
Chadwick Atomic Model.
Heisenberg atommodell.
Perrins atommodell.
Thomsons atommodell.
Dalton atommodell.
Schrödingers atommodell.
Atommodell för Democritus.
Atommodell av Leucippus.
Bohr atommodell.
Nuvarande atommodell.
Referenser
- Atomteori. Återställd från wikipedia.org.
- Elektronmagnetiskt ögonblick. Återställd från wikipedia.org.
- Quanta: En begreppshandbok. (1974). Oxford University Press. Återställd från Wikipedia.org.
- Dirac Jordan atommodell. Återställd från prezi.com.
- Det nya kvantuniverset. Cambridge University Press. Återställd från Wikipedia.org.



Ingen har kommenterat den här artikeln än.